Storyboard

Para descrever como o ângulo evolui ao longo do tempo, é necessário analisar sua variação ao longo do tempo.

A relação entre a variação do ângulo equivale ao ângulo do arco percorrido no tempo decorrido, que, ao dividir pelo tempo decorrido, torna-se a velocidade angular.

Quando se considera um intervalo de tempo finito, a velocidade angular representa a velocidade angular média durante esse intervalo.

>Modelo

ID:(611, 0)

Conceito

>Top

ID:(15409, 0)

Descrição

>Top

Uma vez introduzido o conceito de tempo decorrido, podemos definir o movimento em termos do ângulo percorrido. Para isso, devemos medir:

• o ângulo atual, que é determinado como diferença de ângulo em relação a uma origem a partir da qual estamos medindo;

• o ângulo inicial, que é determinado como diferença de ângulo em relação à mesma origem anterior e é calculado como a diferença entre o primeiro e o segundo.

ID:(12516, 0)

Conceito

>Top

A base da descrição de qualquer evolução é a definição do tempo em que esta é descrita. Em particular, trabalhamos com o tempo decorrido ($\Delta t$) a partir de um tempo de referência.

• No caso de um cronômetro, o tempo decorrido é medido a partir do início da medição, ou seja, um tempo inicial zero ($t_0=0$).

• No caso de um relógio, o tempo decorrido é medido a partir de um tempo inicial definido, que pode ser ou não zero.

ID:(12507, 0)

Conceito

>Top

Uma situação que pode surgir é quando a velocidade angular é constante, o que significa que o ângulo percorrido aumenta proporcionalmente ao tempo decorrido. Em outras palavras, usando , isso pode ser expresso como:

$\omega=\omega_0$

É importante observar que a velocidade angular é sempre medida em relação a um sistema de referência. Nesse caso, a velocidade angular constante é em relação ao sistema de referência sendo usado para medição.

ID:(11410, 0)

Descrição

>Top

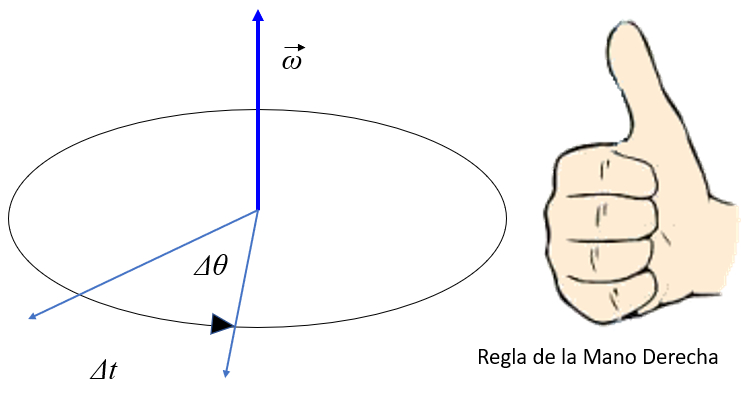
A velocidade angular média é definida como o ângulo percorrido no tempo decorrido. Como a rotação requer um eixo, este é desenhado de forma ortogonal ao disco que representa o corpo que gira. Para integrar o eixo, a velocidade angular é definida como um vetor em que a magnitude é o ângulo percorrido por unidade de tempo e a direção é definida em função da direção do eixo:

ID:(10967, 0)

Imagem

>Top

No caso de velocidade angular constante e tempo inicial conhecido, o ângulo pode ser calculado usando a seguinte fórmula:

A fórmula é representada graficamente abaixo:

Esta fórmula é útil para calcular o ângulo girado por um objeto em situações em que tanto a velocidade angular quanto o tempo inicial são conhecidos. A constância da velocidade angular indica que a magnitude da velocidade angular não muda com o tempo. O tempo inicial é a referência temporal a partir da qual o tempo decorrido é medido. Portanto, o ângulo girado pelo objeto pode ser calculado diretamente multiplicando a velocidade angular pelo tempo decorrido desde o tempo inicial.

ID:(11412, 0)

Descrição

>Top

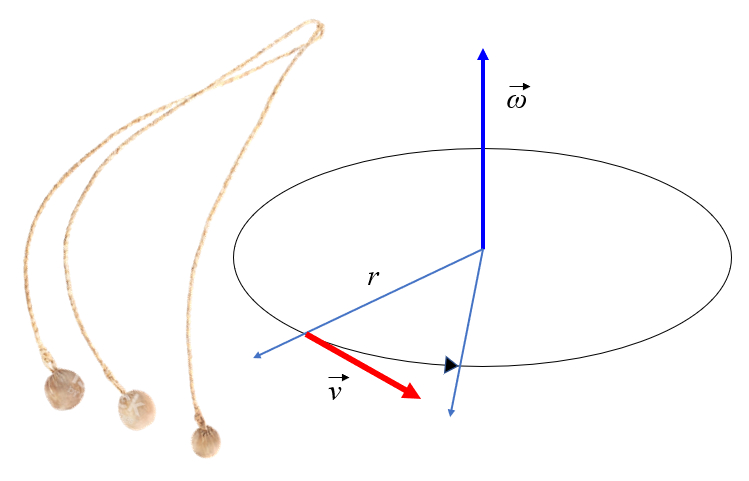
Se um objeto é submetido a um modo de manter um raio constante, ele irá girar conforme indicado na figura. Ao observar a figura, notará-se que a massa realiza um movimento de translação com uma velocidade tangencial que é igual ao raio multiplicado pela velocidade angular:

No entanto, se o elemento que conecta o objeto ao eixo for cortado, o objeto continuará a se mover tangencialmente em linha reta.

ID:(310, 0)

Imagem

>Top

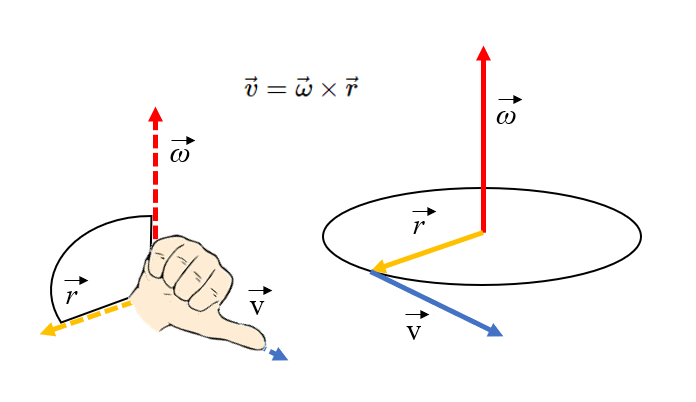
A orientação da velocidade tangencial pode ser obtida usando a regra da mão direita. Se os dedos apontam em direção ao eixo de rotação e são curvados em direção ao vetor de posição (raio), o polegar apontará na direção da velocidade tangencial:

ID:(11599, 0)

Conceito

>Top

Parâmetro selecionado

Cálculos

ID:(15420, 0)

Equação

>Top, >Modelo

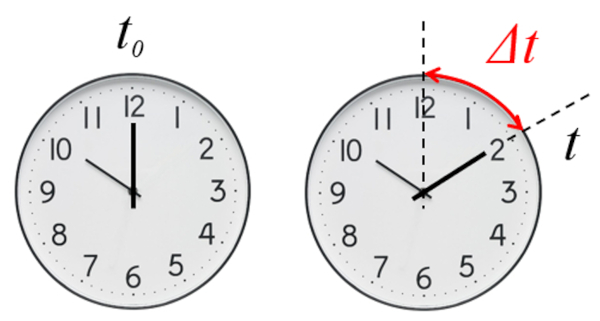
Para descrever a rotação de um objeto, precisamos determinar la variação de ângulo ($\Delta\theta$). Isso é feito subtraindo o ângulo inicial ($\theta_0$) do valor alcançado pelo objeto durante sua rotação, que é O ângulo ($\theta$):

$ \Delta\theta = \theta - \theta_0 $

Condições

Variáveis

$\theta$

Ângulo

$rad$

$\theta_0$

ângulo inicial

$rad$

$\Delta\theta$

Variação de ângulo

$rad$

Relação

ID:(3680, 0)

Equação

>Top, >Modelo

Para descrever o movimento de um objeto, precisamos calcular o tempo decorrido. Essa magnitude é obtida medindo o tempo inicial e o tempo final do movimento. A duração é determinada subtraindo o tempo inicial do tempo final.

Isso é representado matematicamente como

$ \Delta t \equiv t - t_0 $

Condições

Variáveis

$t$

Tempo

$s$

$\Delta t$

Tempo decorrido

$s$

$t_0$

Tempo inicial

$s$

Relação

onde $\Delta t$ é a duração, $t$ é o tempo final e $t_0$ é o tempo inicial.

ID:(4353, 0)

Equação

>Top, >Modelo

Para estimar o deslocamento de um objeto, é necessário conhecer sua la velocidade angular ($\omega$) em função de o tempo ($t$). Portanto, introduz-se a la velocidade angular média ($\bar{\omega}$), definida como a proporção entre la variação de ângulo ($\Delta\theta$) e o tempo decorrido ($\Delta t$).

Para medir isso, pode-se utilizar um sistema como o mostrado na imagem:

Para determinar a velocidade angular média, um elemento refletor é colocado no eixo ou em um disco com vários elementos refletores, e o movimento é registrado para estimar o comprimento do arco $\Delta s$ e o ângulo associado ao raio $r$. Em seguida, a diferença de tempo quando a marca passa diante do sensor é registrada como $\Delta t$. A velocidade angular média é determinada dividindo-se o ângulo percorrido pelo tempo decorrido.

A equação que descreve a velocidade angular média é:

$ \bar{\omega} \equiv\displaystyle\frac{ \Delta\theta }{ \Delta t }$

Condições

Variáveis

$\Delta\theta$

Diferença de ângulos

$rad$

$\Delta t$

Tempo decorrido

$s$

$\bar{\omega}$

Velocidade angular média

$rad/s$

Relação

Desenvolvimento

A definição de la velocidade angular média ($\bar{\omega}$) é considerada como la variação de ângulo ($\Delta\theta$),

$ \Delta\theta = \theta - \theta_0 $

e o tempo decorrido ($\Delta t$),

$ \Delta t \equiv t - t_0 $

A relação entre ambos é definida como la velocidade angular média ($\bar{\omega}$):

$ \bar{\omega} \equiv\displaystyle\frac{ \Delta\theta }{ \Delta t }$

Deve-se notar que a velocidade média é uma estimativa da velocidade angular real. O principal problema é que:

Se a velocidade angular varia durante o tempo decorrido, o valor da velocidade angular média pode ser muito diferente da velocidade angular média.

Portanto, a chave é:

Determinar a velocidade em um tempo decorrido suficientemente curto para minimizar sua variação.

ID:(3679, 0)

Equação

>Top, >Modelo

Quando a velocidade angular é constante, é trivial que a velocidade angular média seja igual a essa velocidade angular constante. Em outras palavras, la velocidade angular inicial ($\omega_0$) é igual a la velocidade angular média ($\bar{\omega}$):

$ \bar{\omega} = \omega_0 $

Condições

Variáveis

$\omega_0$

Velocidade angular inicial

$rad/s$

$ \bar{\omega}$

Velocidade angular média

$rad/s$

Relação

ID:(15431, 0)

Equação

>Top, >Modelo

No caso em que a velocidade angular é constante, la velocidade angular média ($\bar{\omega}$) coincide com o valor de la velocidade angular inicial ($\omega_0$), então

Nesse cenário, podemos calcular o ângulo percorrido em função do tempo lembrando que ele está associado à diferença entre os ângulos atual e inicial, bem como o tempo atual e o inicial. Portanto, o ângulo ($\theta$) é igual a o ângulo inicial ($\theta_0$), la velocidade angular inicial ($\omega_0$), o tempo ($t$) e o tempo inicial ($t_0$) conforme mostrado abaixo:

$ \theta = \theta_0 + \omega_0 ( t - t_0 )$

Condições

Variáveis

$\theta$

Ângulo

$rad$

$\theta_0$

ângulo inicial

$rad$

$t$

Tempo

$s$

$t_0$

Tempo inicial

$s$

$\omega_0$

Velocidade angular inicial

$rad/s$

Relação

Desenvolvimento

No caso em que la velocidade angular inicial ($\omega_0$) é igual a la velocidade angular média ($\bar{\omega}$),

$ \bar{\omega} = \omega_0 $

Portanto, com la diferença de ângulos ($\Delta\theta$), que é igual a o ângulo ($\theta$) dividido por o ângulo inicial ($\theta_0$), obtemos:

$ \Delta\theta = \theta - \theta_0 $

E com o tempo decorrido ($\Delta t$), que é igual a o tempo ($t$) dividido por o tempo inicial ($t_0$), obtemos:

$ \Delta t \equiv t - t_0 $

Podemos reescrever a equação para la velocidade angular média ($\bar{\omega}$) como:

$ \bar{\omega} \equiv\displaystyle\frac{ \Delta\theta }{ \Delta t }$

Isso pode ser expresso como:

$\omega_0 = \omega = \displaystyle\frac{\Delta\theta}{\Delta t} = \displaystyle\frac{\theta - \theta_0}{t - t_0}$

Ao resolver, obtemos:

$ \theta = \theta_0 + \omega_0 ( t - t_0 )$

A equação representa uma reta no espaço ângulo-tempo.

ID:(1023, 0)

Equação

>Top, >Modelo

Podemos calcular la distância percorrida em um tempo ($\Delta s$) a partir de la velocidade ($s_0$) y la posição ($s$) usando a seguinte equação:

$ \Delta s \equiv s - s_0 $

Condições

Variáveis

$\Delta s$

Distância percorrida em um tempo

$m$

$s$

Posição

$m$

$s_0$

Velocidade

$m$

Relação

ID:(4352, 0)

Equação

>Top, >Modelo

La velocidade média ($\bar{v}$) pode ser calculado a partir de la distância percorrida em um tempo ($\Delta s$) e o tempo decorrido ($\Delta t$) usando:

$ \bar{v} \equiv\displaystyle\frac{ \Delta s }{ \Delta t }$

Condições

Variáveis

$\Delta s$

Distância percorrida em um tempo

$m$

$\Delta t$

Tempo decorrido

$s$

$\bar{v}$

Velocidade média

$m/s$

Relação

ID:(3152, 0)

Equação

>Top, >Modelo

Quando a velocidade é constante, então trivialmente a velocidade média é igual a essa velocidade constante. Ou seja, la velocidade constante ($v_0$) é igual a la velocidade média ($\bar{v}$):

$ \bar{v} = v_0$

Condições

Variáveis

$v_0$

Velocidade constante

$m/s$

$\bar{v}$

Velocidade média

$m/s$

Relação

ID:(10276, 0)

Equação

>Top, >Modelo

A posição la distância percorrida em um tempo ($\Delta s$) em um movimento circular pode ser calculada a partir de la variação de ângulo ($\Delta\theta$) e o rádio ($r$) da órbita utilizando a seguinte fórmula:

$ \Delta s=r \Delta\theta $

Condições

Variáveis

$\Delta s$

Distância percorrida em um tempo

$m$

$r$

Rádio

0

$m$

$\Delta\theta$

Variação de ângulo

$rad$

Relação

Desenvolvimento

Se um objeto está a uma distância igual a o rádio ($r$) de um eixo e realiza uma rotação de uma variação de ângulo ($\Delta\theta$), que com o ângulo ($\theta$) e o ângulo inicial ($\theta_0$) é

$ \Delta\theta = \theta - \theta_0 $

ele terá percorrido um arco la distância percorrida em um tempo ($\Delta s$), que com la posição ($s$) e la velocidade ($s_0$) é

$ \Delta s \equiv s - s_0 $

Este arco pode ser calculado multiplicando o rádio ($r$) pelo ângulo, ou seja,

$ \Delta s=r \Delta\theta $

.

ID:(5302, 0)

Equação

>Top, >Modelo

Se dividirmos a relação entre la distância percorrida em um tempo ($\Delta s$) e o rádio ($r$) por la variação de ângulo ($\Delta\theta$),

e então dividirmos isso por o tempo decorrido ($\Delta t$), obtemos a relação que nos permite calcular la velocidade ($v$) ao longo da órbita, conhecida como velocidade tangencial, que está associada a la velocidade angular ($\omega$):

$ v_0 = r \omega $

$ v = r \omega $

Condições

Variáveis

$r$

Rádio

0

$m$

$v$

$v_0$

Velocidade constante

$m/s$

$\omega$

Velocidade angular

$rad/s$

Relação

Desenvolvimento

Como la velocidade média ($\bar{v}$) é com la distância percorrida em um tempo ($\Delta s$) e o tempo decorrido ($\Delta t$), igual a

$ \bar{v} \equiv\displaystyle\frac{ \Delta s }{ \Delta t }$

e com la distância percorrida em um tempo ($\Delta s$) expresso como arco de um círculo, e o rádio ($r$) e la variação de ângulo ($\Delta\theta$) são

$ \Delta s=r \Delta\theta $

e a definição de la velocidade angular média ($\bar{\omega}$) é

$ \bar{\omega} \equiv\displaystyle\frac{ \Delta\theta }{ \Delta t }$

então,

$v=\displaystyle\frac{\Delta s}{\Delta t}=r\displaystyle\frac{\Delta\theta}{\Delta t}=r\omega$

Como a relação é geral, pode ser aplicada para valores instantâneos, resultando em

$ v = r \omega $

ID:(3233, 0)