Velocidade angular constante, dois estágios
Storyboard
Se durante um movimento com velocidade angular constante ocorrer uma mudança nessa velocidade, isso resultará em um movimento que ocorre em duas etapas, cada uma caracterizada por uma velocidade angular definida.
Cada etapa é modelada com uma relação linear representada por uma reta, onde a chave está no fato de que o tempo e o ângulo final da primeira etapa são, por sua vez, o tempo e o ângulo inicial da segunda etapa.
É importante notar que este modelo apresenta um problema: a velocidade angular muda de forma instantânea, o que equivale a uma aceleração angular seguida de uma frenagem infinita, o que não é realista. No entanto, esse problema não é relevante se a duração das etapas for consideravelmente mais longa do que o tempo em que a mudança na velocidade angular ocorre.
ID:(1410, 0)
Mecanismos
Conceito
Mecanismos
ID:(15410, 0)
Conceito de dois estágios
Conceito
Um corpo pode se deslocar para la velocidade angular do primeiro estágio ($\omega_1$) e depois passar para uma la velocidade angular do segundo estágio ($\omega_2$). Com isso, entra em uma nova etapa, sendo necessário descrever ambas matematicamente para prever seu movimento.
A chave está em perceber que ambas as etapas têm um ponto em comum, caracterizado por:
• O ângulo final da primeira etapa e o início da segunda etapa, o primeiro ângulo final e segunda etapa começaram ($\theta_1$).
• O tempo final da primeira etapa e o início da segunda etapa, o tempo final da primeira e início da segunda etapa ($t_1$).
Assim, os diagramas do ângulo ao longo do tempo podem ser acoplados como na seguinte representação:
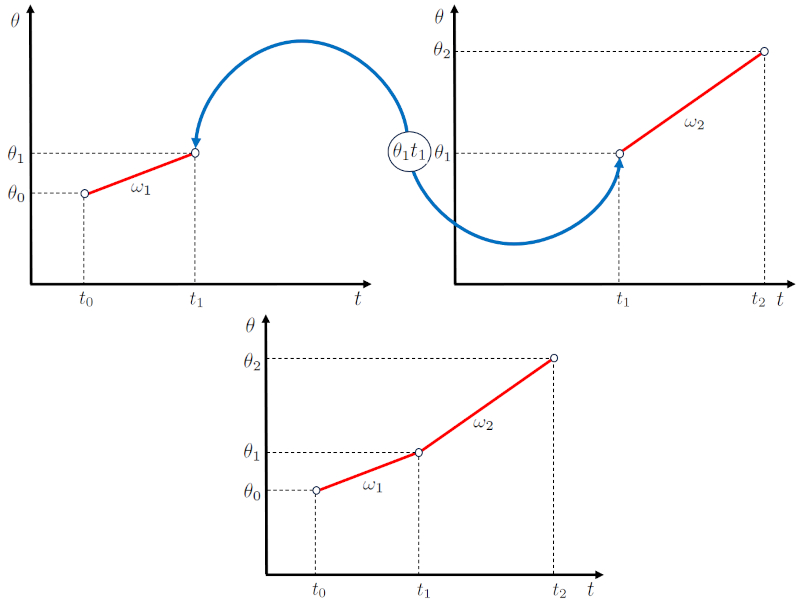
Nele, há um ponto inicial da primeira etapa caracterizado por o ângulo inicial ($\theta_0$) e o tempo inicial ($t_0$), e um ponto final da segunda etapa caracterizado por la ângulo final do segundo estágio ($\theta_2$) e o hora de término da segunda etapa ($t_2$).
ID:(12518, 0)
Velocidades angulares em dois estágios
Conceito
Em um cenário de movimento em duas etapas, primeiro o objeto avança um ângulo percorrido na primeira etapa ($\Delta\theta_1$) durante um tempo decorrido na primeira etapa ($\Delta t_1$) com uma velocidade angular do primeiro estágio ($\omega_1$).
Posteriormente, na segunda etapa, avança um ângulo percorrido na segunda etapa ($\Delta\theta_2$) durante um tempo gasto na segunda etapa ($\Delta t_2$) com uma velocidade angular do segundo estágio ($\omega_2$).
Ao representar isso graficamente, obtemos um diagrama de ângulo e tempo como mostrado abaixo:
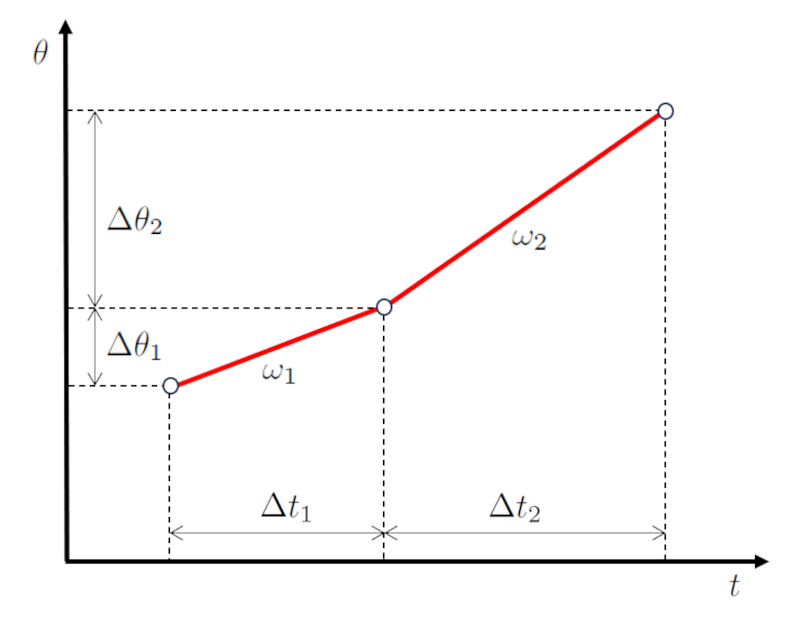
A chave aqui é que os valores o tempo decorrido na primeira etapa ($\Delta t_1$) e o tempo gasto na segunda etapa ($\Delta t_2$) são sequenciais, assim como os valores o ângulo percorrido na primeira etapa ($\Delta\theta_1$) e o ângulo percorrido na segunda etapa ($\Delta\theta_2$).
ID:(12525, 0)
Ângulos e tempos em duas etapas
Descrição
No caso de um movimento em duas etapas, a primeira etapa pode ser descrita por uma função que envolve os pontos o tempo inicial ($t_0$), o tempo final da primeira e início da segunda etapa ($t_1$), o ângulo inicial ($\theta_0$) e o primeiro ângulo final e segunda etapa começaram ($\theta_1$), representada por uma reta com inclinação de la velocidade angular do primeiro estágio ($\omega_1$):
Para a segunda etapa, definida pelos pontos o primeiro ângulo final e segunda etapa começaram ($\theta_1$), la ângulo final do segundo estágio ($\theta_2$), o tempo final da primeira e início da segunda etapa ($t_1$) e o hora de término da segunda etapa ($t_2$), é usada uma segunda reta com inclinação de la velocidade angular do segundo estágio ($\omega_2$):
que é representada como:
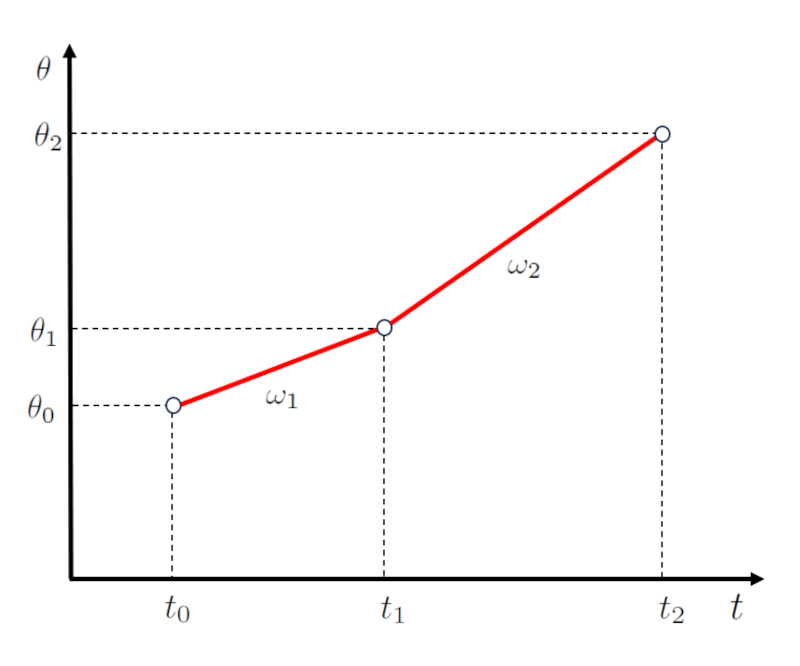
É importante notar que o início da segunda etapa, definido pelos pontos o tempo final da primeira e início da segunda etapa ($t_1$) e o primeiro ângulo final e segunda etapa começaram ($\theta_1$), coincide com o final da primeira etapa.
ID:(12517, 0)
Modelo
Conceito
Variáveis
Parâmetros
Parâmetro selecionado
Cálculos
Equação
$ \Delta t_1 \equiv t_1 - t_0 $
Dt = t - t_0
$ \Delta t_2 \equiv t_2 - t_1 $
Dt = t - t_0
$ \Delta\theta_1 = \theta_1 - \theta_0 $
Dtheta = theta - theta_0
$ \Delta\theta_2 = \theta_2 - \theta_1 $
Dtheta = theta - theta_0
$ \omega_1 \equiv\displaystyle\frac{ \Delta\theta_1 }{ \Delta t_1 }$
omega_m = Dtheta / Dt
$ \omega_2 \equiv\displaystyle\frac{ \Delta\theta_2 }{ \Delta t_2 }$
omega_m = Dtheta / Dt
$ \theta_1 = \theta_0 + \omega_1 ( t_1 - t_0 )$
theta = theta_0 + omega_0 * ( t - t_0 )
$ \theta_2 = \theta_1 + \omega_2 ( t_2 - t_1 )$
theta = theta_0 + omega_0 * ( t - t_0 )
$ v_1 = r \omega_1 $
v = r * omega
$ v_2 = r \omega_2 $
v = r * omega
ID:(15421, 0)
Diferença de ângulos (1)
Equação
Para descrever a rotação de um objeto, precisamos determinar la variação de ângulo ($\Delta\theta$). Isso é feito subtraindo o ângulo inicial ($\theta_0$) do valor alcançado pelo objeto durante sua rotação, que é O ângulo ($\theta$):
ID:(3680, 1)
Diferença de ângulos (2)
Equação
Para descrever a rotação de um objeto, precisamos determinar la variação de ângulo ($\Delta\theta$). Isso é feito subtraindo o ângulo inicial ($\theta_0$) do valor alcançado pelo objeto durante sua rotação, que é O ângulo ($\theta$):
ID:(3680, 2)
Tempo decorrido (1)
Equação
Para descrever o movimento de um objeto, precisamos calcular o tempo decorrido. Essa magnitude é obtida medindo o tempo inicial e o tempo final do movimento. A duração é determinada subtraindo o tempo inicial do tempo final.
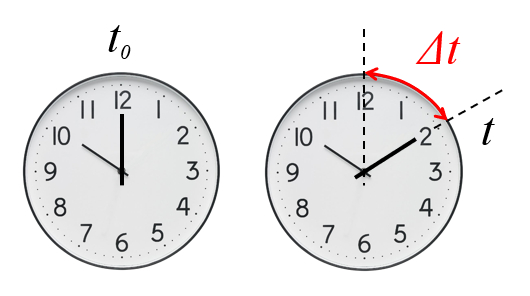
Isso é representado matematicamente como
onde $\Delta t$ é a duração, $t$ é o tempo final e $t_0$ é o tempo inicial.
ID:(4353, 1)
Tempo decorrido (2)
Equação
Para descrever o movimento de um objeto, precisamos calcular o tempo decorrido. Essa magnitude é obtida medindo o tempo inicial e o tempo final do movimento. A duração é determinada subtraindo o tempo inicial do tempo final.

Isso é representado matematicamente como
onde $\Delta t$ é a duração, $t$ é o tempo final e $t_0$ é o tempo inicial.
ID:(4353, 2)
Ângulo para velocidade angular constante (1)
Equação
No caso em que a velocidade angular é constante, la velocidade angular média ($\bar{\omega}$) coincide com o valor de la velocidade angular inicial ($\omega_0$), então
| $ \bar{\omega} = \omega_0 $ |
Nesse cenário, podemos calcular o ângulo percorrido em função do tempo lembrando que ele está associado à diferença entre os ângulos atual e inicial, bem como o tempo atual e o inicial. Portanto, o ângulo ($\theta$) é igual a o ângulo inicial ($\theta_0$), la velocidade angular inicial ($\omega_0$), o tempo ($t$) e o tempo inicial ($t_0$) conforme mostrado abaixo:
No caso em que la velocidade angular inicial ($\omega_0$) é igual a la velocidade angular média ($\bar{\omega}$),
| $ \bar{\omega} = \omega_0 $ |
Portanto, com la diferença de ângulos ($\Delta\theta$), que é igual a o ângulo ($\theta$) dividido por o ângulo inicial ($\theta_0$), obtemos:
| $ \Delta\theta = \theta - \theta_0 $ |
E com o tempo decorrido ($\Delta t$), que é igual a o tempo ($t$) dividido por o tempo inicial ($t_0$), obtemos:
| $ \Delta t \equiv t - t_0 $ |
Podemos reescrever a equação para la velocidade angular média ($\bar{\omega}$) como:
| $ \bar{\omega} \equiv\displaystyle\frac{ \Delta\theta }{ \Delta t }$ |
Isso pode ser expresso como:
$\omega_0 = \omega = \displaystyle\frac{\Delta\theta}{\Delta t} = \displaystyle\frac{\theta - \theta_0}{t - t_0}$
Ao resolver, obtemos:
| $ \theta = \theta_0 + \omega_0 ( t - t_0 )$ |
A equação representa uma reta no espaço ângulo-tempo.
ID:(1023, 1)
Ângulo para velocidade angular constante (2)
Equação
No caso em que a velocidade angular é constante, la velocidade angular média ($\bar{\omega}$) coincide com o valor de la velocidade angular inicial ($\omega_0$), então
| $ \bar{\omega} = \omega_0 $ |
Nesse cenário, podemos calcular o ângulo percorrido em função do tempo lembrando que ele está associado à diferença entre os ângulos atual e inicial, bem como o tempo atual e o inicial. Portanto, o ângulo ($\theta$) é igual a o ângulo inicial ($\theta_0$), la velocidade angular inicial ($\omega_0$), o tempo ($t$) e o tempo inicial ($t_0$) conforme mostrado abaixo:
No caso em que la velocidade angular inicial ($\omega_0$) é igual a la velocidade angular média ($\bar{\omega}$),
| $ \bar{\omega} = \omega_0 $ |
Portanto, com la diferença de ângulos ($\Delta\theta$), que é igual a o ângulo ($\theta$) dividido por o ângulo inicial ($\theta_0$), obtemos:
| $ \Delta\theta = \theta - \theta_0 $ |
E com o tempo decorrido ($\Delta t$), que é igual a o tempo ($t$) dividido por o tempo inicial ($t_0$), obtemos:
| $ \Delta t \equiv t - t_0 $ |
Podemos reescrever a equação para la velocidade angular média ($\bar{\omega}$) como:
| $ \bar{\omega} \equiv\displaystyle\frac{ \Delta\theta }{ \Delta t }$ |
Isso pode ser expresso como:
$\omega_0 = \omega = \displaystyle\frac{\Delta\theta}{\Delta t} = \displaystyle\frac{\theta - \theta_0}{t - t_0}$
Ao resolver, obtemos:
| $ \theta = \theta_0 + \omega_0 ( t - t_0 )$ |
A equação representa uma reta no espaço ângulo-tempo.
ID:(1023, 2)
Velocidade angular média (1)
Equação
Para estimar o deslocamento de um objeto, é necessário conhecer sua la velocidade angular ($\omega$) em função de o tempo ($t$). Portanto, introduz-se a la velocidade angular média ($\bar{\omega}$), definida como a proporção entre la variação de ângulo ($\Delta\theta$) e o tempo decorrido ($\Delta t$).
Para medir isso, pode-se utilizar um sistema como o mostrado na imagem:
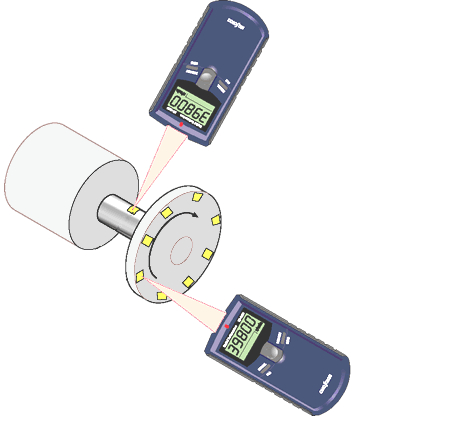
Para determinar a velocidade angular média, um elemento refletor é colocado no eixo ou em um disco com vários elementos refletores, e o movimento é registrado para estimar o comprimento do arco $\Delta s$ e o ângulo associado ao raio $r$. Em seguida, a diferença de tempo quando a marca passa diante do sensor é registrada como $\Delta t$. A velocidade angular média é determinada dividindo-se o ângulo percorrido pelo tempo decorrido.
A equação que descreve a velocidade angular média é:
A definição de la velocidade angular média ($\bar{\omega}$) é considerada como la variação de ângulo ($\Delta\theta$),
| $ \Delta\theta = \theta - \theta_0 $ |
e o tempo decorrido ($\Delta t$),
| $ \Delta t \equiv t - t_0 $ |
A relação entre ambos é definida como la velocidade angular média ($\bar{\omega}$):
| $ \bar{\omega} \equiv\displaystyle\frac{ \Delta\theta }{ \Delta t }$ |
Deve-se notar que a velocidade média é uma estimativa da velocidade angular real. O principal problema é que:
Se a velocidade angular varia durante o tempo decorrido, o valor da velocidade angular média pode ser muito diferente da velocidade angular média.
Portanto, a chave é:
Determinar a velocidade em um tempo decorrido suficientemente curto para minimizar sua variação.
ID:(3679, 1)
Velocidade angular média (2)
Equação
Para estimar o deslocamento de um objeto, é necessário conhecer sua la velocidade angular ($\omega$) em função de o tempo ($t$). Portanto, introduz-se a la velocidade angular média ($\bar{\omega}$), definida como a proporção entre la variação de ângulo ($\Delta\theta$) e o tempo decorrido ($\Delta t$).
Para medir isso, pode-se utilizar um sistema como o mostrado na imagem:

Para determinar a velocidade angular média, um elemento refletor é colocado no eixo ou em um disco com vários elementos refletores, e o movimento é registrado para estimar o comprimento do arco $\Delta s$ e o ângulo associado ao raio $r$. Em seguida, a diferença de tempo quando a marca passa diante do sensor é registrada como $\Delta t$. A velocidade angular média é determinada dividindo-se o ângulo percorrido pelo tempo decorrido.
A equação que descreve a velocidade angular média é:
A definição de la velocidade angular média ($\bar{\omega}$) é considerada como la variação de ângulo ($\Delta\theta$),
| $ \Delta\theta = \theta - \theta_0 $ |
e o tempo decorrido ($\Delta t$),
| $ \Delta t \equiv t - t_0 $ |
A relação entre ambos é definida como la velocidade angular média ($\bar{\omega}$):
| $ \bar{\omega} \equiv\displaystyle\frac{ \Delta\theta }{ \Delta t }$ |
Deve-se notar que a velocidade média é uma estimativa da velocidade angular real. O principal problema é que:
Se a velocidade angular varia durante o tempo decorrido, o valor da velocidade angular média pode ser muito diferente da velocidade angular média.
Portanto, a chave é:
Determinar a velocidade em um tempo decorrido suficientemente curto para minimizar sua variação.
ID:(3679, 2)
Velocidade e velocidade angular (1)
Equação
Se dividirmos a relação entre la distância percorrida em um tempo ($\Delta s$) e o rádio ($r$) por la variação de ângulo ($\Delta\theta$),
| $ \Delta s=r \Delta\theta $ |
e então dividirmos isso por o tempo decorrido ($\Delta t$), obtemos a relação que nos permite calcular la velocidade ($v$) ao longo da órbita, conhecida como velocidade tangencial, que está associada a la velocidade angular ($\omega$):
Como la velocidade média ($\bar{v}$) é com la distância percorrida em um tempo ($\Delta s$) e o tempo decorrido ($\Delta t$), igual a
| $ \bar{v} \equiv\displaystyle\frac{ \Delta s }{ \Delta t }$ |
e com la distância percorrida em um tempo ($\Delta s$) expresso como arco de um círculo, e o rádio ($r$) e la variação de ângulo ($\Delta\theta$) são
| $ \Delta s=r \Delta\theta $ |
e a definição de la velocidade angular média ($\bar{\omega}$) é
| $ \bar{\omega} \equiv\displaystyle\frac{ \Delta\theta }{ \Delta t }$ |
então,
$v=\displaystyle\frac{\Delta s}{\Delta t}=r\displaystyle\frac{\Delta\theta}{\Delta t}=r\omega$
Como a relação é geral, pode ser aplicada para valores instantâneos, resultando em
| $ v = r \omega $ |
ID:(3233, 1)
Velocidade e velocidade angular (2)
Equação
Se dividirmos a relação entre la distância percorrida em um tempo ($\Delta s$) e o rádio ($r$) por la variação de ângulo ($\Delta\theta$),
| $ \Delta s=r \Delta\theta $ |
e então dividirmos isso por o tempo decorrido ($\Delta t$), obtemos a relação que nos permite calcular la velocidade ($v$) ao longo da órbita, conhecida como velocidade tangencial, que está associada a la velocidade angular ($\omega$):
Como la velocidade média ($\bar{v}$) é com la distância percorrida em um tempo ($\Delta s$) e o tempo decorrido ($\Delta t$), igual a
| $ \bar{v} \equiv\displaystyle\frac{ \Delta s }{ \Delta t }$ |
e com la distância percorrida em um tempo ($\Delta s$) expresso como arco de um círculo, e o rádio ($r$) e la variação de ângulo ($\Delta\theta$) são
| $ \Delta s=r \Delta\theta $ |
e a definição de la velocidade angular média ($\bar{\omega}$) é
| $ \bar{\omega} \equiv\displaystyle\frac{ \Delta\theta }{ \Delta t }$ |
então,
$v=\displaystyle\frac{\Delta s}{\Delta t}=r\displaystyle\frac{\Delta\theta}{\Delta t}=r\omega$
Como a relação é geral, pode ser aplicada para valores instantâneos, resultando em
| $ v = r \omega $ |
ID:(3233, 2)
