Aceleração angular constante, dois estágios
Storyboard 
No caso de um movimento angular acelerado em duas etapas, no momento em que se passa da primeira para a segunda aceleração angular, a velocidade angular final da primeira etapa se torna a velocidade angular inicial da segunda. O mesmo ocorre com o ângulo, onde o ângulo final da primeira etapa é igual ao ângulo inicial da segunda etapa.
Ao contrário do modelo de duas velocidades angulares, este modelo não apresenta problemas de descontinuidade, exceto que a aceleração angular pode mudar de forma abrupta, o que é tecnicamente possível, embora muitas vezes não seja muito realista.
ID:(1409, 0)
Aceleração angular constante, dois estágios
Storyboard 
No caso de um movimento angular acelerado em duas etapas, no momento em que se passa da primeira para a segunda aceleração angular, a velocidade angular final da primeira etapa se torna a velocidade angular inicial da segunda. O mesmo ocorre com o ângulo, onde o ângulo final da primeira etapa é igual ao ângulo inicial da segunda etapa. Ao contrário do modelo de duas velocidades angulares, este modelo não apresenta problemas de descontinuidade, exceto que a aceleração angular pode mudar de forma abrupta, o que é tecnicamente possível, embora muitas vezes não seja muito realista.
Variáveis
Cálculos
Cálculos
Equações
A defini o da acelera o angular m dia baseada no ngulo percorrido
e no tempo decorrido
A rela o entre os dois definida como a acelera o angular m dia
dentro desse intervalo de tempo.
A defini o da acelera o angular m dia baseada no ngulo percorrido
e no tempo decorrido
A rela o entre os dois definida como a acelera o angular m dia
dentro desse intervalo de tempo.
Dado que la aceleração média ($\bar{a}$) igual a la diferença de velocidade ($\Delta v$) e o tempo decorrido ($\Delta t$) conforme
e la aceleração angular média ($\bar{\alpha}$) igual a la diferença de velocidades angulares ($\Delta\omega$) e o tempo decorrido ($\Delta t$) conforme
deduz-se que
$\bar{a}=\displaystyle\frac{\Delta v}{\Delta t}=r\displaystyle\frac{\Delta\omega}{\Delta t}=\bar{\alpha}$
Assumindo que la aceleração angular média ($\bar{\alpha}$) igual a la aceleração angular constante ($\alpha_0$)
e supondo que la aceleração média ($\bar{a}$) igual a la aceleração constante ($a_0$)
obt m-se a seguinte equa o:
Dado que la aceleração média ($\bar{a}$) igual a la diferença de velocidade ($\Delta v$) e o tempo decorrido ($\Delta t$) conforme
e la aceleração angular média ($\bar{\alpha}$) igual a la diferença de velocidades angulares ($\Delta\omega$) e o tempo decorrido ($\Delta t$) conforme
deduz-se que
$\bar{a}=\displaystyle\frac{\Delta v}{\Delta t}=r\displaystyle\frac{\Delta\omega}{\Delta t}=\bar{\alpha}$
Assumindo que la aceleração angular média ($\bar{\alpha}$) igual a la aceleração angular constante ($\alpha_0$)
e supondo que la aceleração média ($\bar{a}$) igual a la aceleração constante ($a_0$)
obt m-se a seguinte equa o:
Se assumirmos que la aceleração angular média ($\bar{\alpha}$) constante, equivalente a la aceleração angular constante ($\alpha_0$), ent o a seguinte equa o se aplica:
Portanto, considerando la diferença de velocidades angulares ($\Delta\omega$) junto com la velocidade angular ($\omega$) e la velocidade angular inicial ($\omega_0$):
e o tempo decorrido ($\Delta t$) em rela o a o tempo ($t$) e o tempo inicial ($t_0$):
a equa o para la aceleração angular média ($\bar{\alpha}$):
pode ser expressa como:
$\alpha_0 = \alpha = \displaystyle\frac{\Delta \omega}{\Delta t} = \displaystyle\frac{\omega - \omega_0}{t - t_0}$
Resolvendo isso, obtemos:
Se assumirmos que la aceleração angular média ($\bar{\alpha}$) constante, equivalente a la aceleração angular constante ($\alpha_0$), ent o a seguinte equa o se aplica:
Portanto, considerando la diferença de velocidades angulares ($\Delta\omega$) junto com la velocidade angular ($\omega$) e la velocidade angular inicial ($\omega_0$):
e o tempo decorrido ($\Delta t$) em rela o a o tempo ($t$) e o tempo inicial ($t_0$):
a equa o para la aceleração angular média ($\bar{\alpha}$):
pode ser expressa como:
$\alpha_0 = \alpha = \displaystyle\frac{\Delta \omega}{\Delta t} = \displaystyle\frac{\omega - \omega_0}{t - t_0}$
Resolvendo isso, obtemos:
No caso de la aceleração angular constante ($\alpha_0$), la velocidade angular ($\omega$) como fun o de o tempo ($t$) segue uma rela o linear com o tempo inicial ($t_0$) e la velocidade angular inicial ($\omega_0$) na forma:
Dado que o deslocamento angular igual rea sob a curva de velocidade angular-tempo, neste caso, pode-se adicionar as contribui es do ret ngulo:
$\omega_0(t-t_0)$
e do tri ngulo:
$\displaystyle\frac{1}{2}\alpha_0(t-t_0)^2$
Isso nos leva express o para o ângulo ($\theta$) e o ângulo inicial ($\theta_0$):
No caso de la aceleração angular constante ($\alpha_0$), la velocidade angular ($\omega$) como fun o de o tempo ($t$) segue uma rela o linear com o tempo inicial ($t_0$) e la velocidade angular inicial ($\omega_0$) na forma:
Dado que o deslocamento angular igual rea sob a curva de velocidade angular-tempo, neste caso, pode-se adicionar as contribui es do ret ngulo:
$\omega_0(t-t_0)$
e do tri ngulo:
$\displaystyle\frac{1}{2}\alpha_0(t-t_0)^2$
Isso nos leva express o para o ângulo ($\theta$) e o ângulo inicial ($\theta_0$):
Se resolvermos o tempo na equa o de la velocidade angular ($\omega$) que inclui as vari veis la velocidade angular inicial ($\omega_0$), o tempo ($t$), o tempo inicial ($t_0$) e la aceleração angular constante ($\alpha_0$):
obtemos a seguinte express o para o tempo:
$t - t_0 = \displaystyle\frac{\omega - \omega_0}{\alpha_0}$
Esta solu o pode ser substitu da na equa o para calcular o ângulo ($\theta$) usando o ângulo inicial ($\theta_0$) da seguinte forma:
o que resulta na seguinte equa o:
Se resolvermos o tempo na equa o de la velocidade angular ($\omega$) que inclui as vari veis la velocidade angular inicial ($\omega_0$), o tempo ($t$), o tempo inicial ($t_0$) e la aceleração angular constante ($\alpha_0$):
obtemos a seguinte express o para o tempo:
$t - t_0 = \displaystyle\frac{\omega - \omega_0}{\alpha_0}$
Esta solu o pode ser substitu da na equa o para calcular o ângulo ($\theta$) usando o ângulo inicial ($\theta_0$) da seguinte forma:
o que resulta na seguinte equa o:
Exemplos
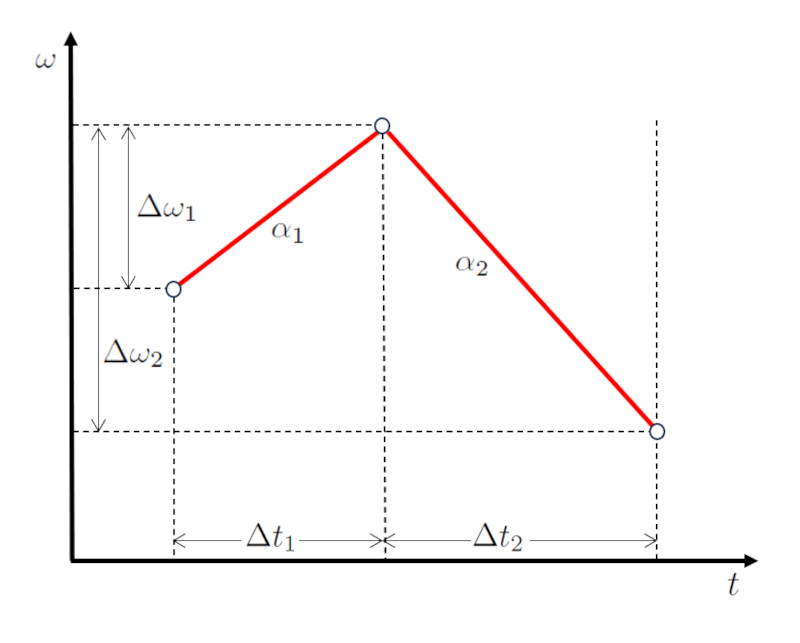
Em um cen rio de movimento em duas etapas, inicialmente o objeto ajusta sua velocidade pela diferen a de la variação das velocidades angulares no primeiro estágio ($\Delta\omega_1$) durante um per odo de o tempo decorrido na primeira etapa ($\Delta t_1$), experimentando uma acelera o de la aceleração angular durante o primeiro estágio ($\alpha_1$).
Na segunda etapa, o objeto continua modificando sua velocidade por la variação das velocidades angulares no segundo estágio ($\Delta\omega_2$) ao longo de um intervalo de tempo o tempo gasto na segunda etapa ($\Delta t_2$), com uma acelera o de la aceleração angular durante o segundo estágio ($\alpha_2$).
Ao visualizar isso graficamente, obt m-se um diagrama de velocidade versus tempo como mostrado abaixo:
importante notar que os intervalos de tempo o tempo decorrido na primeira etapa ($\Delta t_1$) e o tempo gasto na segunda etapa ($\Delta t_2$) s o sequenciais, assim como as diferen as de velocidade la variação das velocidades angulares no primeiro estágio ($\Delta\omega_1$) e la variação das velocidades angulares no segundo estágio ($\Delta\omega_2$).
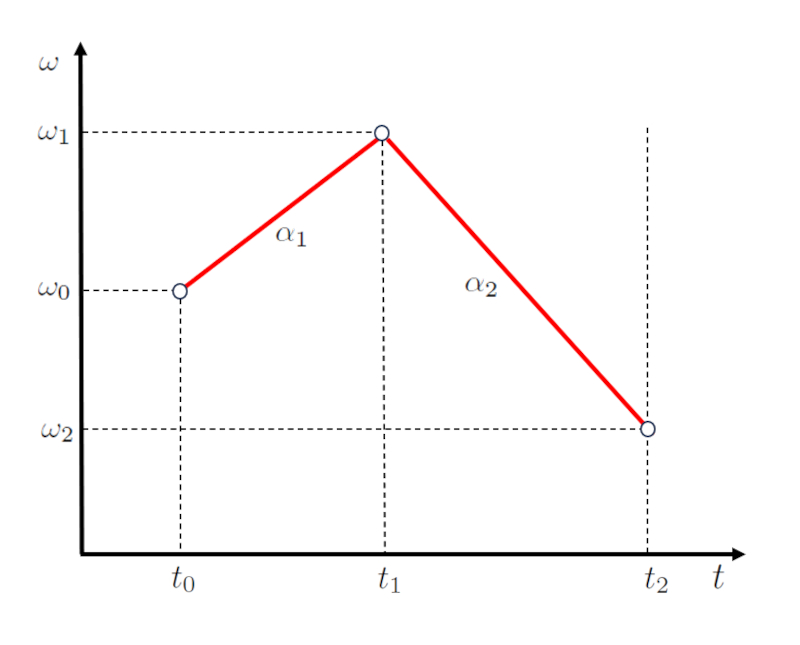
Na an lise de um movimento segmentado em duas etapas, a primeira fase caracterizada por uma fun o linear que incorpora os pontos o tempo inicial ($t_0$), o tempo final da primeira e início da segunda etapa ($t_1$), la velocidade angular inicial ($\omega_0$) e la primeira velocidade angular final e início do segundo estágio ($\omega_1$). Esta expressa atrav s de uma linha com inclina o de la aceleração angular durante o primeiro estágio ($\alpha_1$), cuja rela o matem tica especificada na seguinte equa o:
Na transi o para a segunda etapa, que definida pelos pontos la primeira velocidade angular final e início do segundo estágio ($\omega_1$), la velocidade angular final do segundo estágio ($\omega_2$), o tempo final da primeira e início da segunda etapa ($t_1$) e o hora de término da segunda etapa ($t_2$), adota-se uma nova fun o linear com uma inclina o de la aceleração angular durante o segundo estágio ($\alpha_2$). Esta rela o delineada pela segunda equa o apresentada:
A representa o gr fica destas rela es lineares ilustrada abaixo, fornecendo uma visualiza o clara de como a inclina o varia entre as duas etapas:
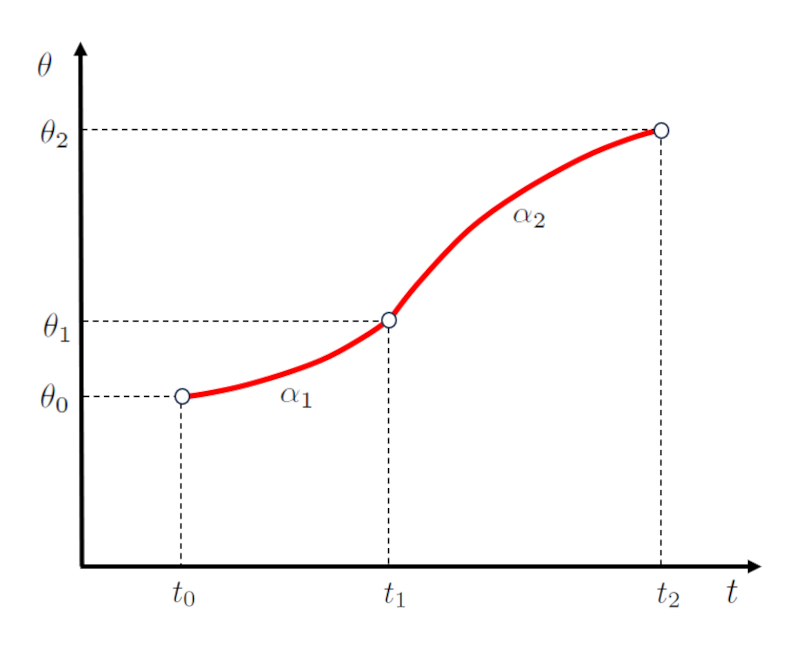
Em um cen rio de movimento dividido em duas etapas, o ngulo no final da primeira etapa o mesmo que o ngulo no in cio da segunda etapa, designado como o primeiro ângulo final e segunda etapa começaram ($\theta_1$).
Da mesma forma, o momento em que a primeira etapa termina coincide com o in cio da segunda etapa, marcado por o tempo final da primeira e início da segunda etapa ($t_1$).
Dado que o movimento definido pela acelera o angular experimentada, a velocidade angular no final da primeira etapa deve coincidir com a velocidade angular inicial da segunda etapa, indicada por la primeira velocidade angular final e início do segundo estágio ($\omega_1$).
No contexto de uma acelera o angular constante, o ngulo em o primeiro ângulo final e segunda etapa começaram ($\theta_1$) determinado pelas vari veis o ângulo inicial ($\theta_0$), la velocidade angular inicial ($\omega_0$), la aceleração angular durante o primeiro estágio ($\alpha_1$), o tempo final da primeira e início da segunda etapa ($t_1$) e o tempo inicial ($t_0$), conforme mostrado na seguinte equa o:
Na segunda etapa, o ngulo em la ângulo final do segundo estágio ($\theta_2$) calculado com base em o primeiro ângulo final e segunda etapa começaram ($\theta_1$), la primeira velocidade angular final e início do segundo estágio ($\omega_1$), la aceleração angular durante o segundo estágio ($\alpha_2$), o tempo final da primeira e início da segunda etapa ($t_1$) e o hora de término da segunda etapa ($t_2$), de acordo com:
A representa o gr fica dessas rela es ilustrada abaixo:
A taxa na qual a velocidade angular varia ao longo do tempo definida como la aceleração angular média ($\bar{\alpha}$). Para medi-la, necess rio observar la diferença de velocidades angulares ($\Delta\omega$) e o tempo decorrido ($\Delta t$).
A equa o que descreve la aceleração angular média ($\bar{\alpha}$) a seguinte:
A taxa na qual a velocidade angular varia ao longo do tempo definida como la aceleração angular média ($\bar{\alpha}$). Para medi-la, necess rio observar la diferença de velocidades angulares ($\Delta\omega$) e o tempo decorrido ($\Delta t$).
A equa o que descreve la aceleração angular média ($\bar{\alpha}$) a seguinte:
Para descrever a rota o de um objeto, precisamos determinar la variação de ângulo ($\Delta\theta$). Isso feito subtraindo o ângulo inicial ($\theta_0$) do valor alcan ado pelo objeto durante sua rota o, que o ângulo ($\theta$):
Para descrever a rota o de um objeto, precisamos determinar la variação de ângulo ($\Delta\theta$). Isso feito subtraindo o ângulo inicial ($\theta_0$) do valor alcan ado pelo objeto durante sua rota o, que o ângulo ($\theta$):
A acelera o definida como a varia o da velocidade angular por unidade de tempo.
Portanto, a acelera o angular la diferença de velocidades angulares ($\Delta\omega$) pode ser expressa em termos da velocidade angular la velocidade angular ($\omega$) e do tempo la velocidade angular inicial ($\omega_0$) da seguinte forma:
A acelera o definida como a varia o da velocidade angular por unidade de tempo.
Portanto, a acelera o angular la diferença de velocidades angulares ($\Delta\omega$) pode ser expressa em termos da velocidade angular la velocidade angular ($\omega$) e do tempo la velocidade angular inicial ($\omega_0$) da seguinte forma:
Para descrever o movimento de um objeto, precisamos calcular o tempo decorrido ($\Delta t$). Essa magnitude obtida medindo o tempo inicial ($t_0$) e o o tempo ($t$) desse movimento. A dura o determinada subtraindo o tempo inicial do tempo final:
Para descrever o movimento de um objeto, precisamos calcular o tempo decorrido ($\Delta t$). Essa magnitude obtida medindo o tempo inicial ($t_0$) e o o tempo ($t$) desse movimento. A dura o determinada subtraindo o tempo inicial do tempo final:
Com la aceleração angular constante ($\alpha_0$), la velocidade angular ($\omega$) forma uma rela o linear com o tempo ($t$), incorporando as vari veis la velocidade angular inicial ($\omega_0$) e o tempo inicial ($t_0$) da seguinte forma:
Esta equa o representa uma linha reta no plano de velocidade angular versus tempo.
Com la aceleração angular constante ($\alpha_0$), la velocidade angular ($\omega$) forma uma rela o linear com o tempo ($t$), incorporando as vari veis la velocidade angular inicial ($\omega_0$) e o tempo inicial ($t_0$) da seguinte forma:
Esta equa o representa uma linha reta no plano de velocidade angular versus tempo.
Dado que o deslocamento total corresponde rea sob a curva de velocidade angular versus tempo, no caso de uma aceleração angular constante ($\alpha_0$), determina-se que o deslocamento o ângulo ($\theta$) com as vari veis o ângulo inicial ($\theta_0$), o tempo ($t$), o tempo inicial ($t_0$) e la velocidade angular inicial ($\omega_0$) o seguinte:
Essa express o corresponde forma geral de uma par bola.
Dado que o deslocamento total corresponde rea sob a curva de velocidade angular versus tempo, no caso de uma aceleração angular constante ($\alpha_0$), determina-se que o deslocamento o ângulo ($\theta$) com as vari veis o ângulo inicial ($\theta_0$), o tempo ($t$), o tempo inicial ($t_0$) e la velocidade angular inicial ($\omega_0$) o seguinte:
Essa express o corresponde forma geral de uma par bola.
No caso de la aceleração angular constante ($\alpha_0$), a fun o de la velocidade angular ($\omega$) em rela o a o tempo ($t$), juntamente com as vari veis adicionais la velocidade angular inicial ($\omega_0$) e o tempo inicial ($t_0$), expressa pela equa o:
A partir desta equa o, poss vel calcular a rela o entre o ângulo ($\theta$) e o ângulo inicial ($\theta_0$), bem como a mudan a na velocidade angular:
No caso de la aceleração angular constante ($\alpha_0$), a fun o de la velocidade angular ($\omega$) em rela o a o tempo ($t$), juntamente com as vari veis adicionais la velocidade angular inicial ($\omega_0$) e o tempo inicial ($t_0$), expressa pela equa o:
A partir desta equa o, poss vel calcular a rela o entre o ângulo ($\theta$) e o ângulo inicial ($\theta_0$), bem como a mudan a na velocidade angular:
Se dividirmos a rela o entre la velocidade média ($\bar{v}$), o rádio ($r$) e la velocidade angular média ($\bar{\omega}$), expressa na seguinte equa o:
pelo valor de o tempo decorrido ($\Delta t$), podemos obter o fator que nos permite calcular a acelera o angular ao longo da rbita:
Se dividirmos a rela o entre la velocidade média ($\bar{v}$), o rádio ($r$) e la velocidade angular média ($\bar{\omega}$), expressa na seguinte equa o:
pelo valor de o tempo decorrido ($\Delta t$), podemos obter o fator que nos permite calcular a acelera o angular ao longo da rbita:
ID:(1409, 0)