Interceptar em aceleração angular constante
Storyboard 
Os objetos podem cruzar-se quando coincidem no ângulo no mesmo instante. Para isso, devem mover-se desde os seus respectivos ângulos e velocidades angulares iniciais com acelerações angulares que lhes permitam coincidir no ângulo e no tempo no final do percurso.
ID:(1451, 0)
Interceptar em aceleração angular constante
Storyboard 
Os objetos podem cruzar-se quando coincidem no ângulo no mesmo instante. Para isso, devem mover-se desde os seus respectivos ângulos e velocidades angulares iniciais com acelerações angulares que lhes permitam coincidir no ângulo e no tempo no final do percurso.
Variáveis
Cálculos
Cálculos
Equações
A defini o da acelera o angular m dia baseada no ngulo percorrido
e no tempo decorrido
A rela o entre os dois definida como a acelera o angular m dia
dentro desse intervalo de tempo.
A defini o da acelera o angular m dia baseada no ngulo percorrido
e no tempo decorrido
A rela o entre os dois definida como a acelera o angular m dia
dentro desse intervalo de tempo.
Dado que la aceleração média ($\bar{a}$) igual a la diferença de velocidade ($\Delta v$) e o tempo decorrido ($\Delta t$) conforme
e la aceleração angular média ($\bar{\alpha}$) igual a la diferença de velocidades angulares ($\Delta\omega$) e o tempo decorrido ($\Delta t$) conforme
deduz-se que
$\bar{a}=\displaystyle\frac{\Delta v}{\Delta t}=r\displaystyle\frac{\Delta\omega}{\Delta t}=\bar{\alpha}$
Assumindo que la aceleração angular média ($\bar{\alpha}$) igual a la aceleração angular constante ($\alpha_0$)
e supondo que la aceleração média ($\bar{a}$) igual a la aceleração constante ($a_0$)
obt m-se a seguinte equa o:
Dado que la aceleração média ($\bar{a}$) igual a la diferença de velocidade ($\Delta v$) e o tempo decorrido ($\Delta t$) conforme
e la aceleração angular média ($\bar{\alpha}$) igual a la diferença de velocidades angulares ($\Delta\omega$) e o tempo decorrido ($\Delta t$) conforme
deduz-se que
$\bar{a}=\displaystyle\frac{\Delta v}{\Delta t}=r\displaystyle\frac{\Delta\omega}{\Delta t}=\bar{\alpha}$
Assumindo que la aceleração angular média ($\bar{\alpha}$) igual a la aceleração angular constante ($\alpha_0$)
e supondo que la aceleração média ($\bar{a}$) igual a la aceleração constante ($a_0$)
obt m-se a seguinte equa o:
Se assumirmos que la aceleração angular média ($\bar{\alpha}$) constante, equivalente a la aceleração angular constante ($\alpha_0$), ent o a seguinte equa o se aplica:
Portanto, considerando la diferença de velocidades angulares ($\Delta\omega$) junto com la velocidade angular ($\omega$) e la velocidade angular inicial ($\omega_0$):
e o tempo decorrido ($\Delta t$) em rela o a o tempo ($t$) e o tempo inicial ($t_0$):
a equa o para la aceleração angular média ($\bar{\alpha}$):
pode ser expressa como:
$\alpha_0 = \alpha = \displaystyle\frac{\Delta \omega}{\Delta t} = \displaystyle\frac{\omega - \omega_0}{t - t_0}$
Resolvendo isso, obtemos:
Se assumirmos que la aceleração angular média ($\bar{\alpha}$) constante, equivalente a la aceleração angular constante ($\alpha_0$), ent o a seguinte equa o se aplica:
Portanto, considerando la diferença de velocidades angulares ($\Delta\omega$) junto com la velocidade angular ($\omega$) e la velocidade angular inicial ($\omega_0$):
e o tempo decorrido ($\Delta t$) em rela o a o tempo ($t$) e o tempo inicial ($t_0$):
a equa o para la aceleração angular média ($\bar{\alpha}$):
pode ser expressa como:
$\alpha_0 = \alpha = \displaystyle\frac{\Delta \omega}{\Delta t} = \displaystyle\frac{\omega - \omega_0}{t - t_0}$
Resolvendo isso, obtemos:
No caso de la aceleração angular constante ($\alpha_0$), la velocidade angular ($\omega$) como fun o de o tempo ($t$) segue uma rela o linear com o tempo inicial ($t_0$) e la velocidade angular inicial ($\omega_0$) na forma:
Dado que o deslocamento angular igual rea sob a curva de velocidade angular-tempo, neste caso, pode-se adicionar as contribui es do ret ngulo:
$\omega_0(t-t_0)$
e do tri ngulo:
$\displaystyle\frac{1}{2}\alpha_0(t-t_0)^2$
Isso nos leva express o para o ângulo ($\theta$) e o ângulo inicial ($\theta_0$):
No caso de la aceleração angular constante ($\alpha_0$), la velocidade angular ($\omega$) como fun o de o tempo ($t$) segue uma rela o linear com o tempo inicial ($t_0$) e la velocidade angular inicial ($\omega_0$) na forma:
Dado que o deslocamento angular igual rea sob a curva de velocidade angular-tempo, neste caso, pode-se adicionar as contribui es do ret ngulo:
$\omega_0(t-t_0)$
e do tri ngulo:
$\displaystyle\frac{1}{2}\alpha_0(t-t_0)^2$
Isso nos leva express o para o ângulo ($\theta$) e o ângulo inicial ($\theta_0$):
Se resolvermos o tempo na equa o de la velocidade angular ($\omega$) que inclui as vari veis la velocidade angular inicial ($\omega_0$), o tempo ($t$), o tempo inicial ($t_0$) e la aceleração angular constante ($\alpha_0$):
obtemos a seguinte express o para o tempo:
$t - t_0 = \displaystyle\frac{\omega - \omega_0}{\alpha_0}$
Esta solu o pode ser substitu da na equa o para calcular o ângulo ($\theta$) usando o ângulo inicial ($\theta_0$) da seguinte forma:
o que resulta na seguinte equa o:
Se resolvermos o tempo na equa o de la velocidade angular ($\omega$) que inclui as vari veis la velocidade angular inicial ($\omega_0$), o tempo ($t$), o tempo inicial ($t_0$) e la aceleração angular constante ($\alpha_0$):
obtemos a seguinte express o para o tempo:
$t - t_0 = \displaystyle\frac{\omega - \omega_0}{\alpha_0}$
Esta solu o pode ser substitu da na equa o para calcular o ângulo ($\theta$) usando o ângulo inicial ($\theta_0$) da seguinte forma:
o que resulta na seguinte equa o:
Exemplos
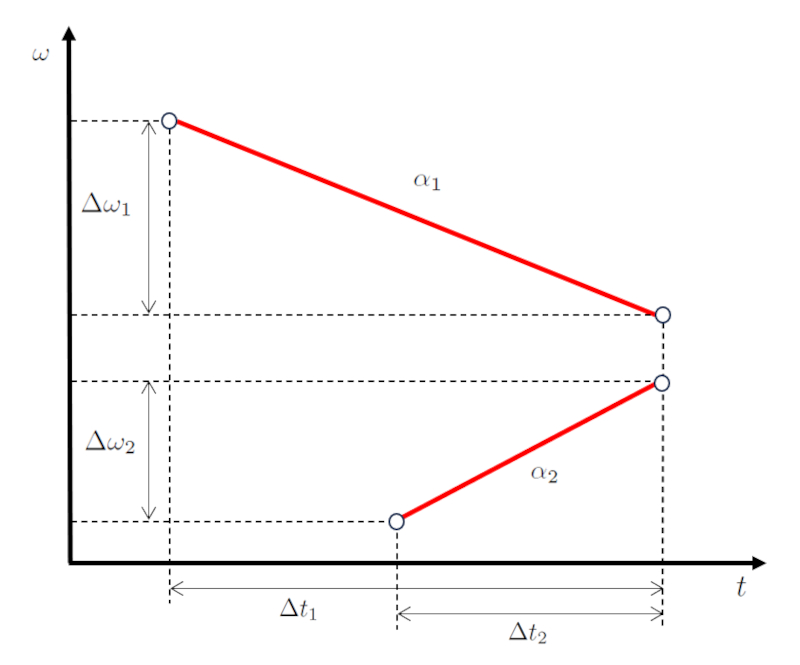
Em um cen rio de movimento de dois corpos, o primeiro altera la diferença de velocidade angular do primeiro corpo ($\Delta\omega_1$) durante la tempo de percurso do primeiro objeto ($\Delta t_1$) com la aceleração angular do primeiro corpo ($\alpha_1$).
Posteriormente, o segundo corpo avan a, alterando la diferença de velocidade angular do segundo corpo ($\Delta\omega_2$) durante la tempo de percurso do segundo objeto ($\Delta t_2$) com la aceleração angular do segundo corpo ($\alpha_2$).
Representado graficamente, obtemos um diagrama de velocidade e tempo como mostrado abaixo:
A chave aqui que os valores la diferença de velocidade angular do primeiro corpo ($\Delta\omega_1$) e la diferença de velocidade angular do segundo corpo ($\Delta\omega_2$), e os valores la tempo de percurso do primeiro objeto ($\Delta t_1$) e la tempo de percurso do segundo objeto ($\Delta t_2$), s o tais que ambos os corpos coincidem em ngulo e tempo.
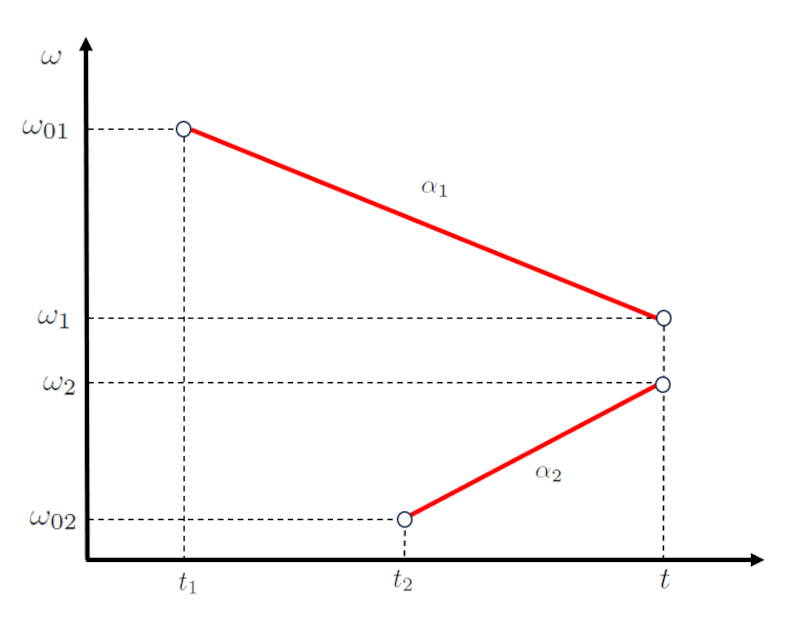
No caso de dois corpos, o movimento do primeiro pode ser descrito por uma fun o que envolve os pontos la velocidade angular inicial do primeiro corpo ($\omega_{01}$), la velocidade angular final do primeiro corpo ($\omega_1$), o tempo de interseção ($t$) e o tempo inicial do primeiro objeto ($t_1$), representada por uma reta com uma inclina o de la aceleração angular do primeiro corpo ($\alpha_1$):
Para o movimento do segundo corpo, definido pelos pontos la velocidade angular inicial do segundo corpo ($\omega_{02}$), la velocidade angular final do segundo corpo ($\omega_2$), o tempo inicial do segundo objeto ($t_2$) e o tempo de interseção ($t$), utiliza-se uma segunda reta com uma inclina o de la aceleração angular do segundo corpo ($\alpha_2$):
Isso representado como:
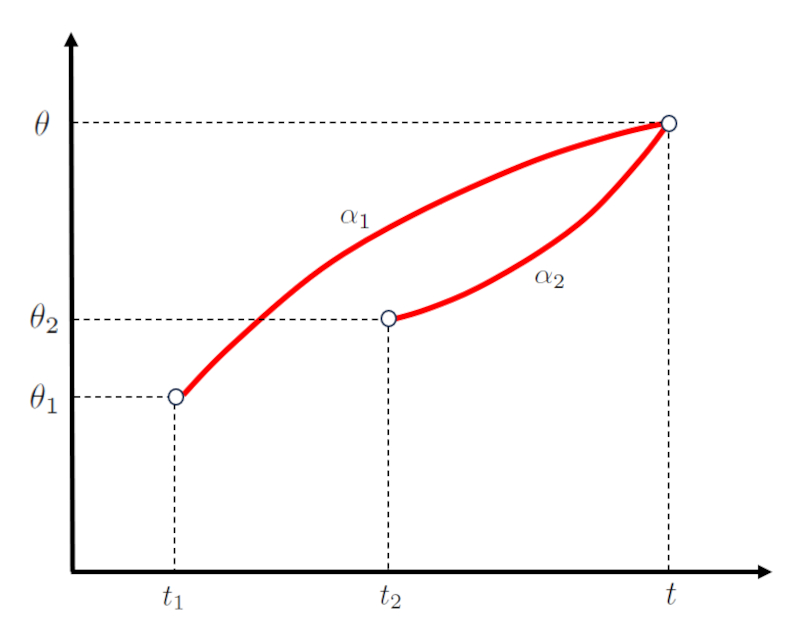
No caso de um movimento de dois corpos, o ngulo em que a trajet ria do primeiro termina coincide com o do segundo corpo em la ângulo de intersecção ($\theta$).
Da mesma forma, o tempo em que a trajet ria do primeiro termina coincide com a do segundo corpo em o tempo de interseção ($t$).
Para o primeiro corpo, la ângulo de intersecção ($\theta$) depende de o ângulo inicial do primeiro corpo ($\theta_1$), la velocidade angular inicial do primeiro corpo ($\omega_{01}$), la aceleração angular do primeiro corpo ($\alpha_1$), o tempo inicial do primeiro objeto ($t_1$), conforme:
Enquanto que para o segundo corpo, la ângulo de intersecção ($\theta$) depende de o ângulo inicial do segundo corpo ($\theta_2$), la velocidade angular inicial do segundo corpo ($\omega_{02}$), la aceleração angular do segundo corpo ($\alpha_2$), o tempo inicial do segundo objeto ($t_2$), conforme:
Isso representado como:
A acelera o definida como a varia o da velocidade angular por unidade de tempo.
Portanto, a acelera o angular la diferença de velocidades angulares ($\Delta\omega$) pode ser expressa em termos da velocidade angular la velocidade angular ($\omega$) e do tempo la velocidade angular inicial ($\omega_0$) da seguinte forma:
A acelera o definida como a varia o da velocidade angular por unidade de tempo.
Portanto, a acelera o angular la diferença de velocidades angulares ($\Delta\omega$) pode ser expressa em termos da velocidade angular la velocidade angular ($\omega$) e do tempo la velocidade angular inicial ($\omega_0$) da seguinte forma:
Para descrever o movimento de um objeto, precisamos calcular o tempo decorrido ($\Delta t$). Essa magnitude obtida medindo o tempo inicial ($t_0$) e o o tempo ($t$) desse movimento. A dura o determinada subtraindo o tempo inicial do tempo final:
Para descrever o movimento de um objeto, precisamos calcular o tempo decorrido ($\Delta t$). Essa magnitude obtida medindo o tempo inicial ($t_0$) e o o tempo ($t$) desse movimento. A dura o determinada subtraindo o tempo inicial do tempo final:
A taxa na qual a velocidade angular varia ao longo do tempo definida como la aceleração angular média ($\bar{\alpha}$). Para medi-la, necess rio observar la diferença de velocidades angulares ($\Delta\omega$) e o tempo decorrido ($\Delta t$).
A equa o que descreve la aceleração angular média ($\bar{\alpha}$) a seguinte:
A taxa na qual a velocidade angular varia ao longo do tempo definida como la aceleração angular média ($\bar{\alpha}$). Para medi-la, necess rio observar la diferença de velocidades angulares ($\Delta\omega$) e o tempo decorrido ($\Delta t$).
A equa o que descreve la aceleração angular média ($\bar{\alpha}$) a seguinte:
Com la aceleração angular constante ($\alpha_0$), la velocidade angular ($\omega$) forma uma rela o linear com o tempo ($t$), incorporando as vari veis la velocidade angular inicial ($\omega_0$) e o tempo inicial ($t_0$) da seguinte forma:
Esta equa o representa uma linha reta no plano de velocidade angular versus tempo.
Com la aceleração angular constante ($\alpha_0$), la velocidade angular ($\omega$) forma uma rela o linear com o tempo ($t$), incorporando as vari veis la velocidade angular inicial ($\omega_0$) e o tempo inicial ($t_0$) da seguinte forma:
Esta equa o representa uma linha reta no plano de velocidade angular versus tempo.
Dado que o deslocamento total corresponde rea sob a curva de velocidade angular versus tempo, no caso de uma aceleração angular constante ($\alpha_0$), determina-se que o deslocamento o ângulo ($\theta$) com as vari veis o ângulo inicial ($\theta_0$), o tempo ($t$), o tempo inicial ($t_0$) e la velocidade angular inicial ($\omega_0$) o seguinte:
Essa express o corresponde forma geral de uma par bola.
Dado que o deslocamento total corresponde rea sob a curva de velocidade angular versus tempo, no caso de uma aceleração angular constante ($\alpha_0$), determina-se que o deslocamento o ângulo ($\theta$) com as vari veis o ângulo inicial ($\theta_0$), o tempo ($t$), o tempo inicial ($t_0$) e la velocidade angular inicial ($\omega_0$) o seguinte:
Essa express o corresponde forma geral de uma par bola.
No caso de la aceleração angular constante ($\alpha_0$), a fun o de la velocidade angular ($\omega$) em rela o a o tempo ($t$), juntamente com as vari veis adicionais la velocidade angular inicial ($\omega_0$) e o tempo inicial ($t_0$), expressa pela equa o:
A partir desta equa o, poss vel calcular a rela o entre o ângulo ($\theta$) e o ângulo inicial ($\theta_0$), bem como a mudan a na velocidade angular:
No caso de la aceleração angular constante ($\alpha_0$), a fun o de la velocidade angular ($\omega$) em rela o a o tempo ($t$), juntamente com as vari veis adicionais la velocidade angular inicial ($\omega_0$) e o tempo inicial ($t_0$), expressa pela equa o:
A partir desta equa o, poss vel calcular a rela o entre o ângulo ($\theta$) e o ângulo inicial ($\theta_0$), bem como a mudan a na velocidade angular:
Para descrever a rota o de um objeto, precisamos determinar la variação de ângulo ($\Delta\theta$). Isso feito subtraindo o ângulo inicial ($\theta_0$) do valor alcan ado pelo objeto durante sua rota o, que o ângulo ($\theta$):
Para descrever a rota o de um objeto, precisamos determinar la variação de ângulo ($\Delta\theta$). Isso feito subtraindo o ângulo inicial ($\theta_0$) do valor alcan ado pelo objeto durante sua rota o, que o ângulo ($\theta$):
Se dividirmos a rela o entre la velocidade média ($\bar{v}$), o rádio ($r$) e la velocidade angular média ($\bar{\omega}$), expressa na seguinte equa o:
pelo valor de o tempo decorrido ($\Delta t$), podemos obter o fator que nos permite calcular a acelera o angular ao longo da rbita:
Se dividirmos a rela o entre la velocidade média ($\bar{v}$), o rádio ($r$) e la velocidade angular média ($\bar{\omega}$), expressa na seguinte equa o:
pelo valor de o tempo decorrido ($\Delta t$), podemos obter o fator que nos permite calcular a acelera o angular ao longo da rbita:
ID:(1451, 0)