Accélération angulaire constante, deux étapes
Storyboard 
Dans le cas d'un mouvement angulaire accéléré en deux étapes, au moment où l'on passe de la première à la deuxième accélération angulaire, la vitesse angulaire finale de la première étape devient la vitesse angulaire initiale de la deuxième. Il en va de même pour l'angle, où l'angle final de la première étape est égal à l'angle initial de la deuxième étape.
Contrairement au modèle à deux vitesses angulaires, ce modèle ne présente pas de problèmes de discontinuité, sauf si l'accélération angulaire peut changer de manière abrupte, ce qui est techniquement possible mais souvent peu réaliste.
ID:(1409, 0)
Accélération angulaire constante, deux étapes
Storyboard 
Dans le cas d'un mouvement angulaire accéléré en deux étapes, au moment où l'on passe de la première à la deuxième accélération angulaire, la vitesse angulaire finale de la première étape devient la vitesse angulaire initiale de la deuxième. Il en va de même pour l'angle, où l'angle final de la première étape est égal à l'angle initial de la deuxième étape. Contrairement au modèle à deux vitesses angulaires, ce modèle ne présente pas de problèmes de discontinuité, sauf si l'accélération angulaire peut changer de manière abrupte, ce qui est techniquement possible mais souvent peu réaliste.
Variables
Calculs
Calculs
Équations
La d finition de l'acc l ration angulaire moyenne repose sur l'angle parcouru
et le temps coul
La relation entre les deux est d finie comme l'acc l ration angulaire moyenne
pendant cet intervalle de temps.
La d finition de l'acc l ration angulaire moyenne repose sur l'angle parcouru
et le temps coul
La relation entre les deux est d finie comme l'acc l ration angulaire moyenne
pendant cet intervalle de temps.
tant donn que a accélération moyenne ($\bar{a}$) est gal a différence de vitesse ($\Delta v$) et le temps écoulé ($\Delta t$) selon
et que a accélération angulaire moyenne ($\bar{\alpha}$) est gal a différence de vitesses angulaires ($\Delta\omega$) et le temps écoulé ($\Delta t$) conform ment
il en d coule que
$\bar{a}=\displaystyle\frac{\Delta v}{\Delta t}=r\displaystyle\frac{\Delta\omega}{\Delta t}=\bar{\alpha}$
En supposant que a accélération angulaire moyenne ($\bar{\alpha}$) est gal a accélération angulaire constante ($\alpha_0$)
et en supposant que a accélération moyenne ($\bar{a}$) est gal a accélération constante ($a_0$)
on obtient l' quation suivante :
tant donn que a accélération moyenne ($\bar{a}$) est gal a différence de vitesse ($\Delta v$) et le temps écoulé ($\Delta t$) selon
et que a accélération angulaire moyenne ($\bar{\alpha}$) est gal a différence de vitesses angulaires ($\Delta\omega$) et le temps écoulé ($\Delta t$) conform ment
il en d coule que
$\bar{a}=\displaystyle\frac{\Delta v}{\Delta t}=r\displaystyle\frac{\Delta\omega}{\Delta t}=\bar{\alpha}$
En supposant que a accélération angulaire moyenne ($\bar{\alpha}$) est gal a accélération angulaire constante ($\alpha_0$)
et en supposant que a accélération moyenne ($\bar{a}$) est gal a accélération constante ($a_0$)
on obtient l' quation suivante :
Si nous supposons que a accélération angulaire moyenne ($\bar{\alpha}$) est constant, quivalent a accélération angulaire constante ($\alpha_0$), alors l' quation suivante s'applique :
Par cons quent, en consid rant a différence de vitesses angulaires ($\Delta\omega$) avec a vitesse angulaire ($\omega$) et a vitesse angulaire initiale ($\omega_0$) :
et le temps écoulé ($\Delta t$) en relation avec le temps ($t$) et le temps initial ($t_0$) :
l' quation pour a accélération angulaire moyenne ($\bar{\alpha}$) :
peut tre exprim e comme suit :
$\alpha_0 = \alpha = \displaystyle\frac{\Delta \omega}{\Delta t} = \displaystyle\frac{\omega - \omega_0}{t - t_0}$
En r solvant cela, nous obtenons :
Si nous supposons que a accélération angulaire moyenne ($\bar{\alpha}$) est constant, quivalent a accélération angulaire constante ($\alpha_0$), alors l' quation suivante s'applique :
Par cons quent, en consid rant a différence de vitesses angulaires ($\Delta\omega$) avec a vitesse angulaire ($\omega$) et a vitesse angulaire initiale ($\omega_0$) :
et le temps écoulé ($\Delta t$) en relation avec le temps ($t$) et le temps initial ($t_0$) :
l' quation pour a accélération angulaire moyenne ($\bar{\alpha}$) :
peut tre exprim e comme suit :
$\alpha_0 = \alpha = \displaystyle\frac{\Delta \omega}{\Delta t} = \displaystyle\frac{\omega - \omega_0}{t - t_0}$
En r solvant cela, nous obtenons :
Dans le cas de a accélération angulaire constante ($\alpha_0$), a vitesse angulaire ($\omega$) en fonction de le temps ($t$) suit une relation lin aire avec le temps initial ($t_0$) et a vitesse angulaire initiale ($\omega_0$) sous la forme :
tant donn que le d placement angulaire est gal l'aire sous la courbe de vitesse angulaire-temps, dans ce cas, on peut ajouter les contributions du rectangle :
$\omega_0(t-t_0)$
et du triangle :
$\displaystyle\frac{1}{2}\alpha_0(t-t_0)^2$
Cela nous m ne l'expression pour le angle ($\theta$) et le angle de départ ($\theta_0$) :
Dans le cas de a accélération angulaire constante ($\alpha_0$), a vitesse angulaire ($\omega$) en fonction de le temps ($t$) suit une relation lin aire avec le temps initial ($t_0$) et a vitesse angulaire initiale ($\omega_0$) sous la forme :
tant donn que le d placement angulaire est gal l'aire sous la courbe de vitesse angulaire-temps, dans ce cas, on peut ajouter les contributions du rectangle :
$\omega_0(t-t_0)$
et du triangle :
$\displaystyle\frac{1}{2}\alpha_0(t-t_0)^2$
Cela nous m ne l'expression pour le angle ($\theta$) et le angle de départ ($\theta_0$) :
Si nous r solvons le temps dans l' quation de a vitesse angulaire ($\omega$) qui inclut les variables a vitesse angulaire initiale ($\omega_0$), le temps ($t$), le temps initial ($t_0$) et a accélération angulaire constante ($\alpha_0$) :
nous obtenons l'expression suivante pour le temps :
$t - t_0 = \displaystyle\frac{\omega - \omega_0}{\alpha_0}$
Cette solution peut tre substitu e dans l' quation pour calculer le angle ($\theta$) en utilisant le angle de départ ($\theta_0$) de la mani re suivante :
ce qui donne la formule suivante :
Si nous r solvons le temps dans l' quation de a vitesse angulaire ($\omega$) qui inclut les variables a vitesse angulaire initiale ($\omega_0$), le temps ($t$), le temps initial ($t_0$) et a accélération angulaire constante ($\alpha_0$) :
nous obtenons l'expression suivante pour le temps :
$t - t_0 = \displaystyle\frac{\omega - \omega_0}{\alpha_0}$
Cette solution peut tre substitu e dans l' quation pour calculer le angle ($\theta$) en utilisant le angle de départ ($\theta_0$) de la mani re suivante :
ce qui donne la formule suivante :
Exemples
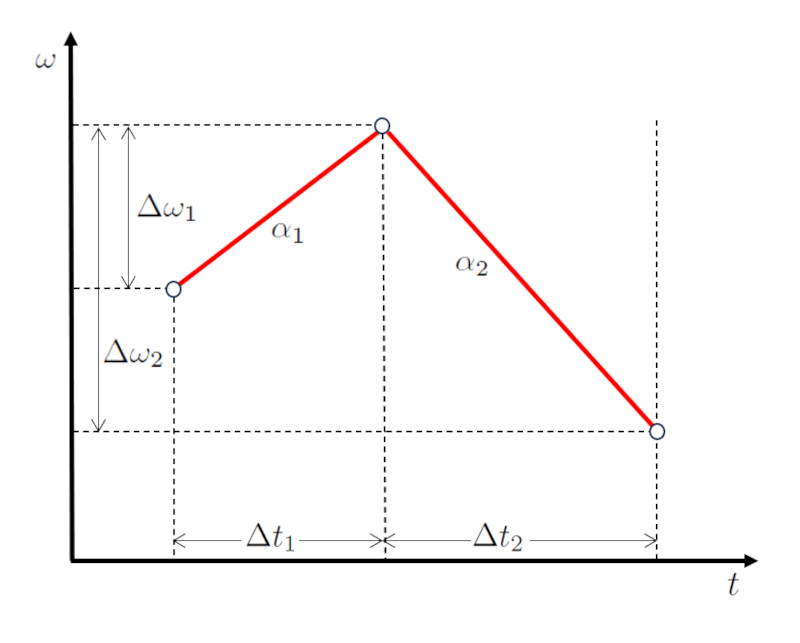
Dans un sc nario de mouvement en deux tapes, initialement l'objet ajuste sa vitesse de la diff rence de a variation des vitesses angulaires dans la première étape ($\Delta\omega_1$) sur une p riode de le temps écoulé dans la première étape ($\Delta t_1$), subissant une acc l ration de a accélération angulaire lors de la première étape ($\alpha_1$).
Dans la seconde tape, l'objet continue de modifier sa vitesse de a variation des vitesses angulaires dans la deuxième étape ($\Delta\omega_2$) sur une dur e de le temps passé dans la deuxième étape ($\Delta t_2$), avec une acc l ration de a accélération angulaire lors de la deuxième étape ($\alpha_2$).
Lorsqu'on repr sente cela graphiquement, on obtient un diagramme de vitesse contre temps comme montr ci-dessous :
Il est important de noter que les intervalles de temps le temps écoulé dans la première étape ($\Delta t_1$) et le temps passé dans la deuxième étape ($\Delta t_2$) sont cons cutifs, tout comme les diff rences de vitesse a variation des vitesses angulaires dans la première étape ($\Delta\omega_1$) et a variation des vitesses angulaires dans la deuxième étape ($\Delta\omega_2$).
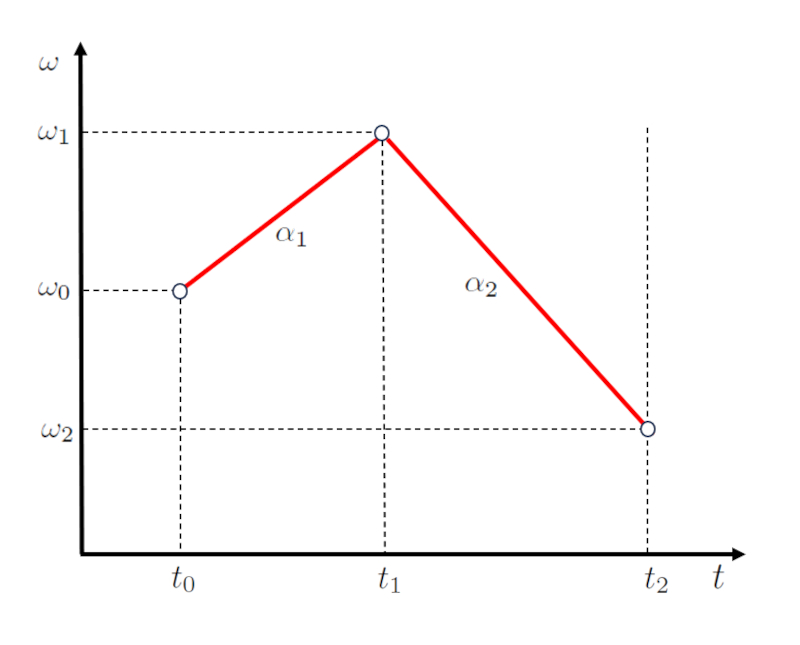
Dans l'analyse d'un mouvement segment en deux tapes, la premi re phase est caract ris e par une fonction lin aire qui int gre les points le temps initial ($t_0$), le temps final de la première et départ de la deuxième étape ($t_1$), a vitesse angulaire initiale ($\omega_0$) et a première vitesse angulaire finale et démarrage du deuxième étage ($\omega_1$). Celle-ci est exprim e par une droite dont la pente est a accélération angulaire lors de la première étape ($\alpha_1$), dont la relation math matique est sp cifi e dans l' quation suivante :
Lors de la transition vers la seconde tape, d finie par les points a première vitesse angulaire finale et démarrage du deuxième étage ($\omega_1$), a vitesse angulaire finale du deuxième étage ($\omega_2$), le temps final de la première et départ de la deuxième étape ($t_1$) et le heure de fin de la deuxième étape ($t_2$), une nouvelle fonction lin aire avec une pente de a accélération angulaire lors de la deuxième étape ($\alpha_2$) est adopt e. Cette relation est d taill e par la seconde quation pr sent e :
La repr sentation graphique de ces relations lin aires est illustr e ci-dessous, offrant une visualisation claire de la variation de la pente entre les deux tapes :
Dans un sc nario de mouvement divis en deux tapes, l'angle la fin de la premi re tape correspond l'angle au d but de la deuxi me tape, d sign par le début du premier angle final et de la deuxième étape ($\theta_1$).
De m me, le moment o se termine la premi re tape co ncide avec le d but de la deuxi me tape, marqu par le temps final de la première et départ de la deuxième étape ($t_1$).
tant donn que le mouvement est d fini par l'acc l ration angulaire subie, la vitesse angulaire la fin de la premi re tape doit correspondre la vitesse angulaire initiale de la deuxi me tape, indiqu e par a première vitesse angulaire finale et démarrage du deuxième étage ($\omega_1$).
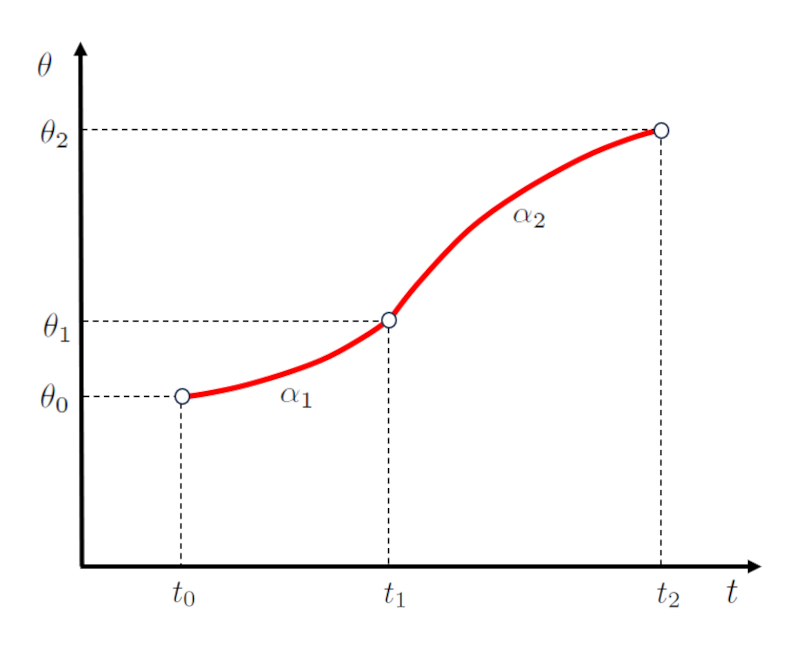
Dans le contexte d'une acc l ration angulaire constante, l'angle le début du premier angle final et de la deuxième étape ($\theta_1$) est d termin par les variables le angle de départ ($\theta_0$), a vitesse angulaire initiale ($\omega_0$), a accélération angulaire lors de la première étape ($\alpha_1$), le temps final de la première et départ de la deuxième étape ($t_1$) et le temps initial ($t_0$), comme indiqu dans l' quation suivante :
Dans la deuxi me tape, l'angle a angle final de la deuxième étape ($\theta_2$) est calcul sur la base de le début du premier angle final et de la deuxième étape ($\theta_1$), a première vitesse angulaire finale et démarrage du deuxième étage ($\omega_1$), a accélération angulaire lors de la deuxième étape ($\alpha_2$), le temps final de la première et départ de la deuxième étape ($t_1$) et le heure de fin de la deuxième étape ($t_2$), selon :
La repr sentation graphique de ces relations est illustr e ci-dessous :
Le taux auquel la vitesse angulaire varie dans le temps est d fini comme a accélération angulaire moyenne ($\bar{\alpha}$). Pour le mesurer, il est n cessaire d'observer a différence de vitesses angulaires ($\Delta\omega$) et le temps écoulé ($\Delta t$).
L' quation qui d crit a accélération angulaire moyenne ($\bar{\alpha}$) est la suivante :
Le taux auquel la vitesse angulaire varie dans le temps est d fini comme a accélération angulaire moyenne ($\bar{\alpha}$). Pour le mesurer, il est n cessaire d'observer a différence de vitesses angulaires ($\Delta\omega$) et le temps écoulé ($\Delta t$).
L' quation qui d crit a accélération angulaire moyenne ($\bar{\alpha}$) est la suivante :
Pour d crire la rotation d'un objet, nous devons d terminer a variation d'angle ($\Delta\theta$). Cela se fait en soustrayant le angle de départ ($\theta_0$) de le angle ($\theta$), la valeur atteinte par l'objet pendant sa rotation:
Pour d crire la rotation d'un objet, nous devons d terminer a variation d'angle ($\Delta\theta$). Cela se fait en soustrayant le angle de départ ($\theta_0$) de le angle ($\theta$), la valeur atteinte par l'objet pendant sa rotation:
L'acc l ration est d finie comme le changement de vitesse angulaire par unit de temps.
Par cons quent, l'acc l ration angulaire a différence de vitesses angulaires ($\Delta\omega$) peut tre exprim e en termes de vitesse angulaire a vitesse angulaire ($\omega$) et de temps a vitesse angulaire initiale ($\omega_0$) comme suit :
L'acc l ration est d finie comme le changement de vitesse angulaire par unit de temps.
Par cons quent, l'acc l ration angulaire a différence de vitesses angulaires ($\Delta\omega$) peut tre exprim e en termes de vitesse angulaire a vitesse angulaire ($\omega$) et de temps a vitesse angulaire initiale ($\omega_0$) comme suit :
Pour d crire le mouvement d'un objet, nous devons calculer le temps écoulé ($\Delta t$). Cette grandeur est obtenue en mesurant le temps initial ($t_0$) et le le temps ($t$) de ce mouvement. La dur e est d termin e en soustrayant le temps initial du temps final :
Pour d crire le mouvement d'un objet, nous devons calculer le temps écoulé ($\Delta t$). Cette grandeur est obtenue en mesurant le temps initial ($t_0$) et le le temps ($t$) de ce mouvement. La dur e est d termin e en soustrayant le temps initial du temps final :
Avec a accélération angulaire constante ($\alpha_0$), a vitesse angulaire ($\omega$) tablit une relation lin aire avec le temps ($t$), int grant galement les variables a vitesse angulaire initiale ($\omega_0$) et le temps initial ($t_0$) comme suit :
Cette quation repr sente une droite dans le plan de la vitesse angulaire par rapport au temps.
Avec a accélération angulaire constante ($\alpha_0$), a vitesse angulaire ($\omega$) tablit une relation lin aire avec le temps ($t$), int grant galement les variables a vitesse angulaire initiale ($\omega_0$) et le temps initial ($t_0$) comme suit :
Cette quation repr sente une droite dans le plan de la vitesse angulaire par rapport au temps.
tant donn que le d placement total correspond l'aire sous la courbe de vitesse angulaire par rapport au temps, dans le cas de une accélération angulaire constante ($\alpha_0$), il est d termin que le d placement le angle ($\theta$) avec les variables le angle de départ ($\theta_0$), le temps ($t$), le temps initial ($t_0$) et a vitesse angulaire initiale ($\omega_0$) est le suivant :
Cette expression correspond la forme g n rale d\'une parabole.
tant donn que le d placement total correspond l'aire sous la courbe de vitesse angulaire par rapport au temps, dans le cas de une accélération angulaire constante ($\alpha_0$), il est d termin que le d placement le angle ($\theta$) avec les variables le angle de départ ($\theta_0$), le temps ($t$), le temps initial ($t_0$) et a vitesse angulaire initiale ($\omega_0$) est le suivant :
Cette expression correspond la forme g n rale d\'une parabole.
Dans le cas de a accélération angulaire constante ($\alpha_0$), la fonction de a vitesse angulaire ($\omega$) par rapport le temps ($t$), avec les variables suppl mentaires a vitesse angulaire initiale ($\omega_0$) et le temps initial ($t_0$), est exprim e par l' quation :
partir de cette quation, il est possible de calculer la relation entre le angle ($\theta$) et le angle de départ ($\theta_0$), ainsi que le changement de vitesse angulaire :
Dans le cas de a accélération angulaire constante ($\alpha_0$), la fonction de a vitesse angulaire ($\omega$) par rapport le temps ($t$), avec les variables suppl mentaires a vitesse angulaire initiale ($\omega_0$) et le temps initial ($t_0$), est exprim e par l' quation :
partir de cette quation, il est possible de calculer la relation entre le angle ($\theta$) et le angle de départ ($\theta_0$), ainsi que le changement de vitesse angulaire :
Si nous divisons la relation entre a vitesse moyenne ($\bar{v}$), le radio ($r$) et a vitesse angulaire moyenne ($\bar{\omega}$), exprim e dans l' quation suivante :
par la valeur de le temps écoulé ($\Delta t$), nous pouvons obtenir le facteur qui nous permet de calculer l'acc l ration angulaire le long de l'orbite :
Si nous divisons la relation entre a vitesse moyenne ($\bar{v}$), le radio ($r$) et a vitesse angulaire moyenne ($\bar{\omega}$), exprim e dans l' quation suivante :
par la valeur de le temps écoulé ($\Delta t$), nous pouvons obtenir le facteur qui nous permet de calculer l'acc l ration angulaire le long de l'orbite :
ID:(1409, 0)