Usuario:
Ley General de los Gases Ideales
Storyboard
Las tres leyes de los gases (ley de Boyle-Mariotte, ley de Charles, ley de Gay-Laussac) y el principio de Avogadro pueden ser combinadas en una sola ley que se denomina la ley de los gases ideales.
Esto permite predecir para un gas ideal la variación de uno de los parámetros que definen el estado del gas (presión $p$, volumen $V$, temperatura absoluta $T$ y numero de moles $n$) en base a el estado inicial y cualquier estado final definido por las restantes tres variables.
ID:(1476, 0)
Leyes de los Gases
Concepto
El estado de un sistema se describe mediante la llamada ecuación de estado, que establece la relación entre los parámetros que caracterizan dicho sistema.
En el caso de los gases, los parámetros que describen su estado son la presión ($p$), el volumen ($V$), la temperatura absoluta ($T$) y el número de moles ($n$). Generalmente, este último parámetro se mantiene constante, ya que está relacionado con la cantidad de gas presente.
La ecuación de estado relaciona, por lo tanto, la presión, el volumen y la temperatura, y establece que existen solo dos grados de libertad, ya que la ecuación de estado permite calcular el tercer parámetro. En particular, si se fija el volumen, se puede elegir, por ejemplo, la temperatura como variable, lo que permite calcular la presión correspondiente.
ID:(587, 0)
Integrando las leyes de los gases
Descripción
Las tres leyes de los gases que relacionan la presión ($p$), el volumen ($V$) y la temperatura absoluta ($T$) son:
• La ley de Boyle, que establece que a temperatura constante, el producto de la presión y el volumen de un gas es constante:
| $ p V = C_{pV} $ |
• La ley de Charles, que establece que a presión constante, el volumen de un gas es directamente proporcional a su temperatura absoluta:
| $\displaystyle\frac{ V }{ T } = C_{VT}$ |
• La ley de Gay-Lussac, que establece que a volumen constante, la presión de un gas es directamente proporcional a su temperatura absoluta:
| $\displaystyle\frac{ p }{ T } = C_{pT}$ |
Estas leyes se pueden representar gráficamente como se muestra en la siguiente imagen:
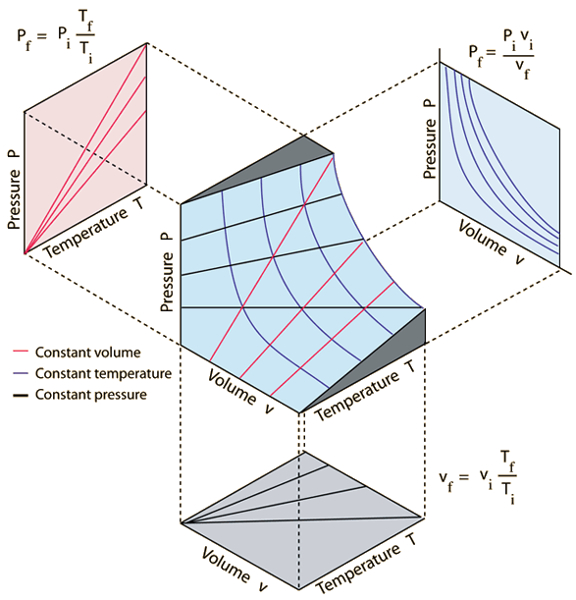
Diagram presión, volumen, temperatura de un gas ideal (http://hyperphysics.phy-astr.gsu.edu)
ID:(9525, 0)
Ley General de los Gases
Ecuación
En 1834, Émile Clapeyron reconoció que la presión ($p$), el volumen ($V$), la temperatura absoluta ($T$) y el número de moles ($n$) se relacionan mediante la ley de Boyle, la ley de Charles, la ley de Gay-Lussac y la ley de Avogadro. Estas leyes se pueden reescribir en la forma:
 $ p V = n R T $ |
La presión ($p$), el volumen ($V$), la temperatura absoluta ($T$) y el número de moles ($n$) están vinculados a través de las siguientes leyes físicas:
• La ley de Boyle
| $ p V = C_{pV} $ |
• La ley de Charles
| $\displaystyle\frac{ V }{ T } = C_{VT}$ |
• La ley de Gay-Lussac
| $\displaystyle\frac{ p }{ T } = C_{pT}$ |
• La ley de Avogadro
| $\displaystyle\frac{ n }{ V } = C_{nV} $ |
Estas leyes pueden ser expresadas de manera más general como:
$\displaystyle\frac{pV}{nT}=cte$
Esta relación general establece que el producto de la presión y el volumen dividido por el número de moles y la temperatura se mantiene constante:
| $ p V = n R T $ |
En esta ecuación, la constante universal de los gases ($R$) asume el valor 8.314 J/K·mol.
ID:(3183, 0)
Cambio de estado de un gas Ideal según ley general de los gases
Ecuación
Existe otra manera de expresar la ecuación de los gases al considerar la relación entre la presión ($p$), el volumen ($V$), la temperatura absoluta ($T$) y el número de moles ($n$) con la constante universal de los gases ($R$) es
| $ p V = n R T $ |
Como la constante universal de los gases ($R$) es una constante se puede despejar en ella e igualar la situación para un estado inicial (la presión en estado inicial ($p_i$), el volumen en estado i ($V_i$), la temperatura en estado inicial ($T_i$) y el número de moles en estado i ($n_i$)) y un estado final (la presión en estado final ($p_f$), el volumen en estado f ($V_f$), la temperatura en estado final ($T_f$) y el número de moles en estado f ($n_f$)):
| $\displaystyle\frac{ p_i V_i }{ n_i T_i }=\displaystyle\frac{ p_f V_f }{ n_f T_f }$ |
La ley de los gases ideales es
| $ p V = n R T $ |
se puede expresar como
$\displaystyle\frac{pV}{nT} = R$
Esto implica que las condiciones iniciales y finales deben cumplir con la igualdad
$\displaystyle\frac{p_iV_i}{n_iT_i} = R = \displaystyle\frac{p_fV_f}{n_fT_f}$
Así obtenemos la siguiente ecuación:
| $\displaystyle\frac{ p_i V_i }{ n_i T_i }=\displaystyle\frac{ p_f V_f }{ n_f T_f }$ |
ID:(9526, 0)
Presión en función de la concentración molar
Ecuación
Cuando la presión ($p$) se comporta como un gas ideal y cumple con el volumen ($V$), el número de moles ($n$), la temperatura absoluta ($T$), y la constante universal de los gases ($R$), la ecuación de los gases:
| $ p V = n R T $ |
puede ser reformulada en términos de la concentración molar ($c_m$) como:
| $ p = c_m R T $ |
Cuando la presión ($p$) se comporta como un gas ideal, cumpliendo con el volumen ($V$), el número de moles ($n$), la temperatura absoluta ($T$) y la constante universal de los gases ($R$), la ecuación de los gases:
| $ p V = n R T $ |
y la definición de la concentración molar ($c_m$):
| $ c_m \equiv\displaystyle\frac{ n }{ V }$ |
llevan a la siguiente relación:
| $ p = c_m R T $ |
ID:(4479, 0)
Presión en función de la densidad
Ecuación
La ecuación de los gases se puede reformular sustituyendo el número de moles ($n$) por su relación con la densidad ($\rho$). De esta manera, obtenemos la siguiente expresión en la que la presión ($p$) se relaciona con la temperatura absoluta ($T$), la masa molar ($M_m$) y la constante universal de los gases ($R$):
| $ p = \displaystyle\frac{ \rho }{ M_m } R T $ |
La presión ($p$) se puede expresar en términos de la concentración molar ($c_m$), la temperatura absoluta ($T$) y la constante universal de los gases ($R$) mediante la ecuación:
| $ p = c_m R T $ |
Y ya que la concentración molar ($c_m$) es igual a la densidad ($\rho$) y la masa molar ($M_m$):
| $ c_m =\displaystyle\frac{ \rho }{ M_m }$ |
Obtenemos la siguiente expresión:
| $ p = \displaystyle\frac{ \rho }{ M_m } R T $ |
ID:(8831, 0)
Constante específica de los gases
Ecuación
Si trabajamos con densidad en lugar de concentración molar, la ecuación para los gases con la presión ($p$), la densidad ($\rho$), la temperatura absoluta ($T$), la masa molar ($M_m$) y la constante universal de los gases ($R$) se puede expresar como:
| $ p = \displaystyle\frac{ \rho }{ M_m } R T $ |
En esta ecuación, podemos definir una constante específica análoga a la constante universal de los gases ($R$). Esto se logra introduciendo la constante específica de los gases ($R_s$) de la siguiente manera:
| $ R_s =\displaystyle\frac{ R }{ M_m }$ |
ID:(8832, 0)
Ley específica de los gases
Ecuación
Si trabajamos con la masa o la densidad ($\rho$) del gas, podemos establecer una ecuación análoga a la de los gases ideales para la presión ($p$) y la temperatura absoluta ($T$), con la única diferencia de que la constante será específica para cada tipo de gas y se denotará como la constante específica de los gases ($R_s$):
| $ p = \rho R_s T $ |
Si introducimos la ecuación de los gases escrita con la presión ($p$), la densidad ($\rho$), la constante universal de los gases ($R$), la temperatura absoluta ($T$) y la masa molar ($M_m$) como
| $ p = \displaystyle\frac{ \rho }{ M_m } R T $ |
y utilizamos la definición la constante específica de los gases ($R_s$) dada por
| $ R_s =\displaystyle\frac{ R }{ M_m }$ |
podemos derivar una ecuación específica para los gases de la siguiente manera:
| $ p = \rho R_s T $ |
ID:(8833, 0)
Video: Ley General de los Gases Ideales
Video
Mini clase que explica los conceptos y el desarrollo de las ecuaciones claves del tema.
ID:(11210, 0)
Video: Numero de Moles
Video
Mini clase que explica los conceptos y el desarrollo de las ecuaciones claves del tema.
ID:(11211, 0)