General Law of Ideal Gases
Storyboard 
The three gas laws (Boyle's Law, Charles's Law, Gay-Lussac's Law) and Avogadro's principle can be combined into a single law called the ideal gas law.
This allows predicting the variation of one of the parameters that define the state of the gas (the pressure ($p$), the volume ($V$), the absolute temperature ($T$), and the number of moles ($n$)) for an ideal gas, based on the initial state and any final state defined by the remaining three variables.
ID:(1476, 0)
Mechanisms
Definition 
The universal gas law, also known as the ideal gas law, describes the relationship between the pressure, volume, temperature, and number of moles of a gas. It combines several gas laws, including Boyle's law, Charles's law, and Avogadro's principle, into a single equation. This law states that the product of the pressure and volume of a gas is directly proportional to the product of its temperature and the number of moles of gas. The ideal gas law assumes that gases are composed of a large number of molecules that are in constant, random motion and that the interactions between these molecules are negligible. This law is fundamental in predicting the behavior of gases under various conditions and is widely used in both scientific research and practical applications, such as engineering and chemistry.
ID:(15258, 0)
Gas Laws
Image 
The state of a system is described by the so-called equation of state, which establishes the relationship between the parameters that characterize the system.
In the case of gases, the parameters that describe their state are the pressure ($p$), the volume ($V$), the absolute temperature ($T$), and the number of moles ($n$). Typically, the latter parameter remains constant as it is associated with the amount of gas present.
The equation of state, therefore, relates pressure, volume, and temperature, and it establishes that there are only two degrees of freedom, as the equation of state allows for the calculation of the third parameter. In particular, if the volume is fixed, one can choose, for example, temperature as the variable, which enables the calculation of the corresponding pressure.
ID:(587, 0)
Integrating the gas laws
Note 
The three gas laws that relate to the pressure ($p$), the volume ($V$), and the absolute temperature ($T$) are:
• Boyle's Law, which states that at constant temperature, the product of the pressure and the volume of a gas is constant:
| $ p V = C_b $ |
• Charles's Law, which states that at constant pressure, the volume of a gas is directly proportional to its absolute temperature:
| $\displaystyle\frac{ V }{ T } = C_c$ |
• Gay-Lussac's Law, which states that at constant volume, the pressure of a gas is directly proportional to its absolute temperature:
| $\displaystyle\frac{ p }{ T } = C_g$ |
These laws can be graphically represented as shown in the following image:
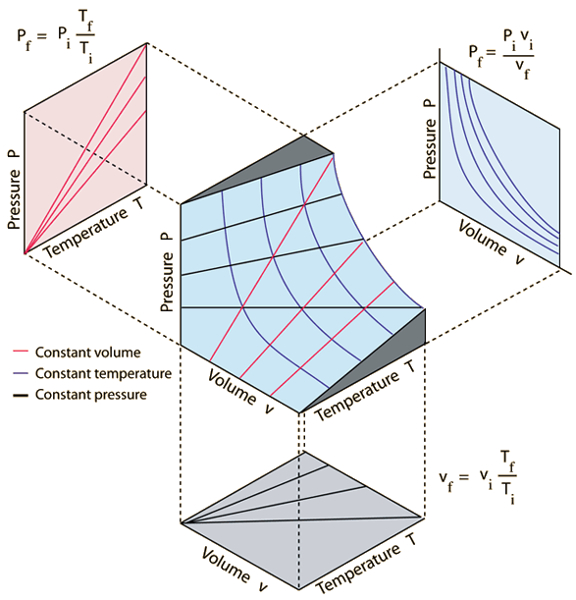
In 1834, Émile Clapeyron [1] recognized that the pressure ($p$), the volume ($V$), the absolute temperature ($T$), and the number of moles ($n$) are related by Boyle's law, Charles's law, Gay-Lussac's law, and Avogadro's law. These laws can be expressed more generally as:
$\displaystyle\frac{pV}{nT} = \text{constant}$
This general relationship states that the product of pressure and volume divided by the number of moles and the temperature remains constant:
| $ p V = n R_C T $ |
In this equation, the universal gas constant ($R_C$) assumes the value of 8.314 J/K·mol.
[1] "Mémoire sur la puissance motrice de la chaleur" (Memoir on the Motive Power of Heat), Émile Clapeyron, Journal de l'École Polytechnique, 1834.
ID:(9525, 0)
Change of state of an ideal gas according to the general gas law
Quote 
The ideal gas law is expressed as
| $ p V = n R_C T $ |
and can be written as
$\displaystyle\frac{pV}{nT} = R$
This implies that the initial and final conditions must satisfy the equality
$\displaystyle\frac{p_iV_i}{n_iT_i} = R = \displaystyle\frac{p_fV_f}{n_fT_f}$
Thus, we obtain the following equation:
| $\displaystyle\frac{ p_i V_i }{ n_i T_i }=\displaystyle\frac{ p_f V_f }{ n_f T_f }$ |
ID:(15683, 0)
Pressure as a function of molar concentration
Exercise 
When the pressure ($p$) behaves as an ideal gas, satisfying the volume ($V$), the number of moles ($n$), the absolute temperature ($T$), and the universal gas constant ($R_C$), the ideal gas equation:
| $ p V = n R_C T $ |
and the definition of the molar concentration ($c_m$):
| $ c_m \equiv\displaystyle\frac{ n }{ V }$ |
lead to the following relationship:
| $ p = c_m R_C T $ |
ID:(15684, 0)
Specific gas law
Equation 
The pressure ($p$) is associated with the volume ($V$), ERROR:6679, the absolute temperature ($T$), and the universal gas constant ($R_C$) through the equation:
| $ p V = n R_C T $ |
Since ERROR:6679 can be calculated with the mass ($M$) and the molar Mass ($M_m$) using:
| $ n = \displaystyle\frac{ M }{ M_m }$ |
and obtained with the definition of the specific gas constant ($R_s$) using:
| $ R_s \equiv \displaystyle\frac{ R_C }{ M_m }$ |
we conclude that:
| $ p V = M R_s T $ |
ID:(15685, 0)
Pressure as a function of density
Script 
If we introduce the gas equation written with the pressure ($p$), the volume ($V$), the mass ($M$), the specific gas constant ($R_s$), and the absolute temperature ($T$) as:
| $ p V = M R_s T $ |
and use the definition the density ($\rho$) given by:
| $ \rho \equiv\displaystyle\frac{ M }{ V }$ |
we can derive a specific equation for gases as follows:
| $ p = \rho R_s T $ |
ID:(15686, 0)
General Law of Ideal Gases
Storyboard 
The three gas laws (Boyle's Law, Charles's Law, Gay-Lussac's Law) and Avogadro's principle can be combined into a single law called the ideal gas law. This allows predicting the variation of one of the parameters that define the state of the gas (5224, 5226, 5177, and 9339) for an ideal gas, based on the initial state and any final state defined by the remaining three variables.
Variables
Calculations
Calculations
Equations
The pressure ($p$), the volume ($V$), the absolute temperature ($T$), and the number of moles ($n$) are related through the following physical laws:
• Boyle's law
• Charles's law
• Gay-Lussac's law
• Avogadro's law
These laws can be expressed in a more general form as:
$\displaystyle\frac{pV}{nT}=cte$
This general relationship states that the product of pressure and volume divided by the number of moles and temperature remains constant:
The pressure ($p$), the volume ($V$), the absolute temperature ($T$), and the number of moles ($n$) are related through the following physical laws:
• Boyle's law
• Charles's law
• Gay-Lussac's law
• Avogadro's law
These laws can be expressed in a more general form as:
$\displaystyle\frac{pV}{nT}=cte$
This general relationship states that the product of pressure and volume divided by the number of moles and temperature remains constant:
When the pressure ($p$) behaves as an ideal gas, satisfying the volume ($V$), the number of moles ($n$), the absolute temperature ($T$), and the universal gas constant ($R_C$), the ideal gas equation:
and the definition of the molar concentration ($c_m$):
lead to the following relationship:
When the pressure ($p$) behaves as an ideal gas, satisfying the volume ($V$), the number of moles ($n$), the absolute temperature ($T$), and the universal gas constant ($R_C$), the ideal gas equation:
and the definition of the molar concentration ($c_m$):
lead to the following relationship:
The pressure ($p$) is associated with the volume ($V$), ERROR:6679, the absolute temperature ($T$), and the universal gas constant ($R_C$) through the equation:
Since ERROR:6679 can be calculated with the mass ($M$) and the molar Mass ($M_m$) using:
and obtained with the definition of the specific gas constant ($R_s$) using:
we conclude that:
The pressure ($p$) is associated with the volume ($V$), ERROR:6679, the absolute temperature ($T$), and the universal gas constant ($R_C$) through the equation:
Since ERROR:6679 can be calculated with the mass ($M$) and the molar Mass ($M_m$) using:
and obtained with the definition of the specific gas constant ($R_s$) using:
we conclude that:
If we introduce the gas equation written with the pressure ($p$), the volume ($V$), the mass ($M$), the specific gas constant ($R_s$), and the absolute temperature ($T$) as:
and use the definition the density ($\rho$) given by:
we can derive a specific equation for gases as follows:
If we introduce the gas equation written with the pressure ($p$), the volume ($V$), the mass ($M$), the specific gas constant ($R_s$), and the absolute temperature ($T$) as:
and use the definition the density ($\rho$) given by:
we can derive a specific equation for gases as follows:
The ideal gas law is expressed as
and can be written as
$\displaystyle\frac{pV}{nT} = R$
This implies that the initial and final conditions must satisfy the equality
$\displaystyle\frac{p_iV_i}{n_iT_i} = R = \displaystyle\frac{p_fV_f}{n_fT_f}$
Thus, we obtain the following equation:
Examples
The universal gas law, also known as the ideal gas law, describes the relationship between the pressure, volume, temperature, and number of moles of a gas. It combines several gas laws, including Boyle's law, Charles's law, and Avogadro's principle, into a single equation. This law states that the product of the pressure and volume of a gas is directly proportional to the product of its temperature and the number of moles of gas. The ideal gas law assumes that gases are composed of a large number of molecules that are in constant, random motion and that the interactions between these molecules are negligible. This law is fundamental in predicting the behavior of gases under various conditions and is widely used in both scientific research and practical applications, such as engineering and chemistry.
The state of a system is described by the so-called equation of state, which establishes the relationship between the parameters that characterize the system.
In the case of gases, the parameters that describe their state are the pressure ($p$), the volume ($V$), the absolute temperature ($T$), and the number of moles ($n$). Typically, the latter parameter remains constant as it is associated with the amount of gas present.
The equation of state, therefore, relates pressure, volume, and temperature, and it establishes that there are only two degrees of freedom, as the equation of state allows for the calculation of the third parameter. In particular, if the volume is fixed, one can choose, for example, temperature as the variable, which enables the calculation of the corresponding pressure.
The three gas laws that relate to the pressure ($p$), the volume ($V$), and the absolute temperature ($T$) are:
• Boyle's Law, which states that at constant temperature, the product of the pressure and the volume of a gas is constant:
• Charles's Law, which states that at constant pressure, the volume of a gas is directly proportional to its absolute temperature:
• Gay-Lussac's Law, which states that at constant volume, the pressure of a gas is directly proportional to its absolute temperature:
These laws can be graphically represented as shown in the following image:
In 1834, mile Clapeyron [1] recognized that the pressure ($p$), the volume ($V$), the absolute temperature ($T$), and the number of moles ($n$) are related by Boyle's law, Charles's law, Gay-Lussac's law, and Avogadro's law. These laws can be expressed more generally as:
$\displaystyle\frac{pV}{nT} = \text{constant}$
This general relationship states that the product of pressure and volume divided by the number of moles and the temperature remains constant:
In this equation, the universal gas constant ($R_C$) assumes the value of 8.314 J/K mol.
[1] "M moire sur la puissance motrice de la chaleur" (Memoir on the Motive Power of Heat), mile Clapeyron, Journal de l' cole Polytechnique, 1834.
The ideal gas law is expressed as
and can be written as
$\displaystyle\frac{pV}{nT} = R$
This implies that the initial and final conditions must satisfy the equality
$\displaystyle\frac{p_iV_i}{n_iT_i} = R = \displaystyle\frac{p_fV_f}{n_fT_f}$
Thus, we obtain the following equation:
When the pressure ($p$) behaves as an ideal gas, satisfying the volume ($V$), the number of moles ($n$), the absolute temperature ($T$), and the universal gas constant ($R_C$), the ideal gas equation:
and the definition of the molar concentration ($c_m$):
lead to the following relationship:
The pressure ($p$) is associated with the volume ($V$), ERROR:6679, the absolute temperature ($T$), and the universal gas constant ($R_C$) through the equation:
Since ERROR:6679 can be calculated with the mass ($M$) and the molar Mass ($M_m$) using:
and obtained with the definition of the specific gas constant ($R_s$) using:
we conclude that:
If we introduce the gas equation written with the pressure ($p$), the volume ($V$), the mass ($M$), the specific gas constant ($R_s$), and the absolute temperature ($T$) as:
and use the definition the density ($\rho$) given by:
we can derive a specific equation for gases as follows:
The pressure ($p$), the volume ($V$), the absolute temperature ($T$), and the number of moles ($n$) are related by the following equation:
where the universal gas constant ($R_C$) has a value of 8.314 J/K mol.
The pressure ($p$), the volume ($V$), the absolute temperature ($T$), and the number of moles ($n$) are related by the following equation:
where the universal gas constant ($R_C$) has a value of 8.314 J/K mol.
For an initial state (the pressure in initial state ($p_i$), the volume in state i ($V_i$), the temperature in initial state ($T_i$), and the number of moles in state i ($n_i$)) and a final state (the pressure in final state ($p_f$), the volume in state f ($V_f$), the temperature in final state ($T_f$), and the number of moles in state f ($n_f$)), the following holds true:
The pressure ($p$) can be calculated from the molar concentration ($c_m$) using the absolute temperature ($T$), and the universal gas constant ($R_C$) as follows:
The pressure ($p$) can be calculated from the molar concentration ($c_m$) using the absolute temperature ($T$), and the universal gas constant ($R_C$) as follows:
The pressure ($p$) is related to the mass ($M$) with the volume ($V$), the specific gas constant ($R_s$), and the absolute temperature ($T$) through:
The pressure ($p$) is related to the mass ($M$) with the volume ($V$), the specific gas constant ($R_s$), and the absolute temperature ($T$) through:
When working with the specific data of a gas, the specific gas constant ($R_s$) can be defined in terms of the universal gas constant ($R_C$) and the molar Mass ($M_m$) as follows:
If we work with the mass or the density ($\rho$) of the gas, we can establish an equation analogous to that of ideal gases for the pressure ($p$) and the absolute temperature ($T$), with the only difference being that the constant will be specific to each type of gas and denoted as the specific gas constant ($R_s$):
If we work with the mass or the density ($\rho$) of the gas, we can establish an equation analogous to that of ideal gases for the pressure ($p$) and the absolute temperature ($T$), with the only difference being that the constant will be specific to each type of gas and denoted as the specific gas constant ($R_s$):
ID:(1476, 0)
