Benützer:


Allgemeines Gesetz der idealen Gase
Storyboard

Die drei Gasgesetze (Boyle-Mariottes Gesetz, Charles-Gesetz, Gay-Lussacs Gesetz) und das Avogadro-Prinzip können zu einem einzigen Gesetz kombiniert werden, das als das Gesetz der idealen Gase bezeichnet wird.

Dies ermöglicht es, die Variation eines der Parameter, die den Zustand des Gases definieren (die Druck ($p$), der Volumen ($V$), die Absolute Temperatur ($T$) und der Anzahl der Mol ($n$)), für ein ideales Gas vorherzusagen, basierend auf dem Anfangszustand und jedem Endzustand, der durch die verbleibenden drei Variablen definiert ist.

>Modell

ID:(1476, 0)


Mechanismen
Konzept

Das universelle Gasgesetz, auch bekannt als das ideale Gasgesetz, beschreibt die Beziehung zwischen Druck, Volumen, Temperatur und der Anzahl der Mole von einem Gas. Es kombiniert mehrere Gasgesetze, einschließlich des Boyle'schen Gesetzes, des Gesetzes von Charles und des Avogadro-Prinzips, in einer einzigen Gleichung. Dieses Gesetz besagt, dass das Produkt aus Druck und Volumen eines Gases direkt proportional zum Produkt aus Temperatur und der Anzahl der Mole des Gases ist. Das ideale Gasgesetz geht davon aus, dass Gase aus einer großen Anzahl von Molekülen bestehen, die sich in ständiger, zufälliger Bewegung befinden, und dass die Wechselwirkungen zwischen diesen Molekülen vernachlässigbar sind. Dieses Gesetz ist grundlegend, um das Verhalten von Gasen unter verschiedenen Bedingungen vorherzusagen, und wird sowohl in der wissenschaftlichen Forschung als auch in praktischen Anwendungen wie Ingenieurwesen und Chemie weit verbreitet verwendet.

ID:(15258, 0)


Gasgesetze
Konzept

Der Zustand eines Systems wird durch die sogenannte Zustandsgleichung beschrieben, die die Beziehung zwischen den Parametern festlegt, die das System charakterisieren.

Im Fall von Gasen sind die Parameter, die ihren Zustand beschreiben, die Druck ($p$), der Volumen ($V$), die Absolute Temperatur ($T$) und der Anzahl der Mol ($n$). In der Regel bleibt der letzte Parameter konstant, da er mit der Menge des vorhandenen Gases zusammenhängt.Die Zustandsgleichung verknüpft daher Druck, Volumen und Temperatur und legt fest, dass es nur zwei Freiheitsgrade gibt, da die Zustandsgleichung die Berechnung des dritten Parameters ermöglicht. Insbesondere, wenn das Volumen festgelegt ist, kann man beispielsweise die Temperatur als Variable wählen, was die Berechnung des entsprechenden Drucks ermöglicht.

ID:(587, 0)


Integration der Gasgesetze
Beschreibung

Die drei Gasgesetze, die mit die Druck ($p$), der Volumen ($V$) und die Absolute Temperatur ($T$) in Beziehung stehen, sind:

• Das Gesetz von Boyle, das besagt, dass bei konstanter Temperatur das Produkt aus Druck und Volumen eines Gases konstant ist:

$ p V = C_b $



• Das Gesetz von Charles, das besagt, dass bei konstantem Druck das Volumen eines Gases direkt proportional zur absoluten Temperatur ist:

$\displaystyle\frac{ V }{ T } = C_c$



• Das Gesetz von Gay-Lussac, das besagt, dass bei konstantem Volumen der Druck eines Gases direkt proportional zur absoluten Temperatur ist:

$\displaystyle\frac{ p }{ T } = C_g$



Diese Gesetze können graphisch wie in der folgenden Abbildung dargestellt werden:



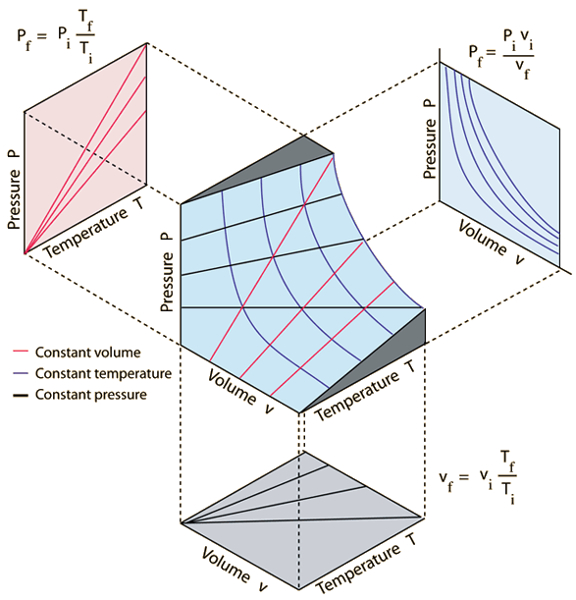
Im Jahr 1834 erkannte Émile Clapeyron [1], dass die Druck ($p$), der Volumen ($V$), die Absolute Temperatur ($T$) und der Anzahl der Mol ($n$) durch das Boyle'sche Gesetz, das Charles'sche Gesetz, das Gesetz von Gay-Lussac und das Avogadro-Gesetz miteinander verbunden sind. Diese Gesetze können allgemeiner ausgedrückt werden als:

$\displaystyle\frac{pV}{nT} = \text{konstant}$



Diese allgemeine Beziehung besagt, dass das Produkt von Druck und Volumen, geteilt durch die Anzahl der Mole und die Temperatur, konstant bleibt:

$ p V = n R_C T $



In dieser Gleichung nimmt die Universelle Gas Konstante ($R_C$) den Wert von 8,314 J/K·mol an.[1] "Mémoire sur la puissance motrice de la chaleur" (Abhandlung über die treibende Kraft der Wärme), Émile Clapeyron, Journal de l'École Polytechnique, 1834.

ID:(9525, 0)


Zustandsänderung eines idealen Gases nach dem allgemeinen Gasgesetz
Konzept

Das ideale Gasgesetz wird ausgedrückt als

$ p V = n R_C T $



und kann geschrieben werden als

$\displaystyle\frac{pV}{nT} = R$



Dies impliziert, dass die Anfangs- und Endbedingungen die Gleichheit erfüllen müssen

$\displaystyle\frac{p_iV_i}{n_iT_i} = R = \displaystyle\frac{p_fV_f}{n_fT_f}$



Somit erhalten wir die folgende Gleichung:

$\displaystyle\frac{ p_i V_i }{ n_i T_i }=\displaystyle\frac{ p_f V_f }{ n_f T_f }$

ID:(15683, 0)


Druck als Funktion der molaren Konzentration
Konzept

Wenn die Druck ($p$) sich wie ein ideales Gas verhält und der Volumen ($V$), der Anzahl der Mol ($n$), die Absolute Temperatur ($T$) und die Universelle Gas Konstante ($R_C$) erfüllt, führt die ideale Gasgleichung:

$ p V = n R_C T $



und die Definition von die Molare Konzentration ($c_m$):

$ c_m \equiv\displaystyle\frac{ n }{ V }$



zu folgender Beziehung:

$ p = c_m R_C T $

ID:(15684, 0)


Spezifisches Gasgesetz
Konzept

Die Druck ($p$) ist durch die Gleichung mit der Volumen ($V$), ERROR:6679, die Absolute Temperatur ($T$) und die Universelle Gas Konstante ($R_C$) verbunden:

$ p V = n R_C T $



Da ERROR:6679 mit die Masse ($M$) und die Molmasse ($M_m$) berechnet werden kann mittels:

$ n = \displaystyle\frac{ M }{ M_m }$



und durch die Definition von die Spezifische Gaskonstante ($R_s$) mit:

$ R_s \equiv \displaystyle\frac{ R_C }{ M_m }$



folgern wir:

$ p V = M R_s T $

ID:(15685, 0)


Druck als Funktion der Dichte
Konzept

Wenn wir die Gleichung für Gase einführen, die mit die Druck ($p$), der Volumen ($V$), die Masse ($M$), die Spezifische Gaskonstante ($R_s$) und die Absolute Temperatur ($T$) geschrieben ist als:

$ p V = M R_s T $



und die Definition die Dichte ($\rho$) verwenden, die gegeben ist durch:

$ \rho \equiv\displaystyle\frac{ M }{ V }$



können wir eine spezifische Gleichung für Gase ableiten, wie folgt:

$ p = \rho R_s T $

ID:(15686, 0)


Modell
Konzept


ID:(15317, 0)


Allgemeines Gesetz der idealen Gase
Modell

Die drei Gasgesetze (Boyle-Mariottes Gesetz, Charles-Gesetz, Gay-Lussacs Gesetz) und das Avogadro-Prinzip können zu einem einzigen Gesetz kombiniert werden, das als das Gesetz der idealen Gase bezeichnet wird. Dies ermöglicht es, die Variation eines der Parameter, die den Zustand des Gases definieren (5224, 5226, 5177 und 9339), für ein ideales Gas vorherzusagen, basierend auf dem Anfangszustand und jedem Endzustand, der durch die verbleibenden drei Variablen definiert ist.

Variablen
Symbol
Text
Variable
Wert
Einheiten
Berechnen
MKS-Wert
MKS-Einheiten
$c_i$
c_i
Anfängliche molare Konzentration
mol/m^3
$n_f$
n_f
Anzahl der Maulwürfe im Staat f
-
$n_i$
n_i
Anzahl der Maulwürfe im Staat i
-
$\rho_f$
rho_f
Dichte im Zustand f
kg/m^3
$\rho_i$
rho_i
Dichte im Zustand i
kg/m^3
$p_i$
p_i
Druck im Ausgangszustand
Pa
$p_f$
p_f
Druck im Endzustand
Pa
$c_f$
c_f
Endgültige molare Konzentration
mol/m^3
$M_f$
M_f
Messe im Staat f
kg
$M_i$
M_i
Messe im Staat i
kg
$M_m$
M_m
Molmasse
kg/mol
$R_s$
R_s
Spezifische Gaskonstante
J/kg K
$T_i$
T_i
Temperatur im Ausgangszustand
K
$T_f$
T_f
Temperatur im Endzustand
K
$V_f$
V_f
Volumen im Zustand f
m^3
$V_i$
V_i
Volumen im Zustand i
m^3

Berechnungen

Zuerst die Gleichung auswählen:   zu ,  dann die Variable auswählen:   zu 
Symbol
Gleichung
Gelöst
Übersetzt

Berechnungen

Symbol
Gleichung
Gelöst
Übersetzt

 Variable   Gegeben   Berechnen   Ziel :   Gleichung   Zu verwenden


Gleichungen

Die Druck ($p$), der Volumen ($V$), die Absolute Temperatur ($T$) und der Anzahl der Mol ($n$) stehen im Zusammenhang mit den folgenden physikalischen Gesetzen:

• Das Gesetz von Boyle

$ p V = C_b $



• Das Gesetz von Charles

$\displaystyle\frac{ V }{ T } = C_c$



• Das Gesetz von Gay-Lussac

$\displaystyle\frac{ p }{ T } = C_g$



• Das Gesetz von Avogadro

$\displaystyle\frac{ n }{ V } = C_a $



Diese Gesetze k nnen in einer allgemeineren Form ausgedr ckt werden:

$\displaystyle\frac{pV}{nT}=cte$



Diese allgemeine Beziehung besagt, dass das Produkt aus Druck und Volumen durch die Anzahl der Mol und die Temperatur geteilt konstant bleibt:

$ p V = n R_C T $

(ID 3183)

Die Druck ($p$), der Volumen ($V$), die Absolute Temperatur ($T$) und der Anzahl der Mol ($n$) stehen im Zusammenhang mit den folgenden physikalischen Gesetzen:

• Das Gesetz von Boyle

$ p V = C_b $



• Das Gesetz von Charles

$\displaystyle\frac{ V }{ T } = C_c$



• Das Gesetz von Gay-Lussac

$\displaystyle\frac{ p }{ T } = C_g$



• Das Gesetz von Avogadro

$\displaystyle\frac{ n }{ V } = C_a $



Diese Gesetze k nnen in einer allgemeineren Form ausgedr ckt werden:

$\displaystyle\frac{pV}{nT}=cte$



Diese allgemeine Beziehung besagt, dass das Produkt aus Druck und Volumen durch die Anzahl der Mol und die Temperatur geteilt konstant bleibt:

$ p V = n R_C T $

(ID 3183)

Wenn die Druck ($p$) sich wie ein ideales Gas verh lt und der Volumen ($V$), der Anzahl der Mol ($n$), die Absolute Temperatur ($T$) und die Universelle Gas Konstante ($R_C$) erf llt, f hrt die ideale Gasgleichung:

$ p V = n R_C T $



und die Definition von die Molare Konzentration ($c_m$):

$ c_m \equiv\displaystyle\frac{ n }{ V }$



zu folgender Beziehung:

$ p = c_m R_C T $

(ID 4479)

Wenn die Druck ($p$) sich wie ein ideales Gas verh lt und der Volumen ($V$), der Anzahl der Mol ($n$), die Absolute Temperatur ($T$) und die Universelle Gas Konstante ($R_C$) erf llt, f hrt die ideale Gasgleichung:

$ p V = n R_C T $



und die Definition von die Molare Konzentration ($c_m$):

$ c_m \equiv\displaystyle\frac{ n }{ V }$



zu folgender Beziehung:

$ p = c_m R_C T $

(ID 4479)

Die Druck ($p$) ist durch die Gleichung mit der Volumen ($V$), ERROR:6679, die Absolute Temperatur ($T$) und die Universelle Gas Konstante ($R_C$) verbunden:

$ p V = n R_C T $



Da ERROR:6679 mit die Masse ($M$) und die Molmasse ($M_m$) berechnet werden kann mittels:

$ n = \displaystyle\frac{ M }{ M_m }$



und durch die Definition von die Spezifische Gaskonstante ($R_s$) mit:

$ R_s \equiv \displaystyle\frac{ R_C }{ M_m }$



folgern wir:

$ p V = M R_s T $

(ID 8831)

Die Druck ($p$) ist durch die Gleichung mit der Volumen ($V$), ERROR:6679, die Absolute Temperatur ($T$) und die Universelle Gas Konstante ($R_C$) verbunden:

$ p V = n R_C T $



Da ERROR:6679 mit die Masse ($M$) und die Molmasse ($M_m$) berechnet werden kann mittels:

$ n = \displaystyle\frac{ M }{ M_m }$



und durch die Definition von die Spezifische Gaskonstante ($R_s$) mit:

$ R_s \equiv \displaystyle\frac{ R_C }{ M_m }$



folgern wir:

$ p V = M R_s T $

(ID 8831)

Wenn wir die Gleichung f r Gase einf hren, die mit die Druck ($p$), der Volumen ($V$), die Masse ($M$), die Spezifische Gaskonstante ($R_s$) und die Absolute Temperatur ($T$) geschrieben ist als:

$ p V = M R_s T $



und die Definition die Dichte ($\rho$) verwenden, die gegeben ist durch:

$ \rho \equiv\displaystyle\frac{ M }{ V }$



k nnen wir eine spezifische Gleichung f r Gase ableiten, wie folgt:

$ p = \rho R_s T $

(ID 8833)

Wenn wir die Gleichung f r Gase einf hren, die mit die Druck ($p$), der Volumen ($V$), die Masse ($M$), die Spezifische Gaskonstante ($R_s$) und die Absolute Temperatur ($T$) geschrieben ist als:

$ p V = M R_s T $



und die Definition die Dichte ($\rho$) verwenden, die gegeben ist durch:

$ \rho \equiv\displaystyle\frac{ M }{ V }$



k nnen wir eine spezifische Gleichung f r Gase ableiten, wie folgt:

$ p = \rho R_s T $

(ID 8833)

Das ideale Gasgesetz wird ausgedr ckt als

$ p V = n R_C T $



und kann geschrieben werden als

$\displaystyle\frac{pV}{nT} = R$



Dies impliziert, dass die Anfangs- und Endbedingungen die Gleichheit erf llen m ssen

$\displaystyle\frac{p_iV_i}{n_iT_i} = R = \displaystyle\frac{p_fV_f}{n_fT_f}$



Somit erhalten wir die folgende Gleichung:

$\displaystyle\frac{ p_i V_i }{ n_i T_i }=\displaystyle\frac{ p_f V_f }{ n_f T_f }$

(ID 9526)

Beispiele

Das universelle Gasgesetz, auch bekannt als das ideale Gasgesetz, beschreibt die Beziehung zwischen Druck, Volumen, Temperatur und der Anzahl der Mole von einem Gas. Es kombiniert mehrere Gasgesetze, einschlie lich des Boyle'schen Gesetzes, des Gesetzes von Charles und des Avogadro-Prinzips, in einer einzigen Gleichung. Dieses Gesetz besagt, dass das Produkt aus Druck und Volumen eines Gases direkt proportional zum Produkt aus Temperatur und der Anzahl der Mole des Gases ist. Das ideale Gasgesetz geht davon aus, dass Gase aus einer gro en Anzahl von Molek len bestehen, die sich in st ndiger, zuf lliger Bewegung befinden, und dass die Wechselwirkungen zwischen diesen Molek len vernachl ssigbar sind. Dieses Gesetz ist grundlegend, um das Verhalten von Gasen unter verschiedenen Bedingungen vorherzusagen, und wird sowohl in der wissenschaftlichen Forschung als auch in praktischen Anwendungen wie Ingenieurwesen und Chemie weit verbreitet verwendet.

(ID 15258)

Der Zustand eines Systems wird durch die sogenannte Zustandsgleichung beschrieben, die die Beziehung zwischen den Parametern festlegt, die das System charakterisieren.

Im Fall von Gasen sind die Parameter, die ihren Zustand beschreiben, die Druck ($p$), der Volumen ($V$), die Absolute Temperatur ($T$) und der Anzahl der Mol ($n$). In der Regel bleibt der letzte Parameter konstant, da er mit der Menge des vorhandenen Gases zusammenh ngt.Die Zustandsgleichung verkn pft daher Druck, Volumen und Temperatur und legt fest, dass es nur zwei Freiheitsgrade gibt, da die Zustandsgleichung die Berechnung des dritten Parameters erm glicht. Insbesondere, wenn das Volumen festgelegt ist, kann man beispielsweise die Temperatur als Variable w hlen, was die Berechnung des entsprechenden Drucks erm glicht.

(ID 587)

Die drei Gasgesetze, die mit die Druck ($p$), der Volumen ($V$) und die Absolute Temperatur ($T$) in Beziehung stehen, sind:

• Das Gesetz von Boyle, das besagt, dass bei konstanter Temperatur das Produkt aus Druck und Volumen eines Gases konstant ist:

$ p V = C_b $



• Das Gesetz von Charles, das besagt, dass bei konstantem Druck das Volumen eines Gases direkt proportional zur absoluten Temperatur ist:

$\displaystyle\frac{ V }{ T } = C_c$



• Das Gesetz von Gay-Lussac, das besagt, dass bei konstantem Volumen der Druck eines Gases direkt proportional zur absoluten Temperatur ist:

$\displaystyle\frac{ p }{ T } = C_g$



Diese Gesetze k nnen graphisch wie in der folgenden Abbildung dargestellt werden:



Im Jahr 1834 erkannte mile Clapeyron [1], dass die Druck ($p$), der Volumen ($V$), die Absolute Temperatur ($T$) und der Anzahl der Mol ($n$) durch das Boyle'sche Gesetz, das Charles'sche Gesetz, das Gesetz von Gay-Lussac und das Avogadro-Gesetz miteinander verbunden sind. Diese Gesetze k nnen allgemeiner ausgedr ckt werden als:

$\displaystyle\frac{pV}{nT} = \text{konstant}$



Diese allgemeine Beziehung besagt, dass das Produkt von Druck und Volumen, geteilt durch die Anzahl der Mole und die Temperatur, konstant bleibt:

$ p V = n R_C T $



In dieser Gleichung nimmt die Universelle Gas Konstante ($R_C$) den Wert von 8,314 J/K mol an.[1] "M moire sur la puissance motrice de la chaleur" (Abhandlung ber die treibende Kraft der W rme), mile Clapeyron, Journal de l' cole Polytechnique, 1834.

(ID 9525)

Das ideale Gasgesetz wird ausgedr ckt als

$ p V = n R_C T $



und kann geschrieben werden als

$\displaystyle\frac{pV}{nT} = R$



Dies impliziert, dass die Anfangs- und Endbedingungen die Gleichheit erf llen m ssen

$\displaystyle\frac{p_iV_i}{n_iT_i} = R = \displaystyle\frac{p_fV_f}{n_fT_f}$



Somit erhalten wir die folgende Gleichung:

$\displaystyle\frac{ p_i V_i }{ n_i T_i }=\displaystyle\frac{ p_f V_f }{ n_f T_f }$

(ID 15683)

Wenn die Druck ($p$) sich wie ein ideales Gas verh lt und der Volumen ($V$), der Anzahl der Mol ($n$), die Absolute Temperatur ($T$) und die Universelle Gas Konstante ($R_C$) erf llt, f hrt die ideale Gasgleichung:

$ p V = n R_C T $



und die Definition von die Molare Konzentration ($c_m$):

$ c_m \equiv\displaystyle\frac{ n }{ V }$



zu folgender Beziehung:

$ p = c_m R_C T $

(ID 15684)

Die Druck ($p$) ist durch die Gleichung mit der Volumen ($V$), ERROR:6679, die Absolute Temperatur ($T$) und die Universelle Gas Konstante ($R_C$) verbunden:

$ p V = n R_C T $



Da ERROR:6679 mit die Masse ($M$) und die Molmasse ($M_m$) berechnet werden kann mittels:

$ n = \displaystyle\frac{ M }{ M_m }$



und durch die Definition von die Spezifische Gaskonstante ($R_s$) mit:

$ R_s \equiv \displaystyle\frac{ R_C }{ M_m }$



folgern wir:

$ p V = M R_s T $

(ID 15685)

Wenn wir die Gleichung f r Gase einf hren, die mit die Druck ($p$), der Volumen ($V$), die Masse ($M$), die Spezifische Gaskonstante ($R_s$) und die Absolute Temperatur ($T$) geschrieben ist als:

$ p V = M R_s T $



und die Definition die Dichte ($\rho$) verwenden, die gegeben ist durch:

$ \rho \equiv\displaystyle\frac{ M }{ V }$



k nnen wir eine spezifische Gleichung f r Gase ableiten, wie folgt:

$ p = \rho R_s T $

(ID 15686)


(ID 15317)

ID:(1476, 0)