Utilisateur:


Loi générale des gaz parfaits
Storyboard

Les trois lois des gaz (loi de Boyle-Mariotte, loi de Charles, loi de Gay-Lussac) et le principe d'Avogadro peuvent être combinés en une seule loi appelée la loi des gaz parfaits.

Cela permet de prédire la variation de l'un des paramètres qui définissent l'état du gaz (a pression ($p$), le volume ($V$), a température absolue ($T$) et le nombre de taupes ($n$)) pour un gaz parfait, en fonction de l'état initial et de tout état final défini par les trois variables restantes.

>Modèle

ID:(1476, 0)


Mécanismes
Concept

La loi universelle des gaz, également connue sous le nom de loi des gaz parfaits, décrit la relation entre la pression, le volume, la température et le nombre de moles d'un gaz. Elle combine plusieurs lois des gaz, y compris la loi de Boyle, la loi de Charles et le principe d'Avogadro, en une seule équation. Cette loi stipule que le produit de la pression et du volume d'un gaz est directement proportionnel au produit de sa température et du nombre de moles de gaz. La loi des gaz parfaits suppose que les gaz sont constitués d'un grand nombre de molécules en mouvement constant et aléatoire, et que les interactions entre ces molécules sont négligeables. Cette loi est fondamentale pour prédire le comportement des gaz dans diverses conditions et est largement utilisée tant dans la recherche scientifique que dans des applications pratiques, comme l'ingénierie et la chimie.

ID:(15258, 0)


Lois sur les gaz
Concept

L'état d'un système est décrit par ce que l'on appelle l'équation d'état, qui établit la relation entre les paramètres caractérisant ce système.

Dans le cas des gaz, les paramètres décrivant leur état sont a pression ($p$), le volume ($V$), a température absolue ($T$), et le nombre de taupes ($n$). Généralement, le dernier paramètre reste constant car il est associé à la quantité de gaz présente.L'équation d'état relie donc la pression, le volume et la température, et établit qu'il n'y a que deux degrés de liberté, car l'équation d'état permet de calculer le troisième paramètre. En particulier, si le volume est fixé, on peut choisir, par exemple, la température comme variable, ce qui permet de calculer la pression correspondante.

ID:(587, 0)


Intégration des lois des gaz
Description

Les trois lois des gaz qui sont liées à A pression ($p$), le volume ($V$) et a température absolue ($T$) sont les suivantes :

• La loi de Boyle, qui stipule qu'à température constante, le produit de la pression et du volume d'un gaz est constant :

$ p V = C_b $



• La loi de Charles, qui stipule qu'à pression constante, le volume d'un gaz est directement proportionnel à sa température absolue :

$\displaystyle\frac{ V }{ T } = C_c$



• La loi de Gay-Lussac, qui stipule qu'à volume constant, la pression d'un gaz est directement proportionnelle à sa température absolue :

$\displaystyle\frac{ p }{ T } = C_g$



Ces lois peuvent être représentées graphiquement comme illustré dans l'image suivante :



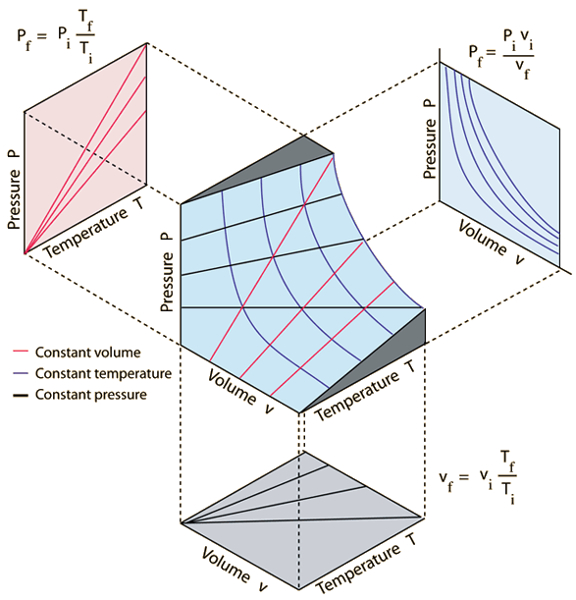
En 1834, Émile Clapeyron [1] a reconnu que a pression ($p$), le volume ($V$), a température absolue ($T$) et le nombre de taupes ($n$) sont liés par la loi de Boyle, la loi de Charles, la loi de Gay-Lussac et la loi d'Avogadro. Ces lois peuvent être exprimées de manière plus générale comme suit :

$\displaystyle\frac{pV}{nT} = \text{constante}$



Cette relation générale indique que le produit de la pression et du volume divisé par le nombre de moles et la température reste constant :

$ p V = n R_C T $



Dans cette équation, a constante du gaz universel ($R_C$) prend la valeur de 8,314 J/K·mol.[1] "Mémoire sur la puissance motrice de la chaleur", Émile Clapeyron, Journal de l'École Polytechnique, 1834.

ID:(9525, 0)


Changement d'état d'un gaz parfait selon la loi générale des gaz
Concept

La loi des gaz parfaits est exprimée comme

$ p V = n R_C T $



et peut être écrite comme

$\displaystyle\frac{pV}{nT} = R$



Cela implique que les conditions initiales et finales doivent satisfaire l'égalité

$\displaystyle\frac{p_iV_i}{n_iT_i} = R = \displaystyle\frac{p_fV_f}{n_fT_f}$



Ainsi, nous obtenons l'équation suivante:

$\displaystyle\frac{ p_i V_i }{ n_i T_i }=\displaystyle\frac{ p_f V_f }{ n_f T_f }$

ID:(15683, 0)


Pression en fonction de la concentration molaire
Concept

Quand a pression ($p$) se comporte comme un gaz idéal, en satisfaisant le volume ($V$), le nombre de taupes ($n$), a température absolue ($T$) et a constante du gaz universel ($R_C$), l'équation des gaz idéaux :

$ p V = n R_C T $



et la définition de a concentration molaire ($c_m$) :

$ c_m \equiv\displaystyle\frac{ n }{ V }$



conduisent à la relation suivante :

$ p = c_m R_C T $

ID:(15684, 0)


Loi spécifique sur les gaz
Concept

A pression ($p$) est associé à Le volume ($V$), ERROR:6679, a température absolue ($T$) et a constante du gaz universel ($R_C$) par l'équation :

$ p V = n R_C T $



Puisque ERROR:6679 peut être calculé avec a masse ($M$) et a masse molaire ($M_m$) en utilisant :

$ n = \displaystyle\frac{ M }{ M_m }$



et obtenu avec la définition de a constante de gaz spécifique ($R_s$) en utilisant :

$ R_s \equiv \displaystyle\frac{ R_C }{ M_m }$



nous concluons que :

$$

ID:(15685, 0)


Pression en fonction de la densité
Concept

Si nous introduisons l'équation des gaz écrite avec a pression ($p$), le volume ($V$), a masse ($M$), a constante de gaz spécifique ($R_s$) et a température absolue ($T$) comme suit :

$ p V = M R_s T $



et utilisons la définition a densité ($\rho$) donnée par :

$ \rho \equiv\displaystyle\frac{ M }{ V }$



nous pouvons dériver une équation spécifique pour les gaz comme suit :

$ p = \rho R_s T $

ID:(15686, 0)


Modèle
Concept


ID:(15317, 0)


Loi générale des gaz parfaits
Modèle

Les trois lois des gaz (loi de Boyle-Mariotte, loi de Charles, loi de Gay-Lussac) et le principe d'Avogadro peuvent être combinés en une seule loi appelée la loi des gaz parfaits. Cela permet de prédire la variation de l'un des paramètres qui définissent l'état du gaz (5224, 5226, 5177 et 9339) pour un gaz parfait, en fonction de l'état initial et de tout état final défini par les trois variables restantes.

Variables
Symbole
Texte
Variable
Valeur
Unités
Calculer
Valor MKS
Unités MKS
$c_f$
c_f
Concentration molaire finale
mol/m^3
$c_i$
c_i
Concentration molaire initiale
mol/m^3
$R_s$
R_s
Constante de gaz spécifique
J/kg K
$\rho_f$
rho_f
Densité dans l'état f
kg/m^3
$\rho_i$
rho_i
Densité dans l'état i
kg/m^3
$M_f$
M_f
Masse dans l'état f
kg
$M_i$
M_i
Masse dans l'état i
kg
$M_m$
M_m
Masse molaire
kg/mol
$n_f$
n_f
Nombre de taupes dans l'état f
-
$n_i$
n_i
Nombre de taupes dans l'état i
-
$p_f$
p_f
Pression à l'état final
Pa
$p_i$
p_i
Pression à l'état initial
Pa
$T_f$
T_f
Température à l'état final
K
$T_i$
T_i
Température à l'état initial
K
$V_f$
V_f
Volume à l'état f
m^3
$V_i$
V_i
Volume à l'état i
m^3

Calculs

D'abord, sélectionnez l'équation:   à ,  puis, sélectionnez la variable:   à 
Symbole
Équation
Résolu
Traduit

Calculs

Symbole
Équation
Résolu
Traduit

 Variable   Donnée   Calculer   Cible :   Équation   À utiliser


Équations

A pression ($p$), le volume ($V$), a température absolue ($T$) et le nombre de taupes ($n$) sont li s par les lois physiques suivantes :

• Loi de Boyle

$ p V = C_b $



• Loi de Charles

$\displaystyle\frac{ V }{ T } = C_c$



• Loi de Gay-Lussac

$\displaystyle\frac{ p }{ T } = C_g$



• Loi d'Avogadro

$\displaystyle\frac{ n }{ V } = C_a $



Ces lois peuvent tre exprim es de mani re plus g n rale comme suit :

$\displaystyle\frac{pV}{nT}=cte$



Cette relation g n rale tablit que le produit de la pression et du volume divis par le nombre de moles et la temp rature reste constant :

$ p V = n R_C T $

(ID 3183)

A pression ($p$), le volume ($V$), a température absolue ($T$) et le nombre de taupes ($n$) sont li s par les lois physiques suivantes :

• Loi de Boyle

$ p V = C_b $



• Loi de Charles

$\displaystyle\frac{ V }{ T } = C_c$



• Loi de Gay-Lussac

$\displaystyle\frac{ p }{ T } = C_g$



• Loi d'Avogadro

$\displaystyle\frac{ n }{ V } = C_a $



Ces lois peuvent tre exprim es de mani re plus g n rale comme suit :

$\displaystyle\frac{pV}{nT}=cte$



Cette relation g n rale tablit que le produit de la pression et du volume divis par le nombre de moles et la temp rature reste constant :

$ p V = n R_C T $

(ID 3183)

Quand a pression ($p$) se comporte comme un gaz id al, en satisfaisant le volume ($V$), le nombre de taupes ($n$), a température absolue ($T$) et a constante du gaz universel ($R_C$), l' quation des gaz id aux :

$ p V = n R_C T $



et la d finition de a concentration molaire ($c_m$) :

$ c_m \equiv\displaystyle\frac{ n }{ V }$



conduisent la relation suivante :

$ p = c_m R_C T $

(ID 4479)

Quand a pression ($p$) se comporte comme un gaz id al, en satisfaisant le volume ($V$), le nombre de taupes ($n$), a température absolue ($T$) et a constante du gaz universel ($R_C$), l' quation des gaz id aux :

$ p V = n R_C T $



et la d finition de a concentration molaire ($c_m$) :

$ c_m \equiv\displaystyle\frac{ n }{ V }$



conduisent la relation suivante :

$ p = c_m R_C T $

(ID 4479)

A pression ($p$) est associ le volume ($V$), ERROR:6679, a température absolue ($T$) et a constante du gaz universel ($R_C$) par l' quation :

$ p V = n R_C T $



Puisque ERROR:6679 peut tre calcul avec a masse ($M$) et a masse molaire ($M_m$) en utilisant :

$ n = \displaystyle\frac{ M }{ M_m }$



et obtenu avec la d finition de a constante de gaz spécifique ($R_s$) en utilisant :

$ R_s \equiv \displaystyle\frac{ R_C }{ M_m }$



nous concluons que :

$ p V = M R_s T $

(ID 8831)

A pression ($p$) est associ le volume ($V$), ERROR:6679, a température absolue ($T$) et a constante du gaz universel ($R_C$) par l' quation :

$ p V = n R_C T $



Puisque ERROR:6679 peut tre calcul avec a masse ($M$) et a masse molaire ($M_m$) en utilisant :

$ n = \displaystyle\frac{ M }{ M_m }$



et obtenu avec la d finition de a constante de gaz spécifique ($R_s$) en utilisant :

$ R_s \equiv \displaystyle\frac{ R_C }{ M_m }$



nous concluons que :

$ p V = M R_s T $

(ID 8831)

Si nous introduisons l' quation des gaz crite avec a pression ($p$), le volume ($V$), a masse ($M$), a constante de gaz spécifique ($R_s$) et a température absolue ($T$) comme suit :

$ p V = M R_s T $



et utilisons la d finition a densité ($\rho$) donn e par :

$ \rho \equiv\displaystyle\frac{ M }{ V }$



nous pouvons d river une quation sp cifique pour les gaz comme suit :

$ p = \rho R_s T $

(ID 8833)

Si nous introduisons l' quation des gaz crite avec a pression ($p$), le volume ($V$), a masse ($M$), a constante de gaz spécifique ($R_s$) et a température absolue ($T$) comme suit :

$ p V = M R_s T $



et utilisons la d finition a densité ($\rho$) donn e par :

$ \rho \equiv\displaystyle\frac{ M }{ V }$



nous pouvons d river une quation sp cifique pour les gaz comme suit :

$ p = \rho R_s T $

(ID 8833)

La loi des gaz parfaits est exprim e comme

$ p V = n R_C T $



et peut tre crite comme

$\displaystyle\frac{pV}{nT} = R$



Cela implique que les conditions initiales et finales doivent satisfaire l' galit

$\displaystyle\frac{p_iV_i}{n_iT_i} = R = \displaystyle\frac{p_fV_f}{n_fT_f}$



Ainsi, nous obtenons l' quation suivante:

$\displaystyle\frac{ p_i V_i }{ n_i T_i }=\displaystyle\frac{ p_f V_f }{ n_f T_f }$

(ID 9526)

Exemples

La loi universelle des gaz, galement connue sous le nom de loi des gaz parfaits, d crit la relation entre la pression, le volume, la temp rature et le nombre de moles d'un gaz. Elle combine plusieurs lois des gaz, y compris la loi de Boyle, la loi de Charles et le principe d'Avogadro, en une seule quation. Cette loi stipule que le produit de la pression et du volume d'un gaz est directement proportionnel au produit de sa temp rature et du nombre de moles de gaz. La loi des gaz parfaits suppose que les gaz sont constitu s d'un grand nombre de mol cules en mouvement constant et al atoire, et que les interactions entre ces mol cules sont n gligeables. Cette loi est fondamentale pour pr dire le comportement des gaz dans diverses conditions et est largement utilis e tant dans la recherche scientifique que dans des applications pratiques, comme l'ing nierie et la chimie.

(ID 15258)

L' tat d'un syst me est d crit par ce que l'on appelle l' quation d' tat, qui tablit la relation entre les param tres caract risant ce syst me.

Dans le cas des gaz, les param tres d crivant leur tat sont a pression ($p$), le volume ($V$), a température absolue ($T$), et le nombre de taupes ($n$). G n ralement, le dernier param tre reste constant car il est associ la quantit de gaz pr sente.L' quation d' tat relie donc la pression, le volume et la temp rature, et tablit qu'il n'y a que deux degr s de libert , car l' quation d' tat permet de calculer le troisi me param tre. En particulier, si le volume est fix , on peut choisir, par exemple, la temp rature comme variable, ce qui permet de calculer la pression correspondante.

(ID 587)

Les trois lois des gaz qui sont li es a pression ($p$), le volume ($V$) et a température absolue ($T$) sont les suivantes :

• La loi de Boyle, qui stipule qu' temp rature constante, le produit de la pression et du volume d'un gaz est constant :

$ p V = C_b $



• La loi de Charles, qui stipule qu' pression constante, le volume d'un gaz est directement proportionnel sa temp rature absolue :

$\displaystyle\frac{ V }{ T } = C_c$



• La loi de Gay-Lussac, qui stipule qu' volume constant, la pression d'un gaz est directement proportionnelle sa temp rature absolue :

$\displaystyle\frac{ p }{ T } = C_g$



Ces lois peuvent tre repr sent es graphiquement comme illustr dans l'image suivante :



En 1834, mile Clapeyron [1] a reconnu que a pression ($p$), le volume ($V$), a température absolue ($T$) et le nombre de taupes ($n$) sont li s par la loi de Boyle, la loi de Charles, la loi de Gay-Lussac et la loi d'Avogadro. Ces lois peuvent tre exprim es de mani re plus g n rale comme suit :

$\displaystyle\frac{pV}{nT} = \text{constante}$



Cette relation g n rale indique que le produit de la pression et du volume divis par le nombre de moles et la temp rature reste constant :

$ p V = n R_C T $



Dans cette quation, a constante du gaz universel ($R_C$) prend la valeur de 8,314 J/K mol.[1] "M moire sur la puissance motrice de la chaleur", mile Clapeyron, Journal de l' cole Polytechnique, 1834.

(ID 9525)

La loi des gaz parfaits est exprim e comme

$ p V = n R_C T $



et peut tre crite comme

$\displaystyle\frac{pV}{nT} = R$



Cela implique que les conditions initiales et finales doivent satisfaire l' galit

$\displaystyle\frac{p_iV_i}{n_iT_i} = R = \displaystyle\frac{p_fV_f}{n_fT_f}$



Ainsi, nous obtenons l' quation suivante:

$\displaystyle\frac{ p_i V_i }{ n_i T_i }=\displaystyle\frac{ p_f V_f }{ n_f T_f }$

(ID 15683)

Quand a pression ($p$) se comporte comme un gaz id al, en satisfaisant le volume ($V$), le nombre de taupes ($n$), a température absolue ($T$) et a constante du gaz universel ($R_C$), l' quation des gaz id aux :

$ p V = n R_C T $



et la d finition de a concentration molaire ($c_m$) :

$ c_m \equiv\displaystyle\frac{ n }{ V }$



conduisent la relation suivante :

$ p = c_m R_C T $

(ID 15684)

A pression ($p$) est associ le volume ($V$), ERROR:6679, a température absolue ($T$) et a constante du gaz universel ($R_C$) par l' quation :

$ p V = n R_C T $



Puisque ERROR:6679 peut tre calcul avec a masse ($M$) et a masse molaire ($M_m$) en utilisant :

$ n = \displaystyle\frac{ M }{ M_m }$



et obtenu avec la d finition de a constante de gaz spécifique ($R_s$) en utilisant :

$ R_s \equiv \displaystyle\frac{ R_C }{ M_m }$



nous concluons que :

$$

(ID 15685)

Si nous introduisons l' quation des gaz crite avec a pression ($p$), le volume ($V$), a masse ($M$), a constante de gaz spécifique ($R_s$) et a température absolue ($T$) comme suit :

$ p V = M R_s T $



et utilisons la d finition a densité ($\rho$) donn e par :

$ \rho \equiv\displaystyle\frac{ M }{ V }$



nous pouvons d river une quation sp cifique pour les gaz comme suit :

$ p = \rho R_s T $

(ID 15686)


(ID 15317)

ID:(1476, 0)