Utilizador:


Lei Geral dos Gases Ideais
Storyboard

As três leis dos gases (Lei de Boyle-Mariotte, Lei de Charles, Lei de Gay-Lussac) e o princípio de Avogadro podem ser combinados em uma única lei chamada de lei dos gases ideais.

Isso permite prever a variação de um dos parâmetros que definem o estado do gás (la pressão ($p$), o volume ($V$), la temperatura absoluta ($T$) e o número de moles ($n$)) para um gás ideal, com base no estado inicial e em qualquer estado final definido pelas três variáveis restantes.

>Modelo

ID:(1476, 0)


Mecanismos
Conceito

A lei universal dos gases, também conhecida como lei dos gases ideais, descreve a relação entre a pressão, o volume, a temperatura e o número de mols de um gás. Ela combina várias leis dos gases, incluindo a lei de Boyle, a lei de Charles e o princípio de Avogadro, em uma única equação. Esta lei estabelece que o produto da pressão e do volume de um gás é diretamente proporcional ao produto da sua temperatura e do número de mols de gás. A lei dos gases ideais assume que os gases são compostos por um grande número de moléculas em movimento constante e aleatório e que as interações entre essas moléculas são desprezíveis. Esta lei é fundamental para prever o comportamento dos gases em diversas condições e é amplamente utilizada tanto na pesquisa científica quanto em aplicações práticas, como engenharia e química.

ID:(15258, 0)


Leis do Gás
Conceito

O estado de um sistema é descrito pela chamada equação de estado, que estabelece a relação entre os parâmetros que caracterizam esse sistema.

No caso dos gases, os parâmetros que descrevem seu estado são la pressão ($p$), o volume ($V$), la temperatura absoluta ($T$) e o número de moles ($n$). Geralmente, o último parâmetro permanece constante, pois está associado à quantidade de gás presente.A equação de estado, portanto, relaciona pressão, volume e temperatura e estabelece que existem apenas dois graus de liberdade, já que a equação de estado permite o cálculo do terceiro parâmetro. Em particular, se o volume for fixado, é possível escolher, por exemplo, a temperatura como variável, o que permite calcular a pressão correspondente.

ID:(587, 0)


Integrando as leis dos gases
Descrição

As três leis dos gases que se relacionam com la pressão ($p$), o volume ($V$) e la temperatura absoluta ($T$) são:

• A Lei de Boyle, que estabelece que, à temperatura constante, o produto da pressão e do volume de um gás é constante:

$ p V = C_b $



• A Lei de Charles, que estabelece que, à pressão constante, o volume de um gás é diretamente proporcional à sua temperatura absoluta:

$\displaystyle\frac{ V }{ T } = C_c$



• A Lei de Gay-Lussac, que estabelece que, à volume constante, a pressão de um gás é diretamente proporcional à sua temperatura absoluta:

$\displaystyle\frac{ p }{ T } = C_g$



Essas leis podem ser representadas graficamente, como mostrado na seguinte imagem:



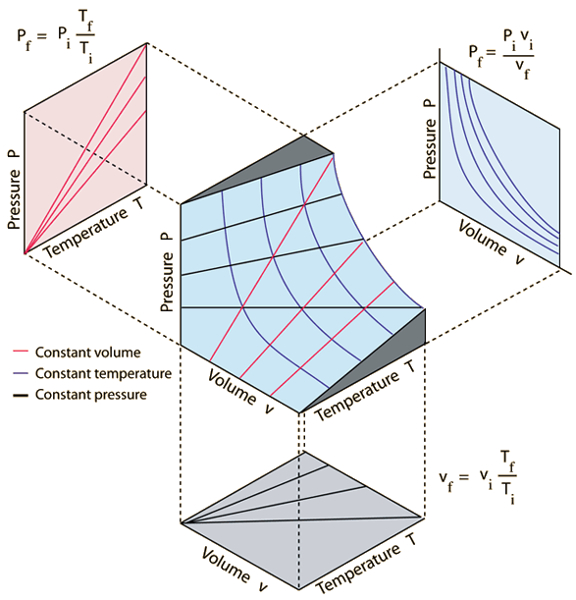
Em 1834, Émile Clapeyron [1] reconheceu que la pressão ($p$), o volume ($V$), la temperatura absoluta ($T$) e o número de moles ($n$) estão relacionados pela lei de Boyle, pela lei de Charles, pela lei de Gay-Lussac e pela lei de Avogadro. Essas leis podem ser expressas de forma mais geral como:

$\displaystyle\frac{pV}{nT} = \text{constante}$



Essa relação geral afirma que o produto da pressão e do volume, dividido pelo número de moles e pela temperatura, permanece constante:

$ p V = n R_C T $



Nessa equação, la constante de gás universal ($R_C$) assume o valor de 8,314 J/K·mol.[1] "Mémoire sur la puissance motrice de la chaleur" (Memória sobre o poder motriz do calor), Émile Clapeyron, Journal de l'École Polytechnique, 1834.

ID:(9525, 0)


Changement d'état d'un gaz parfait selon la loi générale des gaz
Conceito

A lei dos gases ideais é expressa como

$ p V = n R_C T $



e pode ser escrita como

$\displaystyle\frac{pV}{nT} = R$



Isso implica que as condições iniciais e finais devem satisfazer a igualdade

$\displaystyle\frac{p_iV_i}{n_iT_i} = R = \displaystyle\frac{p_fV_f}{n_fT_f}$



Assim, obtemos a seguinte equação:

$\displaystyle\frac{ p_i V_i }{ n_i T_i }=\displaystyle\frac{ p_f V_f }{ n_f T_f }$

ID:(15683, 0)


Pressão em função da concentração molar
Conceito

Quando la pressão ($p$) se comporta como um gás ideal, cumprindo com o volume ($V$), o número de moles ($n$), la temperatura absoluta ($T$) e la constante de gás universal ($R_C$), a equação dos gases ideais:

$ p V = n R_C T $



e a definição de la concentração molar ($c_m$):

$ c_m \equiv\displaystyle\frac{ n }{ V }$



levam à seguinte relação:

$ p = c_m R_C T $

ID:(15684, 0)


Lei específica do gás
Conceito

La pressão ($p$) está associado a o volume ($V$), ERROR:6679, la temperatura absoluta ($T$) e la constante de gás universal ($R_C$) através da equação:

$ p V = n R_C T $



Uma vez que ERROR:6679 pode ser calculado com la massa ($M$) e la massa molar ($M_m$) usando:

$ n = \displaystyle\frac{ M }{ M_m }$



e obtido com a definição de la constante específica de gás ($R_s$) usando:

$ R_s \equiv \displaystyle\frac{ R_C }{ M_m }$



concluímos que:

$ p V = M R_s T $

ID:(15685, 0)


Pressão em função da densidade
Conceito

Se introduzirmos a equação dos gases escrita com la pressão ($p$), o volume ($V$), la massa ($M$), la constante específica de gás ($R_s$) e la temperatura absoluta ($T$) como:

$ p V = M R_s T $



e usarmos a definição de la densidade ($\rho$) dada por:

$ \rho \equiv\displaystyle\frac{ M }{ V }$



podemos derivar uma equação específica para os gases da seguinte forma:

$ p = \rho R_s T $

ID:(15686, 0)


Modelo
Conceito


ID:(15317, 0)


Lei Geral dos Gases Ideais
Modelo

As três leis dos gases (Lei de Boyle-Mariotte, Lei de Charles, Lei de Gay-Lussac) e o princípio de Avogadro podem ser combinados em uma única lei chamada de lei dos gases ideais. Isso permite prever a variação de um dos parâmetros que definem o estado do gás (5224, 5226, 5177 e 9339) para um gás ideal, com base no estado inicial e em qualquer estado final definido pelas três variáveis restantes.

Variáveis
Símbolo
Texto
Variáve
Valor
Unidades
Calcular
Valeur MKS
Unidades MKS
$c_f$
c_f
Concentração molar final
mol/m^3
$c_i$
c_i
Concentração molar inicial
mol/m^3
$R_s$
R_s
Constante específica de gás
J/kg K
$\rho_f$
rho_f
Densidade no estado f
kg/m^3
$\rho_i$
rho_i
Densidade no estado i
kg/m^3
$M_m$
M_m
Massa molar
kg/mol
$M_f$
M_f
Missa no estado f
kg
$M_i$
M_i
Missa no estado i
kg
$n_f$
n_f
Número de moles no estado f
-
$n_i$
n_i
Número de moles no estado i
-
$p_f$
p_f
Pressão em estado final
Pa
$p_i$
p_i
Pressão no estado inicial
Pa
$T_f$
T_f
Temperatura no estado final
K
$T_i$
T_i
Temperatura no estado inicial
K
$V_f$
V_f
Volume no estado f
m^3
$V_i$
V_i
Volume no estado i
m^3

Cálculos

Primeiro, selecione a equação:   para ,  depois, selecione a variável:   para 
Símbolo
Equação
Resolvido
Traduzido

Cálculos

Símbolo
Equação
Resolvido
Traduzido

 Variáve   Dado   Calcular   Objetivo :   Equação   A ser usado


Equações

La pressão ($p$), o volume ($V$), la temperatura absoluta ($T$) e o número de moles ($n$) est o relacionados atrav s das seguintes leis f sicas:

• Lei de Boyle

$ p V = C_b $



• Lei de Charles

$\displaystyle\frac{ V }{ T } = C_c$



• Lei de Gay-Lussac

$\displaystyle\frac{ p }{ T } = C_g$



• Lei de Avogadro

$\displaystyle\frac{ n }{ V } = C_a $



Essas leis podem ser expressas de forma mais geral como:

$\displaystyle\frac{pV}{nT}=cte$



Essa rela o geral estabelece que o produto da press o e do volume dividido pelo n mero de moles e a temperatura permanece constante:

$ p V = n R_C T $

(ID 3183)

La pressão ($p$), o volume ($V$), la temperatura absoluta ($T$) e o número de moles ($n$) est o relacionados atrav s das seguintes leis f sicas:

• Lei de Boyle

$ p V = C_b $



• Lei de Charles

$\displaystyle\frac{ V }{ T } = C_c$



• Lei de Gay-Lussac

$\displaystyle\frac{ p }{ T } = C_g$



• Lei de Avogadro

$\displaystyle\frac{ n }{ V } = C_a $



Essas leis podem ser expressas de forma mais geral como:

$\displaystyle\frac{pV}{nT}=cte$



Essa rela o geral estabelece que o produto da press o e do volume dividido pelo n mero de moles e a temperatura permanece constante:

$ p V = n R_C T $

(ID 3183)

Quando la pressão ($p$) se comporta como um g s ideal, cumprindo com o volume ($V$), o número de moles ($n$), la temperatura absoluta ($T$) e la constante de gás universal ($R_C$), a equa o dos gases ideais:

$ p V = n R_C T $



e a defini o de la concentração molar ($c_m$):

$ c_m \equiv\displaystyle\frac{ n }{ V }$



levam seguinte rela o:

$ p = c_m R_C T $

(ID 4479)

Quando la pressão ($p$) se comporta como um g s ideal, cumprindo com o volume ($V$), o número de moles ($n$), la temperatura absoluta ($T$) e la constante de gás universal ($R_C$), a equa o dos gases ideais:

$ p V = n R_C T $



e a defini o de la concentração molar ($c_m$):

$ c_m \equiv\displaystyle\frac{ n }{ V }$



levam seguinte rela o:

$ p = c_m R_C T $

(ID 4479)

La pressão ($p$) est associado a o volume ($V$), ERROR:6679, la temperatura absoluta ($T$) e la constante de gás universal ($R_C$) atrav s da equa o:

$ p V = n R_C T $



Uma vez que ERROR:6679 pode ser calculado com la massa ($M$) e la massa molar ($M_m$) usando:

$ n = \displaystyle\frac{ M }{ M_m }$



e obtido com a defini o de la constante específica de gás ($R_s$) usando:

$ R_s \equiv \displaystyle\frac{ R_C }{ M_m }$



conclu mos que:

$ p V = M R_s T $

(ID 8831)

La pressão ($p$) est associado a o volume ($V$), ERROR:6679, la temperatura absoluta ($T$) e la constante de gás universal ($R_C$) atrav s da equa o:

$ p V = n R_C T $



Uma vez que ERROR:6679 pode ser calculado com la massa ($M$) e la massa molar ($M_m$) usando:

$ n = \displaystyle\frac{ M }{ M_m }$



e obtido com a defini o de la constante específica de gás ($R_s$) usando:

$ R_s \equiv \displaystyle\frac{ R_C }{ M_m }$



conclu mos que:

$ p V = M R_s T $

(ID 8831)

Se introduzirmos a equa o dos gases escrita com la pressão ($p$), o volume ($V$), la massa ($M$), la constante específica de gás ($R_s$) e la temperatura absoluta ($T$) como:

$ p V = M R_s T $



e usarmos a defini o de la densidade ($\rho$) dada por:

$ \rho \equiv\displaystyle\frac{ M }{ V }$



podemos derivar uma equa o espec fica para os gases da seguinte forma:

$ p = \rho R_s T $

(ID 8833)

Se introduzirmos a equa o dos gases escrita com la pressão ($p$), o volume ($V$), la massa ($M$), la constante específica de gás ($R_s$) e la temperatura absoluta ($T$) como:

$ p V = M R_s T $



e usarmos a defini o de la densidade ($\rho$) dada por:

$ \rho \equiv\displaystyle\frac{ M }{ V }$



podemos derivar uma equa o espec fica para os gases da seguinte forma:

$ p = \rho R_s T $

(ID 8833)

A lei dos gases ideais expressa como

$ p V = n R_C T $



e pode ser escrita como

$\displaystyle\frac{pV}{nT} = R$



Isso implica que as condi es iniciais e finais devem satisfazer a igualdade

$\displaystyle\frac{p_iV_i}{n_iT_i} = R = \displaystyle\frac{p_fV_f}{n_fT_f}$



Assim, obtemos a seguinte equa o:

$\displaystyle\frac{ p_i V_i }{ n_i T_i }=\displaystyle\frac{ p_f V_f }{ n_f T_f }$

(ID 9526)

Exemplos

A lei universal dos gases, tamb m conhecida como lei dos gases ideais, descreve a rela o entre a press o, o volume, a temperatura e o n mero de mols de um g s. Ela combina v rias leis dos gases, incluindo a lei de Boyle, a lei de Charles e o princ pio de Avogadro, em uma nica equa o. Esta lei estabelece que o produto da press o e do volume de um g s diretamente proporcional ao produto da sua temperatura e do n mero de mols de g s. A lei dos gases ideais assume que os gases s o compostos por um grande n mero de mol culas em movimento constante e aleat rio e que as intera es entre essas mol culas s o desprez veis. Esta lei fundamental para prever o comportamento dos gases em diversas condi es e amplamente utilizada tanto na pesquisa cient fica quanto em aplica es pr ticas, como engenharia e qu mica.

(ID 15258)

O estado de um sistema descrito pela chamada equa o de estado, que estabelece a rela o entre os par metros que caracterizam esse sistema.

No caso dos gases, os par metros que descrevem seu estado s o la pressão ($p$), o volume ($V$), la temperatura absoluta ($T$) e o número de moles ($n$). Geralmente, o ltimo par metro permanece constante, pois est associado quantidade de g s presente.A equa o de estado, portanto, relaciona press o, volume e temperatura e estabelece que existem apenas dois graus de liberdade, j que a equa o de estado permite o c lculo do terceiro par metro. Em particular, se o volume for fixado, poss vel escolher, por exemplo, a temperatura como vari vel, o que permite calcular a press o correspondente.

(ID 587)

As tr s leis dos gases que se relacionam com la pressão ($p$), o volume ($V$) e la temperatura absoluta ($T$) s o:

• A Lei de Boyle, que estabelece que, temperatura constante, o produto da press o e do volume de um g s constante:

$ p V = C_b $



• A Lei de Charles, que estabelece que, press o constante, o volume de um g s diretamente proporcional sua temperatura absoluta:

$\displaystyle\frac{ V }{ T } = C_c$



• A Lei de Gay-Lussac, que estabelece que, volume constante, a press o de um g s diretamente proporcional sua temperatura absoluta:

$\displaystyle\frac{ p }{ T } = C_g$



Essas leis podem ser representadas graficamente, como mostrado na seguinte imagem:



Em 1834, mile Clapeyron [1] reconheceu que la pressão ($p$), o volume ($V$), la temperatura absoluta ($T$) e o número de moles ($n$) est o relacionados pela lei de Boyle, pela lei de Charles, pela lei de Gay-Lussac e pela lei de Avogadro. Essas leis podem ser expressas de forma mais geral como:

$\displaystyle\frac{pV}{nT} = \text{constante}$



Essa rela o geral afirma que o produto da press o e do volume, dividido pelo n mero de moles e pela temperatura, permanece constante:

$ p V = n R_C T $



Nessa equa o, la constante de gás universal ($R_C$) assume o valor de 8,314 J/K mol.[1] "M moire sur la puissance motrice de la chaleur" (Mem ria sobre o poder motriz do calor), mile Clapeyron, Journal de l' cole Polytechnique, 1834.

(ID 9525)

A lei dos gases ideais expressa como

$ p V = n R_C T $



e pode ser escrita como

$\displaystyle\frac{pV}{nT} = R$



Isso implica que as condi es iniciais e finais devem satisfazer a igualdade

$\displaystyle\frac{p_iV_i}{n_iT_i} = R = \displaystyle\frac{p_fV_f}{n_fT_f}$



Assim, obtemos a seguinte equa o:

$\displaystyle\frac{ p_i V_i }{ n_i T_i }=\displaystyle\frac{ p_f V_f }{ n_f T_f }$

(ID 15683)

Quando la pressão ($p$) se comporta como um g s ideal, cumprindo com o volume ($V$), o número de moles ($n$), la temperatura absoluta ($T$) e la constante de gás universal ($R_C$), a equa o dos gases ideais:

$ p V = n R_C T $



e a defini o de la concentração molar ($c_m$):

$ c_m \equiv\displaystyle\frac{ n }{ V }$



levam seguinte rela o:

$ p = c_m R_C T $

(ID 15684)

La pressão ($p$) est associado a o volume ($V$), ERROR:6679, la temperatura absoluta ($T$) e la constante de gás universal ($R_C$) atrav s da equa o:

$ p V = n R_C T $



Uma vez que ERROR:6679 pode ser calculado com la massa ($M$) e la massa molar ($M_m$) usando:

$ n = \displaystyle\frac{ M }{ M_m }$



e obtido com a defini o de la constante específica de gás ($R_s$) usando:

$ R_s \equiv \displaystyle\frac{ R_C }{ M_m }$



conclu mos que:

$ p V = M R_s T $

(ID 15685)

Se introduzirmos a equa o dos gases escrita com la pressão ($p$), o volume ($V$), la massa ($M$), la constante específica de gás ($R_s$) e la temperatura absoluta ($T$) como:

$ p V = M R_s T $



e usarmos a defini o de la densidade ($\rho$) dada por:

$ \rho \equiv\displaystyle\frac{ M }{ V }$



podemos derivar uma equa o espec fica para os gases da seguinte forma:

$ p = \rho R_s T $

(ID 15686)


(ID 15317)

ID:(1476, 0)