Utilizador:
Aceleração constante, dois estágios
Storyboard
No caso de um movimento acelerado em duas etapas, quando se transita da primeira para a segunda aceleração, a velocidade final da primeira etapa se torna a velocidade inicial da segunda. O mesmo se aplica à posição, onde a posição final da primeira etapa é igual à posição inicial da segunda etapa.
Ao contrário do modelo de duas velocidades, este modelo não apresenta problemas de descontinuidade, exceto pelo fato de que a aceleração pode mudar abruptamente, o que é tecnicamente possível, mas muitas vezes não muito realista.
ID:(1435, 0)
Movimento em dois estágios
Conceito
Em um cenário de movimento em duas etapas, primeiro o objeto modifica sua velocidade em la diferença de velocidade na primeira etapa ($\Delta v_1$) durante um intervalo de tempo de um tempo decorrido na primeira etapa ($\Delta t_1$) com uma aceleração de uma aceleração durante a primeira fase ($a_1$).
$ a_1 \equiv\displaystyle\frac{ \Delta v_1 }{ \Delta t_1 }$
Posteriormente, na segunda etapa, ele avança modificando sua velocidade em la diferença de velocidade na segunda etapa ($\Delta v_2$) durante um intervalo de tempo de o tempo gasto na segunda etapa ($\Delta t_2$) com uma aceleração de la aceleração durante a segunda etapa ($a_2$).
$ a_2 \equiv\displaystyle\frac{ \Delta v_2 }{ \Delta t_2 }$
Ao representar isso graficamente, obtemos um diagrama de velocidade e tempo conforme mostrado abaixo:
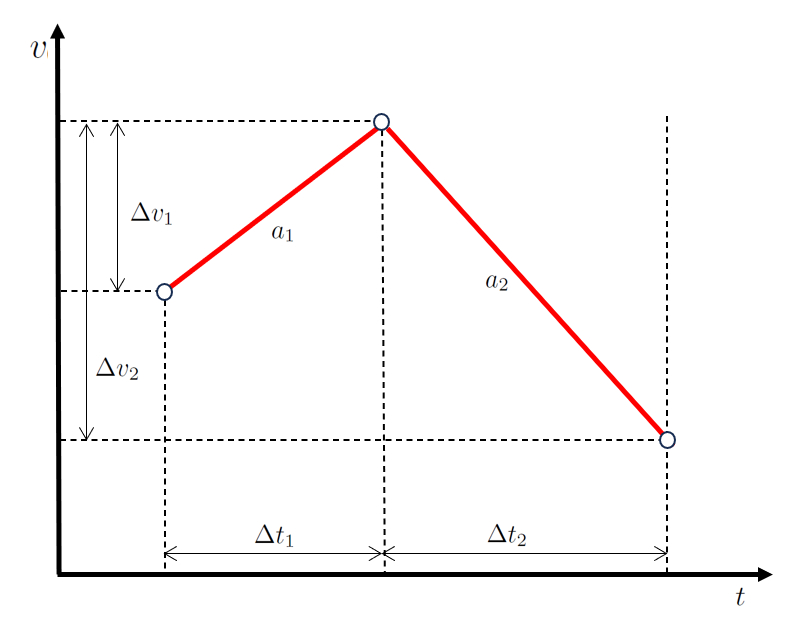
A chave aqui é que os valores o tempo decorrido na primeira etapa ($\Delta t_1$) e o tempo gasto na segunda etapa ($\Delta t_2$) são sequenciais, assim como os valores la diferença de velocidade na primeira etapa ($\Delta v_1$) e la diferença de velocidade na segunda etapa ($\Delta v_2$).
ID:(4829, 0)
Evolução da velocidade
Conceito
No caso de um movimento em duas etapas, a primeira etapa pode ser descrita por uma função que envolve os pontos o tempo inicial ($t_0$), o tempo final da primeira e início da segunda etapa ($t_1$), la velocidade inicial ($v_0$) e la velocidade do primeiro estágio ($v_1$), representada por uma reta com uma inclinação de la aceleração durante a primeira fase ($a_1$):
$ v_1 = v_0 + a_1 ( t_1 - t_0 )$
Para a segunda etapa, definida pelos pontos la velocidade do primeiro estágio ($v_1$), la velocidade do segundo estágio ($v_2$), o tempo final da primeira e início da segunda etapa ($t_1$) e o hora de término da segunda etapa ($t_2$), é empregada uma segunda reta com uma inclinação de la aceleração durante a segunda etapa ($a_2$):
$ v_2 = v_1 + a_2 ( t_2 - t_1 )$
que é representada como:
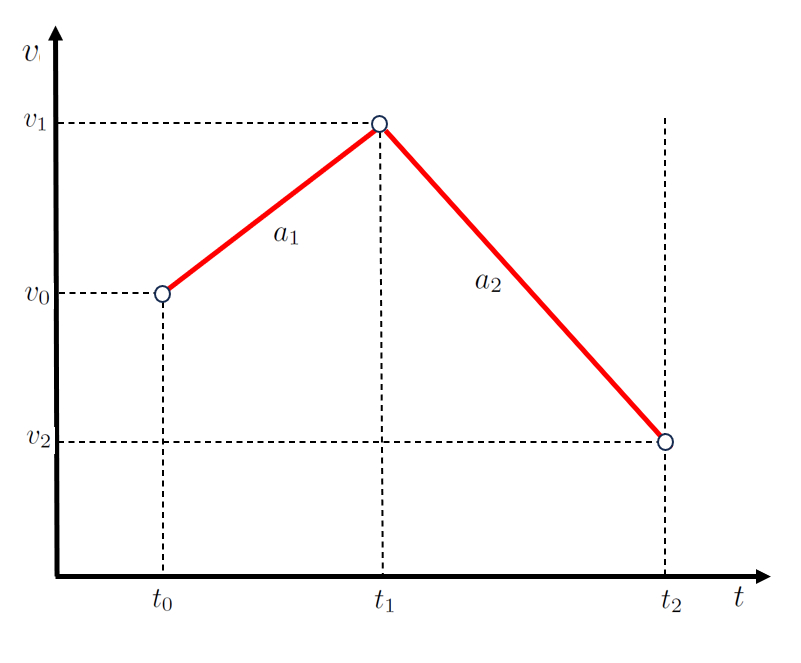
ID:(4357, 0)
Evolução da posição
Conceito
No caso de um movimento em duas etapas, a posição em que a primeira etapa termina coincide com a posição em que a segunda etapa começa ($s_1$).
Da mesma forma, o tempo em que a primeira etapa termina coincide com o tempo em que a segunda etapa começa ($t_1$).
Dado que o movimento é definido pela aceleração experimentada, a velocidade alcançada no final da primeira etapa deve corresponder à velocidade inicial da segunda etapa ($v_1$).
No caso de uma aceleração constante, na primeira etapa, o primeira posição final e largada na segunda etapa ($s_1$) depende de la velocidade ($s_0$), la velocidade inicial ($v_0$), la aceleração durante a primeira fase ($a_1$), o tempo final da primeira e início da segunda etapa ($t_1$) e o tempo inicial ($t_0$), como segue:
$ s_1 = s_0 + v_0 ( t_1 - t_0 )+\displaystyle\frac{1}{2} a_1 ( t_1 - t_0 )^2$
Na segunda etapa, la posição final da segunda fase ($s_2$) depende de o primeira posição final e largada na segunda etapa ($s_1$), la velocidade do primeiro estágio ($v_1$), la aceleração durante a segunda etapa ($a_2$), o tempo final da primeira e início da segunda etapa ($t_1$) e o hora de término da segunda etapa ($t_2$), como segue:
$ s_2 = s_1 + v_1 ( t_2 - t_1 )+\displaystyle\frac{1}{2} a_2 ( t_2 - t_1 )^2$
que é representado como:
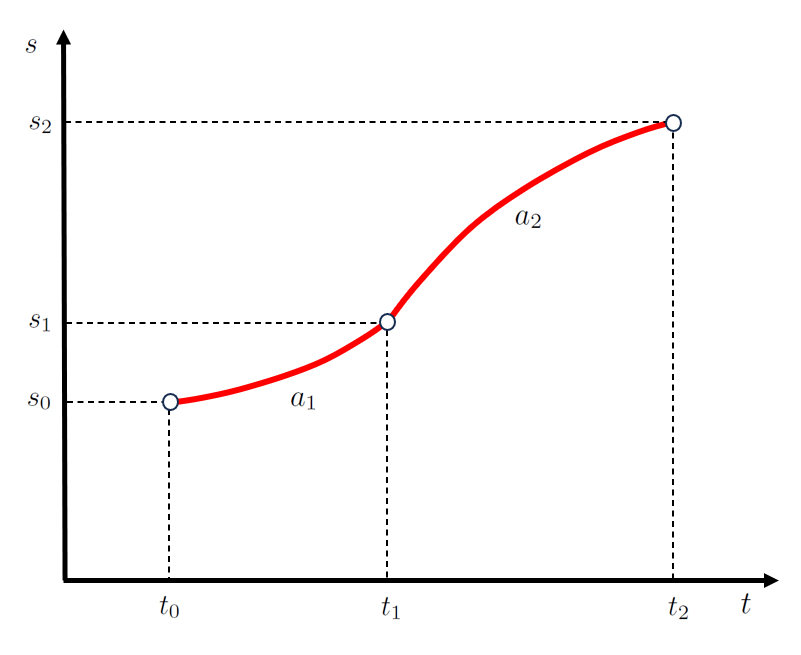
ID:(2254, 0)
Modelo
Conceito
Se o movimento envolve duas etapas com diferentes acelerações constantes $a_1$ e $a_2$:
• Começa em um tempo $t_0$ em uma posição $s_0$ com velocidade $v_0$.
• Termina em um tempo $t_2$ em uma posição $s_2$ com velocidade $v_2$.
A chave está na transição de uma etapa para outra:
• As velocidades variam de acordo com as acelerações, mas são iguais no ponto de transição entre as etapas ($v_1$).
• As posições variam de acordo com a velocidade, mas são iguais no ponto de transição entre as etapas ($s_1$).
• Os tempos são iguais no ponto de transição entre as etapas ($t_1$).
Isso é resumido nos seguintes gráficos:
As equações que satisfazem essas relações originam o seguinte modelo, que permite calcular qualquer cenário:
Variáveis
Parâmetros
Parâmetro selecionado
Cálculos
Equação
$ a_1 \equiv\displaystyle\frac{ \Delta v_1 }{ \Delta t_1 }$
a_m = Dv / Dt
$ a_2 \equiv\displaystyle\frac{ \Delta v_2 }{ \Delta t_2 }$
a_m = Dv / Dt
$ \Delta s_1 \equiv s_1 - s_0 $
Ds = s - s_0
$ \Delta s_2 \equiv s_2 - s_1 $
Ds = s - s_0
$ \Delta t_1 \equiv t_1 - t_0 $
Dt = t - t_0
$ \Delta t_2 \equiv t_2 - t_1 $
Dt = t - t_0
$ \Delta v_1 \equiv v_1 - v_0 $
Dv = v - v_0
$ \Delta v_2 \equiv v_2 - v_1 $
Dv = v - v_0
$ s_1 = s_0 + v_0 ( t_1 - t_0 )+\displaystyle\frac{1}{2} a_1 ( t_1 - t_0 )^2$
s = s_0 + v_0 * ( t - t_0 )+ a_0 *( t - t_0 )^2/2
$ s_2 = s_1 + v_1 ( t_2 - t_1 )+\displaystyle\frac{1}{2} a_2 ( t_2 - t_1 )^2$
s = s_0 + v_0 * ( t - t_0 )+ a_0 *( t - t_0 )^2/2
$ s_1 = s_0 +\displaystyle\frac{ v_1 ^2- v_0 ^2}{2 a_1 }$
s = s_0 +( v ^2- v_0 ^2)/(2* a_0 )
$ s_2 = s_1 +\displaystyle\frac{ v_2 ^2- v_1 ^2}{2 a_2 }$
s = s_0 +( v ^2- v_0 ^2)/(2* a_0 )
$ v_1 = v_0 + a_1 ( t_1 - t_0 )$
v = v_0 + a_0 *( t - t_0 )
$ v_2 = v_1 + a_2 ( t_2 - t_1 )$
v = v_0 + a_0 *( t - t_0 )
ID:(15400, 0)
Variação de velocidade (1)
Equação
A aceleração corresponde à variação da velocidade por unidade de tempo.
Portanto, é necessário definir la diferença de velocidade ($\Delta v$) em função de la velocidade ($v$) e la velocidade inicial ($v_0$) como:
 $ \Delta v_1 \equiv v_1 - v_0 $ |
 $ \Delta v \equiv v - v_0 $ |
ID:(4355, 1)
Variação de velocidade (2)
Equação
A aceleração corresponde à variação da velocidade por unidade de tempo.
Portanto, é necessário definir la diferença de velocidade ($\Delta v$) em função de la velocidade ($v$) e la velocidade inicial ($v_0$) como:
| $ \Delta v_2 \equiv v_2 - v_1 $ |
| $ \Delta v \equiv v - v_0 $ |
ID:(4355, 2)
Tempo decorrido (1)
Equação
Para descrever o movimento de um objeto, precisamos calcular o tempo decorrido. Essa magnitude é obtida medindo o tempo inicial e o tempo final do movimento. A duração é determinada subtraindo o tempo inicial do tempo final.
Isso é representado matematicamente como
| $ \Delta t_1 \equiv t_1 - t_0 $ |
| $ \Delta t \equiv t - t_0 $ |
onde $\Delta t$ é a duração, $t$ é o tempo final e $t_0$ é o tempo inicial.
ID:(4353, 1)
Tempo decorrido (2)
Equação
Para descrever o movimento de um objeto, precisamos calcular o tempo decorrido. Essa magnitude é obtida medindo o tempo inicial e o tempo final do movimento. A duração é determinada subtraindo o tempo inicial do tempo final.
Isso é representado matematicamente como
| $ \Delta t_2 \equiv t_2 - t_1 $ |
| $ \Delta t \equiv t - t_0 $ |
onde $\Delta t$ é a duração, $t$ é o tempo final e $t_0$ é o tempo inicial.
ID:(4353, 2)
Aceleração média (1)
Equação
A proporção na qual a variação da velocidade ao longo do tempo é definida como la aceleração média ($\bar{a}$). Para medi-la, é necessário observar la diferença de velocidade ($\Delta v$) e o tempo decorrido ($\Delta t$).
Um método comum para medir a aceleração média envolve o uso de uma lâmpada estroboscópica que ilumina o objeto em intervalos definidos. Ao tirar uma fotografia, pode-se determinar a distância percorrida pelo objeto nesse tempo. Calculando duas velocidades consecutivas, pode-se determinar sua variação e, com o tempo decorrido entre as fotos, a aceleração média.
A equação que descreve a aceleração média é a seguinte:
| $ a_1 \equiv\displaystyle\frac{ \Delta v_1 }{ \Delta t_1 }$ |
| $ \bar{a} \equiv\displaystyle\frac{ \Delta v }{ \Delta t }$ |
A definição de la aceleração média ($\bar{a}$) é considerada como a relação entre la diferença de velocidade ($\Delta v$) e o tempo decorrido ($\Delta t$). Ou seja,
| $ \Delta v \equiv v - v_0 $ |
e
| $ \Delta t \equiv t - t_0 $ |
A relação entre ambos é definida como la aceleração centrífuga ($a_c$)
| $ \bar{a} \equiv\displaystyle\frac{ \Delta v }{ \Delta t }$ |
dentro desse intervalo de tempo.
É importante notar que a aceleração média é uma estimativa da aceleração real.
O principal problema é que se a aceleração variar durante o tempo decorrido, o valor da aceleração média pode diferir muito da aceleração média real.
Portanto, a chave é
Determinar a aceleração em um período de tempo suficientemente curto para minimizar a variação.
ID:(3678, 1)
Aceleração média (2)
Equação
A proporção na qual a variação da velocidade ao longo do tempo é definida como la aceleração média ($\bar{a}$). Para medi-la, é necessário observar la diferença de velocidade ($\Delta v$) e o tempo decorrido ($\Delta t$).
Um método comum para medir a aceleração média envolve o uso de uma lâmpada estroboscópica que ilumina o objeto em intervalos definidos. Ao tirar uma fotografia, pode-se determinar a distância percorrida pelo objeto nesse tempo. Calculando duas velocidades consecutivas, pode-se determinar sua variação e, com o tempo decorrido entre as fotos, a aceleração média.
A equação que descreve a aceleração média é a seguinte:
| $ a_2 \equiv\displaystyle\frac{ \Delta v_2 }{ \Delta t_2 }$ |
| $ \bar{a} \equiv\displaystyle\frac{ \Delta v }{ \Delta t }$ |
A definição de la aceleração média ($\bar{a}$) é considerada como a relação entre la diferença de velocidade ($\Delta v$) e o tempo decorrido ($\Delta t$). Ou seja,
| $ \Delta v \equiv v - v_0 $ |
e
| $ \Delta t \equiv t - t_0 $ |
A relação entre ambos é definida como la aceleração centrífuga ($a_c$)
| $ \bar{a} \equiv\displaystyle\frac{ \Delta v }{ \Delta t }$ |
dentro desse intervalo de tempo.
É importante notar que a aceleração média é uma estimativa da aceleração real.
O principal problema é que se a aceleração variar durante o tempo decorrido, o valor da aceleração média pode diferir muito da aceleração média real.
Portanto, a chave é
Determinar a aceleração em um período de tempo suficientemente curto para minimizar a variação.
ID:(3678, 2)
Velocidade com aceleração constante (1)
Equação
Se la aceleração constante ($a_0$), então la aceleração média ($\bar{a}$) é igual ao valor da aceleração, ou seja,
| $ a_0 = \bar{a} $ |
.
Neste caso, la velocidade ($v$) como função de o tempo ($t$) pode ser calculada lembrando que está associada à diferença entre la velocidade ($v$) e la velocidade inicial ($v_0$), bem como o tempo ($t$) e o tempo inicial ($t_0$).
| $ v_1 = v_0 + a_1 ( t_1 - t_0 )$ |
| $ v = v_0 + a_0 ( t - t_0 )$ |
No caso em que la aceleração constante ($a_0$) é igual a la aceleração média ($\bar{a}$), será igual a
| $ a_0 = \bar{a} $ |
.
Portanto, se considerarmos la diferença de velocidade ($\Delta v$) como
| $ \Delta v \equiv v - v_0 $ |
e o tempo decorrido ($\Delta t$) como
| $ \Delta t \equiv t - t_0 $ |
,
temos que a equação para la aceleração constante ($a_0$)
| $ \bar{a} \equiv\displaystyle\frac{ \Delta v }{ \Delta t }$ |
pode ser escrita como
$a_0 = \bar{a} = \displaystyle\frac{\Delta v}{\Delta t} = \displaystyle\frac{v - v_0}{t - t_0}$
portanto, ao rearranjarmos, obtemos
| $ v = v_0 + a_0 ( t - t_0 )$ |
.
Dessa forma, a equação representa uma linha reta no espaço velocidade-tempo.
ID:(3156, 1)
Velocidade com aceleração constante (2)
Equação
Se la aceleração constante ($a_0$), então la aceleração média ($\bar{a}$) é igual ao valor da aceleração, ou seja,
| $ a_0 = \bar{a} $ |
.
Neste caso, la velocidade ($v$) como função de o tempo ($t$) pode ser calculada lembrando que está associada à diferença entre la velocidade ($v$) e la velocidade inicial ($v_0$), bem como o tempo ($t$) e o tempo inicial ($t_0$).
| $ v_2 = v_1 + a_2 ( t_2 - t_1 )$ |
| $ v = v_0 + a_0 ( t - t_0 )$ |
No caso em que la aceleração constante ($a_0$) é igual a la aceleração média ($\bar{a}$), será igual a
| $ a_0 = \bar{a} $ |
.
Portanto, se considerarmos la diferença de velocidade ($\Delta v$) como
| $ \Delta v \equiv v - v_0 $ |
e o tempo decorrido ($\Delta t$) como
| $ \Delta t \equiv t - t_0 $ |
,
temos que a equação para la aceleração constante ($a_0$)
| $ \bar{a} \equiv\displaystyle\frac{ \Delta v }{ \Delta t }$ |
pode ser escrita como
$a_0 = \bar{a} = \displaystyle\frac{\Delta v}{\Delta t} = \displaystyle\frac{v - v_0}{t - t_0}$
portanto, ao rearranjarmos, obtemos
| $ v = v_0 + a_0 ( t - t_0 )$ |
.
Dessa forma, a equação representa uma linha reta no espaço velocidade-tempo.
ID:(3156, 2)
Eu ando com aceleração constante (1)
Equação
No caso de uma aceleração constante ($a_0$), la velocidade ($v$) varia de forma linear com o tempo ($t$), usando la velocidade inicial ($v_0$) e o tempo inicial ($t_0$):
| $ v = v_0 + a_0 ( t - t_0 )$ |
Portanto, podemos calcular a área sob essa reta, o que nos leva a la distância percorrida em um tempo ($\Delta s$), permitindo calcular la posição ($s$) com la velocidade ($s_0$), resultando em:
| $ s_1 = s_0 + v_0 ( t_1 - t_0 )+\displaystyle\frac{1}{2} a_1 ( t_1 - t_0 )^2$ |
| $ s = s_0 + v_0 ( t - t_0 )+\displaystyle\frac{1}{2} a_0 ( t - t_0 )^2$ |
No caso de la aceleração constante ($a_0$), la velocidade ($v$) em função de o tempo ($t$) é uma reta que passa por o tempo inicial ($t_0$) e la velocidade inicial ($v_0$) da forma:
| $ v = v_0 + a_0 ( t - t_0 )$ |
Como la distância percorrida em um tempo ($\Delta s$) é igual à área sob a curva velocidade-tempo, podemos somar a contribuição do retângulo:
$v_0(t-t_0)$
e do triângulo:
$\displaystyle\frac{1}{2}a_0(t-t_0)^2$
Com isso, obtemos com la posição ($s$) e la velocidade ($s_0$):
| $ \Delta s \equiv s - s_0 $ |
Resultando em:
| $ s = s_0 + v_0 ( t - t_0 )+\displaystyle\frac{1}{2} a_0 ( t - t_0 )^2$ |
Isso corresponde à forma geral de uma parábola.
ID:(3157, 1)
Eu ando com aceleração constante (2)
Equação
No caso de uma aceleração constante ($a_0$), la velocidade ($v$) varia de forma linear com o tempo ($t$), usando la velocidade inicial ($v_0$) e o tempo inicial ($t_0$):
| $ v = v_0 + a_0 ( t - t_0 )$ |
Portanto, podemos calcular a área sob essa reta, o que nos leva a la distância percorrida em um tempo ($\Delta s$), permitindo calcular la posição ($s$) com la velocidade ($s_0$), resultando em:
| $ s_2 = s_1 + v_1 ( t_2 - t_1 )+\displaystyle\frac{1}{2} a_2 ( t_2 - t_1 )^2$ |
| $ s = s_0 + v_0 ( t - t_0 )+\displaystyle\frac{1}{2} a_0 ( t - t_0 )^2$ |
No caso de la aceleração constante ($a_0$), la velocidade ($v$) em função de o tempo ($t$) é uma reta que passa por o tempo inicial ($t_0$) e la velocidade inicial ($v_0$) da forma:
| $ v = v_0 + a_0 ( t - t_0 )$ |
Como la distância percorrida em um tempo ($\Delta s$) é igual à área sob a curva velocidade-tempo, podemos somar a contribuição do retângulo:
$v_0(t-t_0)$
e do triângulo:
$\displaystyle\frac{1}{2}a_0(t-t_0)^2$
Com isso, obtemos com la posição ($s$) e la velocidade ($s_0$):
| $ \Delta s \equiv s - s_0 $ |
Resultando em:
| $ s = s_0 + v_0 ( t - t_0 )+\displaystyle\frac{1}{2} a_0 ( t - t_0 )^2$ |
Isso corresponde à forma geral de uma parábola.
ID:(3157, 2)
Caminho de aceleração/frenagem em função da velocidade (1)
Equação
No caso de uma aceleração constante, podemos calcular la posição ($s$) a partir de la velocidade ($s_0$), la velocidade inicial ($v_0$), o tempo ($t$) e o tempo inicial ($t_0$) com a seguinte equação:
| $ s = s_0 + v_0 ( t - t_0 )+\displaystyle\frac{1}{2} a_0 ( t - t_0 )^2$ |
Isso nos permite calcular a relação entre a distância percorrida durante a aceleração/desaceleração em função da mudança de velocidade:
| $ s_1 = s_0 +\displaystyle\frac{ v_1 ^2- v_0 ^2}{2 a_1 }$ |
| $ s = s_0 +\displaystyle\frac{ v ^2- v_0 ^2}{2 a_0 }$ |
Se resolvermos as equações para o tempo ($t$) e o tempo inicial ($t_0$) na equação de la velocidade ($v$), que depende de la velocidade inicial ($v_0$) e la aceleração constante ($a_0$):
| $ v = v_0 + a_0 ( t - t_0 )$ |
obtemos:
$t - t_0= \displaystyle\frac{v - v_0}{a_0}$
Então, substituindo essa expressão na equação de la posição ($s$) com la velocidade ($s_0$):
| $ s = s_0 + v_0 ( t - t_0 )+\displaystyle\frac{1}{2} a_0 ( t - t_0 )^2$ |
obtemos uma expressão do caminho percorrido em função da velocidade:
| $ s = s_0 +\displaystyle\frac{ v ^2- v_0 ^2}{2 a_0 }$ |
ID:(3158, 1)
Caminho de aceleração/frenagem em função da velocidade (2)
Equação
No caso de uma aceleração constante, podemos calcular la posição ($s$) a partir de la velocidade ($s_0$), la velocidade inicial ($v_0$), o tempo ($t$) e o tempo inicial ($t_0$) com a seguinte equação:
| $ s = s_0 + v_0 ( t - t_0 )+\displaystyle\frac{1}{2} a_0 ( t - t_0 )^2$ |
Isso nos permite calcular a relação entre a distância percorrida durante a aceleração/desaceleração em função da mudança de velocidade:
| $ s_2 = s_1 +\displaystyle\frac{ v_2 ^2- v_1 ^2}{2 a_2 }$ |
| $ s = s_0 +\displaystyle\frac{ v ^2- v_0 ^2}{2 a_0 }$ |
Se resolvermos as equações para o tempo ($t$) e o tempo inicial ($t_0$) na equação de la velocidade ($v$), que depende de la velocidade inicial ($v_0$) e la aceleração constante ($a_0$):
| $ v = v_0 + a_0 ( t - t_0 )$ |
obtemos:
$t - t_0= \displaystyle\frac{v - v_0}{a_0}$
Então, substituindo essa expressão na equação de la posição ($s$) com la velocidade ($s_0$):
| $ s = s_0 + v_0 ( t - t_0 )+\displaystyle\frac{1}{2} a_0 ( t - t_0 )^2$ |
obtemos uma expressão do caminho percorrido em função da velocidade:
| $ s = s_0 +\displaystyle\frac{ v ^2- v_0 ^2}{2 a_0 }$ |
ID:(3158, 2)
Distância percorrida (1)
Equação
Podemos calcular la distância percorrida em um tempo ($\Delta s$) a partir de la velocidade ($s_0$) y la posição ($s$) usando a seguinte equação:
| $ \Delta s_1 \equiv s_1 - s_0 $ |
| $ \Delta s \equiv s - s_0 $ |
ID:(4352, 1)
Distância percorrida (2)
Equação
Podemos calcular la distância percorrida em um tempo ($\Delta s$) a partir de la velocidade ($s_0$) y la posição ($s$) usando a seguinte equação:
| $ \Delta s_2 \equiv s_2 - s_1 $ |
| $ \Delta s \equiv s - s_0 $ |
ID:(4352, 2)