Mecanismos
Conceito
Por um lado, é importante diferenciar entre o caso mais simples, unidimensional, e aquele de mais de uma dimensão. Para ambos os casos, a derivada de la velocidade ($v$) em relação a o tempo ($t$), que corresponde à inclinação da curva de la velocidade ($v$), é igual a la aceleração instantânea ($a$). Da mesma forma, a derivada de la velocidade (vector) ($\vec{v}$) em relação a o tempo ($t$), que corresponde a la velocidade (vector) ($\vec{v}$).
Mecanismos
ID:(15398, 0)
Aceleração instantânea
Conceito
A aceleração é definida como a variação da velocidade por tempo. No entanto, esse conceito se resume a uma aceleração média que existe durante o intervalo de tempo considerado.
A limitação da aceleração média é refletida no fato de que um processo que inclui um processo de aceleração seguido por desaceleração até parar terá uma aceleração média de zero. Assim, em média, não haveria aceleração e, se estiver parado, não se moverá, enquanto na verdade avança tanto na fase de aceleração quanto na de frenagem.
Se desejamos conhecer a aceleração em cada instante, devemos considerar um intervalo de tempo suficientemente pequeno para que durante esse tempo a aceleração possa ser considerada aproximadamente constante. Dessa forma, a aceleração média estimada dessa maneira equivale à aceleração existente no momento considerado.
Portanto, falamos em 'aceleração instantânea' para nos referirmos à aceleração em um determinado momento.
ID:(11352, 0)
Aceleração como derivada
Conceito
Se tomarmos o tempo decorrido ($\Delta t$) e observarmos um objeto em movimento com velocidade la velocidade ($v$), e depois observarmos o mesmo objeto em um momento posterior $t+\Delta t$ com velocidade $v(t+\Delta t)$, podemos estimar sua aceleração como a mudança na velocidade durante o tempo decorrido ($\Delta t$):
$a\sim\displaystyle\frac{v(t+\Delta t)-v(t)}{\Delta t}$
À medida que o valor de $\Delta t$ diminui, essa expressão para a aceleração se aproxima da taxa de variação instantânea da velocidade no momento $t$, ou seja, a inclinação da reta tangente à curva de velocidade naquele ponto:

Isso generaliza o conceito de la aceleração instantânea ($a$) para o caso de la aceleração constante ($a_0$), como visto anteriormente, expresso como a derivada de la velocidade ($v$) em relação a o tempo ($t$):
| $ a =\displaystyle\frac{ dv }{ dt }$ |
ID:(11353, 0)
Caminho percorrido como área sob a curva de velocidade
Conceito
Se alguém observa que la velocidade ($v$) é igual a la distância percorrida em um tempo ($\Delta s$) por o tempo decorrido ($\Delta t$), isso indica que o caminho é dado por:
$\Delta s = v\Delta t$
Como o produto $v\Delta t$ representa a área sob a curva de velocidade versus tempo, que também é igual ao caminho percorrido:

Essa área também pode ser calculada com a integral da função correspondente. Portanto, a integral da aceleração entre o tempo inicial ($t_0$) e o tempo ($t$) corresponde à mudança na velocidade entre a velocidade inicial la velocidade inicial ($v_0$) e la velocidade ($v$):
| $ v = v_0 +\displaystyle\int_{t_0}^t a d\tau $ |
ID:(2252, 0)
Curvatura da curva de posição ao longo do tempo
Conceito
La aceleração instantânea ($a$) é igual à derivada de la velocidade ($v$) em relação a o tempo ($t$):
| $ a =\displaystyle\frac{ dv }{ dt }$ |
E já que la velocidade ($v$) é a derivada de la posição ($s$) em relação a o tempo ($t$):
| $ v =\displaystyle\frac{ d s }{ d t }$ |
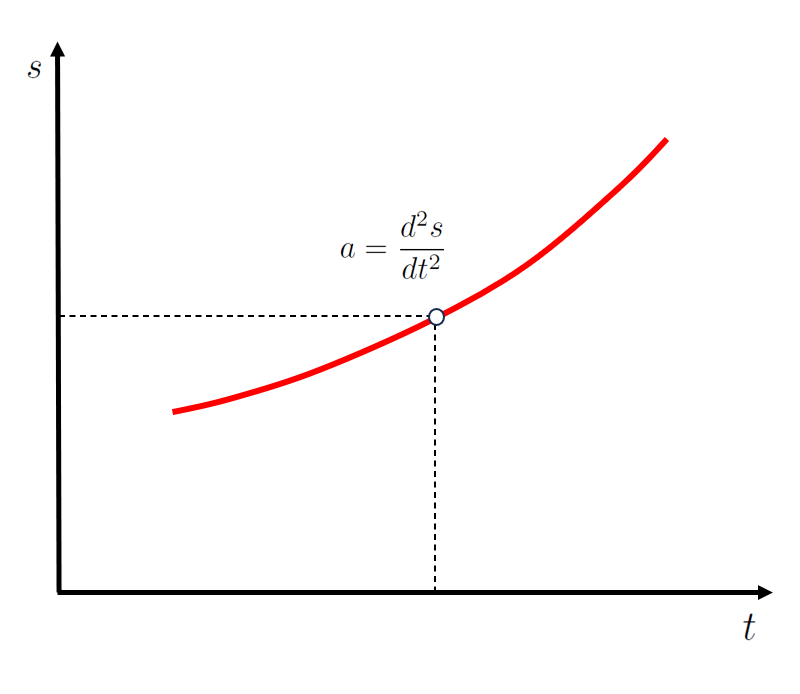
Portanto, la aceleração instantânea ($a$) é a segunda derivada de la posição ($s$) em relação a o tempo ($t$),
| $ a =\displaystyle\frac{ d^2 s }{ d t ^2 }$ |
o que corresponde à curvatura da curva la posição ($s$) em função de o tempo ($t$):
ID:(11354, 0)
Modelo
Conceito
No caso de uma dimensão, la aceleração instantânea ($a$) está relacionada com la velocidade ($v$) através de sua derivada em o tempo ($t$), enquanto a integral de la aceleração instantânea ($a$) no intervalo de o tempo ($t$) a o tempo inicial ($t_0$) fornece la velocidade ($v$) a partir de la velocidade inicial ($v_0$). Em um contexto mais geral, em mais de uma dimensão, a função de la velocidade (vector) ($\vec{v}$) pode ser derivada em o tempo ($t$), resultando em la velocidade (vector) ($\vec{v}$).
Variáveis
Parâmetros
Parâmetro selecionado
Cálculos
Equação
$ \vec{a} = \displaystyle\frac{ d\vec{v} }{ dt }$
&a = @DIF( &v , t , 1)
$ a =\displaystyle\frac{ dv }{ dt }$
a = @DIF( v , t , 1)
$ a =\displaystyle\frac{ d^2 s }{ d t ^2 }$
a = @DIFF( s , t , 2 )
$ v = v_0 +\displaystyle\int_{t_0}^t a d\tau $
v = v_0 + @INT( a, tau, t_0, t )
ID:(15401, 0)
Aceleração instantânea em uma dimensão
Equação
A variável la aceleração média ($\bar{a}$), calculada como a mudança em la diferença de velocidade ($\Delta v$) dividida pelo intervalo de o tempo decorrido ($\Delta t$) através de
| $ \bar{a} \equiv\displaystyle\frac{ \Delta v }{ \Delta t }$ |
é uma aproximação da aceleração real, que tende a distorcer-se quando a aceleração flutua durante o intervalo de tempo. Portanto, introduz-se o conceito de la aceleração instantânea ($a$) determinado em um intervalo de tempo muito pequeno. Neste caso, estamos nos referindo a um intervalo de tempo infinitesimalmente pequeno, e a variação da velocidade ao longo do tempo se reduz à derivada de la velocidade ($v$) em relação a o tempo ($t$):
Se considerarmos a diferença em la velocidade ($v$) nos tempos $t+\Delta t$ e $t$:
$\Delta v = v(t+\Delta t)-v(t)$
e tomarmos $\Delta t$ como o tempo decorrido ($\Delta t$), então, no limite de tempos infinitesimalmente curtos:
$a=\displaystyle\frac{\Delta v}{\Delta t}=\displaystyle\frac{v(t+\Delta t)-v(t)}{\Delta t} \rightarrow \lim_{\Delta t\rightarrow 0}\displaystyle\frac{v(t+\Delta t)-v(t)}{\Delta t}=\displaystyle\frac{dv}{dt}$
Esta última expressão corresponde à derivada da função la velocidade ($v$):
| $ a =\displaystyle\frac{ dv }{ dt }$ |
que, por sua vez, é a inclinação da representação gráfica dessa função em o tempo ($t$).
o que corresponde à derivada da velocidade.
ID:(4356, 0)
Integração de aceleração
Equação
Se la aceleração instantânea ($a$) corresponde à derivada de la velocidade ($v$) em o tempo ($t$),
| $ a =\displaystyle\frac{ dv }{ dt }$ |
então la velocidade ($v$) é igual a la velocidade inicial ($v_0$), e a integração da aceleração de o tempo inicial ($t_0$) a o tempo ($t$) é:
Se integrarmos a definição de la aceleração instantânea ($a$) em o tempo ($t$),
| $ a =\displaystyle\frac{ dv }{ dt }$ |
isso significa que, para um intervalo de tempo $dt$, a distância percorrida é
$dv = a dt$
Se considerarmos $N$ intervalos $dt_i$ com acelerações $a_i$, a variação total na velocidade será
$v - v_0 = \displaystyle\sum_i a_i dt_i$
Se considerarmos a curva de aceleração-tempo, os elementos $a_i dt_i$ correspondem a retângulos com altura $a_i$ e largura $dt_i$. A soma, portanto, corresponde à área sob a curva de aceleração-tempo. Portanto, a soma pode ser expressa como uma integral:
| $ v = v_0 +\displaystyle\int_{t_0}^t a d\tau $ |
ID:(10307, 0)
Aceleração instantânea em função da posição
Equação
Dado que la aceleração instantânea ($a$) representa a inclinação de la velocidade ($v$) em relação a o tempo ($t$),
| $ a =\displaystyle\frac{ dv }{ dt }$ |
e la velocidade ($v$) é, por sua vez, a inclinação de la posição ($s$) em relação a o tempo ($t$),
| $ v =\displaystyle\frac{ d s }{ d t }$ |
podemos expressar la aceleração instantânea ($a$) como a segunda derivada de la posição ($s$) em relação a o tempo ($t$).
Dado que la aceleração instantânea ($a$) é a derivada de la velocidade ($v$) em relação a o tempo ($t$),
| $ a =\displaystyle\frac{ dv }{ dt }$ |
e la velocidade ($v$) é a derivada de la posição ($s$) em relação a o tempo ($t$),
| $ v =\displaystyle\frac{ d s }{ d t }$ |
temos que
$a=\displaystyle\frac{dv}{dt}=\displaystyle\frac{d}{dt}\displaystyle\frac{ds}{dt}=\displaystyle\frac{d^2s}{dt^2}$
portanto,
| $ a =\displaystyle\frac{ d^2 s }{ d t ^2 }$ |
ID:(12572, 0)
Aceleração instantânea em mais dimensões
Equação
Em geral, a velocidade deve ser entendida como um vetor tridimensional. Ou seja, sua la posição ($s$) precisa ser descrita por um vetor uma posição (vector) ($\vec{s}$), para o qual cada componente la velocidade ($v$) pode ser definida conforme mostrado na seguinte equação:
| $ a =\displaystyle\frac{ dv }{ dt }$ |
Isso permite generalizar la velocidade (vector) ($\vec{v}$) da seguinte forma:
Como um vetor pode ser expresso como um conjunto de suas diferentes componentes
$\vec{v}=(v_x,v_y,v_z)$
sua derivada pode ser expressa como a derivada de cada uma de suas componentes
$\displaystyle\frac{d}{dt}\vec{v}=\displaystyle\frac{d}{dt}(v_x,v_y,v_z)=\left(\displaystyle\frac{dv_x}{dt},\displaystyle\frac{dv_y}{dt},\displaystyle\frac{dv_z}{dt}\right)=\displaystyle\frac{d\vec{v}}{dt}=\vec{a}$
em geral, a velocidade instantânea em mais de uma dimensão é
| $ \vec{a} = \displaystyle\frac{ d\vec{v} }{ dt }$ |
ID:(3155, 0)
