mechanisms

Cuando la velocidad angular no es constante, es crucial comprender c mo var a con el tiempo. Para ello, necesitamos conocer la tasa de cambio de la velocidad angular por unidad de tiempo, conocida como aceleraci n angular o desaceleraci n angular, dependiendo de si la velocidad angular est aumentando o disminuyendo.

La aceleraci n angular se determina mediante la medici n de la variaci n de la velocidad angular en relaci n al tiempo.

La aceleraci n angular media se define como la proporci n en la que var a la velocidad angular a lo largo del tiempo. Para medir esta magnitud, es necesario cuantificar c mo cambia la velocidad angular en el transcurso del tiempo.

image

Para llevar a cabo esta medici n de manera precisa, se puede emplear una l mpara estrobosc pica que emite destellos luminosos en intervalos de tiempo definidos. Al capturar una fotograf a en un instante espec fico, es posible determinar la distancia angular que el objeto recorre en ese lapso. Al calcular las velocidades angulares en dos instantes consecutivos, se puede obtener la variaci n de la velocidad angular, y al dividir este cambio entre el intervalo de tiempo entre las fotograf as, se obtiene la aceleraci n angular media.

La ecuaci n que describe esta aceleraci n angular media es la siguiente:

equation=3234

Es importante tener en cuenta que la aceleraci n angular media es una estimaci n de la aceleraci n angular real. Sin embargo, existe un problema fundamental:

Si la aceleraci n angular var a a lo largo del tiempo, el valor de la aceleraci n angular media puede diferir significativamente de la aceleraci n angular promedio.

Por lo tanto, la clave reside en

Determinar la aceleraci n angular en un intervalo de tiempo lo suficientemente corto para minimizar cualquier variaci n significativa.

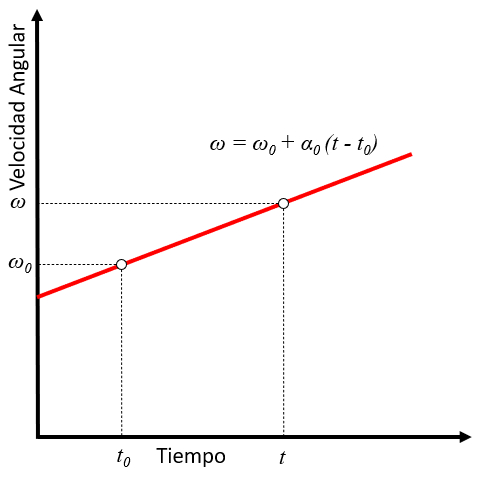
En el caso de una aceleraci n angular constante, la velocidad angular sigue una relaci n lineal en funci n del tiempo:

equation=3237

que se representa en el siguiente gr fico:

image

Con la aceleración constante ($a_0$), la función de la velocidad angular ($\omega$) describe una recta cuya pendiente corresponde a la aceleración angular. Junto con la velocidad angular inicial ($\omega_0$), el tiempo ($t$) y el tiempo inicial ($t_0$), esta relación se expresa mediante la ecuación:

equation=3237

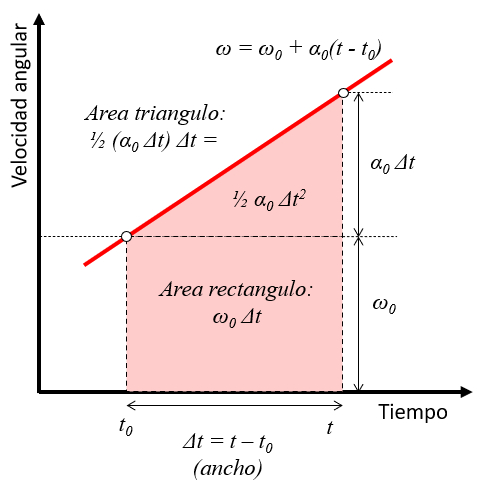
Por lo tanto, el área bajo la curva que representa el desplazamiento angular total se compone de un rectángulo y un triángulo:

image

El rectángulo tiene una altura igual a la velocidad angular inicial y una base correspondiente al tiempo transcurrido. El triángulo tiene una altura que es el producto de la aceleración angular por el tiempo transcurrido, y su base también es igual al tiempo.

Con esta información, se puede calcular el desplazamiento total el ángulo ($\theta$) utilizando el ángulo inicial ($\theta_0$), como se muestra a continuación:

equation=3682

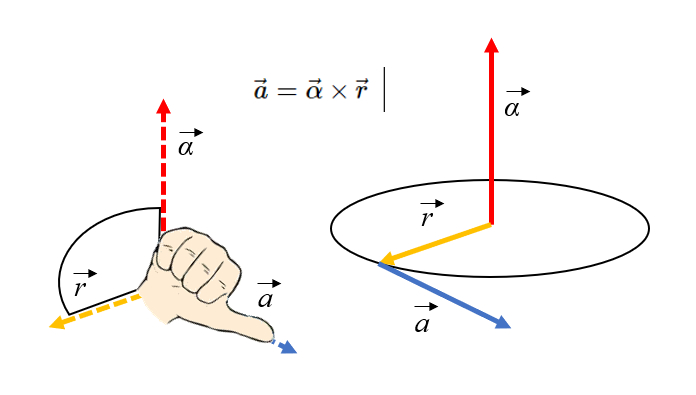
La direcci n de la aceleraci n tangencial puede determinarse utilizando la regla de la mano derecha, donde los dedos se orientan hacia el eje y luego se giran en direcci n al radio:

image

model

La proporci n en la que la variaci n de la velocidad angular a lo largo del tiempo se define como la aceleración angular media ($\bar{\alpha}$). Para medirla, es necesario observar la diferencia de velocidades angulares ($\Delta\omega$) y el tiempo transcurrido ($\Delta t$).

La ecuaci n que describe la aceleración angular media ($\bar{\alpha}$) es la siguiente:

kyon

Para describir la rotaci n de un objeto, es necesario determinar la variación del angulo ($\Delta\theta$). Esto se logra restando el ángulo inicial ($\theta_0$) del valor alcanzado por el objeto durante su rotaci n, que es el ángulo ($\theta$):

kyon

La aceleraci n se define como el cambio en la velocidad angular por unidad de tiempo.

Por lo tanto, la aceleraci n angular la diferencia de velocidades angulares ($\Delta\omega$) se puede expresar en t rminos de la velocidad angular la velocidad angular ($\omega$) y el tiempo la velocidad angular inicial ($\omega_0$) de la siguiente manera:

kyon

Para describir el movimiento de un objeto, debemos calcular el tiempo transcurrido ($\Delta t$). Esta magnitud se obtiene midiendo el tiempo inicial ($t_0$) y el el tiempo ($t$) de dicho movimiento. La duraci n se determina restando el tiempo inicial al tiempo final:

kyon

Con la aceleración angular constante ($\alpha_0$), la velocidad angular ($\omega$) establece una relaci n lineal con el tiempo ($t$), que tambi n incorpora las variables la velocidad angular inicial ($\omega_0$) y el tiempo inicial ($t_0$), tal que:

kyon

Esta ecuaci n representa una recta en el plano de velocidad angular versus tiempo.

Dado que el desplazamiento total corresponde al rea bajo la curva de velocidad angular frente al tiempo, en el caso de una aceleración angular constante ($\alpha_0$), se determina que el desplazamiento el ángulo ($\theta$) con las variables el ángulo inicial ($\theta_0$), el tiempo ($t$), el tiempo inicial ($t_0$) y la velocidad angular inicial ($\omega_0$) es el siguiente:

kyon

Esta expresi n corresponde a la forma general de una par bola.

En el caso de la aceleración angular constante ($\alpha_0$), la funci n de la velocidad angular ($\omega$) respecto a el tiempo ($t$), con variables adicionales la velocidad angular inicial ($\omega_0$) y el tiempo inicial ($t_0$), est expresada por la ecuaci n:

equation=3237

A partir de esta ecuaci n, es posible calcular la relaci n entre el ángulo ($\theta$) y el ángulo inicial ($\theta_0$), as como el cambio en la velocidad angular:

kyon

Si dividimos la relaci n entre la velocidad media ($\bar{v}$), el radio ($r$) y la velocidad angular media ($\bar{\omega}$), expresada en la siguiente ecuaci n:

equation=3233

por el valor de el tiempo transcurrido ($\Delta t$), podemos obtener el factor que nos permite calcular la aceleraci n angular a lo largo de la rbita:

kyon