Konstante Winkelbeschleunigung
Storyboard 
Um eine bestimmte Winkelgeschwindigkeit zu erreichen, muss ein Objekt zunächst seine Winkelgeschwindigkeit von Ruhe aus erhöhen. Dieser Vorgang wird als Winkelbeschleunigung bezeichnet und wird in Bezug auf die Änderung der Winkelgeschwindigkeit im Laufe der Zeit definiert. Andererseits, wenn das Ziel darin besteht, die Winkelgeschwindigkeit zu verringern und sogar die Rotation des Objekts zu stoppen, wird auch eine Winkelbeschleunigung eingeführt, jedoch mit dem entgegengesetzten Vorzeichen zur Winkelgeschwindigkeit (wenn die Winkelgeschwindigkeit positiv ist, ist die Winkelbeschleunigung negativ, und umgekehrt), was als Bremsen der Rotation bekannt ist.
ID:(612, 0)
Konstante Winkelbeschleunigung
Storyboard 
Um eine bestimmte Winkelgeschwindigkeit zu erreichen, muss ein Objekt zunächst seine Winkelgeschwindigkeit von Ruhe aus erhöhen. Dieser Vorgang wird als Winkelbeschleunigung bezeichnet und wird in Bezug auf die Änderung der Winkelgeschwindigkeit im Laufe der Zeit definiert. Andererseits, wenn das Ziel darin besteht, die Winkelgeschwindigkeit zu verringern und sogar die Rotation des Objekts zu stoppen, wird auch eine Winkelbeschleunigung eingeführt, jedoch mit dem entgegengesetzten Vorzeichen zur Winkelgeschwindigkeit (wenn die Winkelgeschwindigkeit positiv ist, ist die Winkelbeschleunigung negativ, und umgekehrt), was als Bremsen der Rotation bekannt ist.
Variablen
Berechnungen
Berechnungen
Gleichungen
Die Definition der durchschnittlichen Winkelbeschleunigung basiert auf dem zur ckgelegten Winkel
und der verstrichenen Zeit
Die Beziehung zwischen beiden wird als die durchschnittliche Winkelbeschleunigung definiert
innerhalb dieses Zeitintervalls.
Angesichts dessen, dass die Mittlere Beschleunigung ($\bar{a}$) gleich die Geschwindigkeit Unterschied ($\Delta v$) und der Abgelaufene Zeit ($\Delta t$) gem
und die Mittlere Winkelbeschleunigung ($\bar{\alpha}$) gleich die Unterschied in der Winkelgeschwindigkeiten ($\Delta\omega$) und der Abgelaufene Zeit ($\Delta t$) laut
ist, folgt daraus, dass
$\bar{a}=\displaystyle\frac{\Delta v}{\Delta t}=r\displaystyle\frac{\Delta\omega}{\Delta t}=\bar{\alpha}$
Unter der Annahme, dass die Mittlere Winkelbeschleunigung ($\bar{\alpha}$) gleich die Constant Angular Acceleration ($\alpha_0$) ist
und angenommen, dass die Mittlere Beschleunigung ($\bar{a}$) gleich die konstante Beschleunigung ($a_0$) ist
ergibt sich folgende Gleichung:
Wenn wir annehmen, dass die Mittlere Winkelbeschleunigung ($\bar{\alpha}$) konstant und gleich die Constant Angular Acceleration ($\alpha_0$) ist, dann gilt die folgende Gleichung:
Daher, unter Ber cksichtigung von die Unterschied in der Winkelgeschwindigkeiten ($\Delta\omega$) zusammen mit die Winkelgeschwindigkeit ($\omega$) und die Anfängliche Winkelgeschwindigkeit ($\omega_0$):
und der Abgelaufene Zeit ($\Delta t$) in Bezug auf der Zeit ($t$) und der Startzeit ($t_0$):
kann die Gleichung f r die Mittlere Winkelbeschleunigung ($\bar{\alpha}$):
wie folgt ausgedr ckt werden:
$\alpha_0 = \alpha = \displaystyle\frac{\Delta \omega}{\Delta t} = \displaystyle\frac{\omega - \omega_0}{t - t_0}$
Durch Aufl sen erhalten wir:
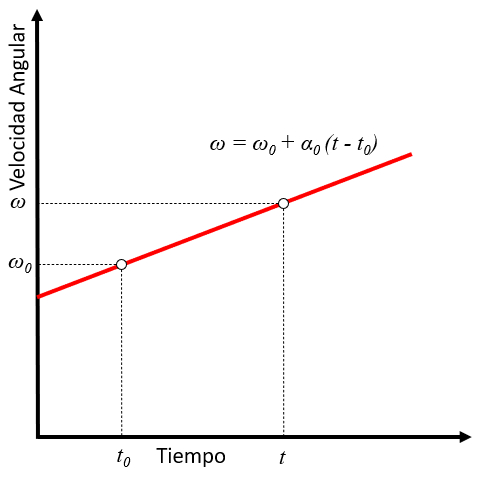
Im Fall von die Constant Angular Acceleration ($\alpha_0$) folgt die Winkelgeschwindigkeit ($\omega$) als Funktion von der Zeit ($t$) einer linearen Beziehung mit der Startzeit ($t_0$) und die Anfängliche Winkelgeschwindigkeit ($\omega_0$) in der Form:
Da der zur ckgelegte Winkel gleich der Fl che unter der Kurve der Winkelgeschwindigkeit-Zeit ist, kann in diesem Fall der Beitrag des Rechtecks:
$\omega_0(t-t_0)$
und des Dreiecks:
$\displaystyle\frac{1}{2}\alpha_0(t-t_0)^2$
hinzugef gt werden.
Dies f hrt uns zu dem Ausdruck f r der Winkel ($\theta$) und der Anfangswinkel ($\theta_0$):
Wenn wir die Zeit in der Gleichung von die Winkelgeschwindigkeit ($\omega$) aufl sen, die die Variablen die Anfängliche Winkelgeschwindigkeit ($\omega_0$), der Zeit ($t$), der Startzeit ($t_0$) und die Constant Angular Acceleration ($\alpha_0$) umfasst:
erhalten wir den folgenden Ausdruck f r die Zeit:
$t - t_0 = \displaystyle\frac{\omega - \omega_0}{\alpha_0}$
Diese L sung kann in die Gleichung eingesetzt werden, um der Winkel ($\theta$) unter Verwendung von der Anfangswinkel ($\theta_0$) wie folgt zu berechnen:
was in der folgenden Gleichung resultiert:
Beispiele
Wenn die Winkelgeschwindigkeit nicht konstant ist, ist es wichtig zu verstehen, wie sie sich im Laufe der Zeit ndert. Hierf r m ssen wir die nderungsrate der Winkelgeschwindigkeit pro Zeiteinheit kennen, die als Winkelbeschleunigung oder -verz gerung bezeichnet wird, je nachdem, ob die Winkelgeschwindigkeit zunimmt oder abnimmt.
Die Winkelbeschleunigung wird durch Messung der Variation der Winkelgeschwindigkeit ber die Zeit bestimmt.
Die durchschnittliche Winkelbeschleunigung wird als das Verh ltnis definiert, in dem sich die Winkelgeschwindigkeit im Laufe der Zeit ndert. Um diese Gr e genau zu messen, ist es erforderlich, zu quantifizieren, wie sich die Winkelgeschwindigkeit im Laufe der Zeit ndert.
Die Gleichung, die diese durchschnittliche Winkelbeschleunigung beschreibt, lautet wie folgt:
Es ist wichtig zu beachten, dass die durchschnittliche Winkelbeschleunigung eine Sch tzung der tats chlichen Winkelbeschleunigung ist. Es gibt jedoch ein grundlegendes Problem:
Wenn die Winkelbeschleunigung im Laufe der Zeit variiert, kann der Wert der durchschnittlichen Winkelbeschleunigung erheblich von der durchschnittlichen Winkelbeschleunigung abweichen.
Daher liegt der Schl ssel darin,
Die Winkelbeschleunigung innerhalb eines ausreichend kurzen Zeitintervalls zu bestimmen, um jegliche signifikante Variation zu minimieren.
Im Fall einer konstanten Winkelbeschleunigung folgt die Winkelgeschwindigkeit einer linearen Beziehung zur Zeit:
wie in der folgenden Grafik dargestellt:
Mit die konstante Beschleunigung ($a_0$) beschreibt die Funktion von die Winkelgeschwindigkeit ($\omega$) eine Gerade, deren Steigung der Winkelbeschleunigung entspricht. Zusammen mit die Anfängliche Winkelgeschwindigkeit ($\omega_0$), der Zeit ($t$) und der Startzeit ($t_0$) wird diese Beziehung durch die folgende Gleichung ausgedrückt:
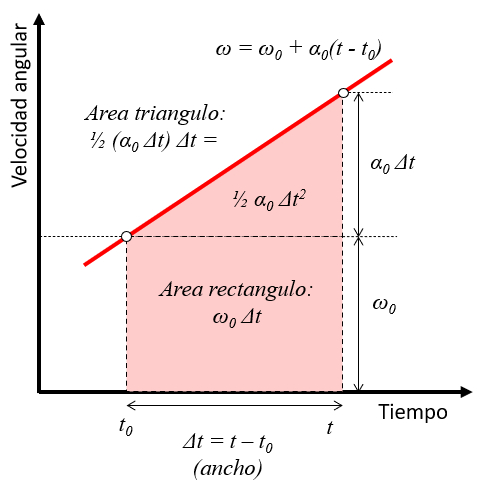
Die Fläche unter der Kurve die die gesamte Winkelverschiebung darstellt setzt sich daher aus einem Rechteck und einem Dreieck zusammen:
Das Rechteck hat eine Höhe, die der anfänglichen Winkelgeschwindigkeit entspricht, und eine Basis, die der verstrichenen Zeit entspricht. Das Dreieck hat eine Höhe, die dem Produkt aus Winkelbeschleunigung und verstrichener Zeit entspricht, und ebenfalls eine Basis, die gleich der Zeit ist.
Mit diesen Informationen kann die Gesamtverschiebung der Winkel ($\theta$) unter Verwendung von der Anfangswinkel ($\theta_0$) wie folgt berechnet werden:
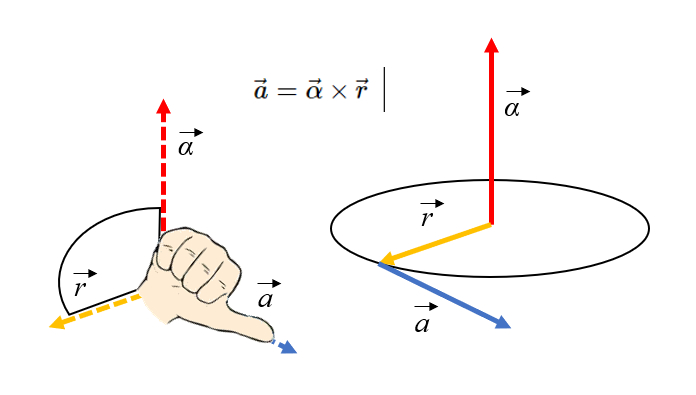
Die Ausrichtung der Tangentialbeschleunigung kann mithilfe der Rechten-Hand-Regel ermittelt werden, indem die Finger in Richtung der Achse zeigen und dann in Richtung des Radius gedreht werden:
Die Rate, mit der sich die Winkelgeschwindigkeit im Laufe der Zeit ndert, wird als die Mittlere Winkelbeschleunigung ($\bar{\alpha}$) definiert. Um dies zu messen, m ssen wir die Unterschied in der Winkelgeschwindigkeiten ($\Delta\omega$) und der Abgelaufene Zeit ($\Delta t$) beobachten.
Die Gleichung, die die Mittlere Winkelbeschleunigung ($\bar{\alpha}$) beschreibt, lautet wie folgt:
Um die Rotation eines Objekts zu beschreiben, m ssen wir die Winkelvariation ($\Delta\theta$) bestimmen. Dies geschieht, indem wir der Anfangswinkel ($\theta_0$) von der Winkel ($\theta$) subtrahieren, den Wert, den das Objekt w hrend seiner Rotation erreicht:
Die Beschleunigung wird als nderung der Winkelgeschwindigkeit pro Zeiteinheit definiert.
Daher kann die Winkelbeschleunigung die Unterschied in der Winkelgeschwindigkeiten ($\Delta\omega$) in Bezug auf die Winkelgeschwindigkeit die Winkelgeschwindigkeit ($\omega$) und die Zeit die Anfängliche Winkelgeschwindigkeit ($\omega_0$) wie folgt ausgedr ckt werden:
Um die Bewegung eines Objekts zu beschreiben, m ssen wir der Abgelaufene Zeit ($\Delta t$) berechnen. Diese Gr e wird durch Messung von der Startzeit ($t_0$) und der der Zeit ($t$) dieser Bewegung erhalten. Die Dauer wird bestimmt, indem die Anfangszeit von der Endzeit subtrahiert wird:
Mit die Constant Angular Acceleration ($\alpha_0$) stellt die Winkelgeschwindigkeit ($\omega$) eine lineare Beziehung mit der Zeit ($t$) her, die auch die Variablen die Anfängliche Winkelgeschwindigkeit ($\omega_0$) und der Startzeit ($t_0$) einbezieht, wie folgt:
Diese Gleichung repr sentiert eine Gerade im Raum der Winkelgeschwindigkeit gegen ber der Zeit.
Da der gesamte Weg der Fl che unter der Kurve der Winkelgeschwindigkeit gegen ber der Zeit entspricht, ergibt sich im Fall von eine Constant Angular Acceleration ($\alpha_0$), dass der Weg der Winkel ($\theta$) mit den Variablen der Anfangswinkel ($\theta_0$), der Zeit ($t$), der Startzeit ($t_0$) und die Anfängliche Winkelgeschwindigkeit ($\omega_0$) wie folgt ist:
Diese Ausdruck entspricht der allgemeinen Form einer Parabel.
Im Fall von die Constant Angular Acceleration ($\alpha_0$) wird die Funktion von die Winkelgeschwindigkeit ($\omega$) bez glich der Zeit ($t$), zusammen mit den zus tzlichen Variablen die Anfängliche Winkelgeschwindigkeit ($\omega_0$) und der Startzeit ($t_0$), durch die Gleichung ausgedr ckt:
Aus dieser Gleichung l sst sich die Beziehung zwischen der Winkel ($\theta$) und der Anfangswinkel ($\theta_0$) sowie die Ver nderung der Winkelgeschwindigkeit berechnen:
Wenn wir das Verh ltnis zwischen die Mittlere Geschwindigkeit ($\bar{v}$), der Radio ($r$) und die Mittlere Winkelgeschwindigkeit ($\bar{\omega}$), das in der folgenden Gleichung dargestellt ist:
durch den Wert von der Abgelaufene Zeit ($\Delta t$) teilen, k nnen wir den Faktor ermitteln, der es uns erm glicht, die Winkelbeschleunigung entlang der Umlaufbahn zu berechnen:
ID:(612, 0)