Interceptar a velocidad angular constante
Storyboard 
Los objetos pueden intersectarse cuando coinciden en ángulo en un mismo momento. Para lograrlo, deben desplazarse desde sus respectivos ángulos iniciales con velocidades angulares que les permitan coincidir en ángulo y tiempo al final del recorrido.
ID:(1450, 0)
Interceptar a velocidad angular constante
Storyboard 
Los objetos pueden intersectarse cuando coinciden en ángulo en un mismo momento. Para lograrlo, deben desplazarse desde sus respectivos ángulos iniciales con velocidades angulares que les permitan coincidir en ángulo y tiempo al final del recorrido.
Variables
Cálculos
Cálculos
Ecuaciones
En el caso de que la velocidad angular inicial ($\omega_0$) sea igual a la velocidad angular media ($\bar{\omega}$),
Por lo tanto, con la diferencia de ángulos ($\Delta\theta$), que es igual a el ángulo ($\theta$) dividido por el ángulo inicial ($\theta_0$), obtenemos:
Y con el tiempo transcurrido ($\Delta t$), que es igual a el tiempo ($t$) dividido por el tiempo inicial ($t_0$), obtenemos:
Podemos reescribir la ecuaci n de la velocidad angular media ($\bar{\omega}$) como:
Esto se puede expresar como:
$\omega_0 = \omega = \displaystyle\frac{\Delta\theta}{\Delta t} = \displaystyle\frac{\theta - \theta_0}{t - t_0}$
Despejando, obtenemos:
En el caso de que la velocidad angular inicial ($\omega_0$) sea igual a la velocidad angular media ($\bar{\omega}$),
Por lo tanto, con la diferencia de ángulos ($\Delta\theta$), que es igual a el ángulo ($\theta$) dividido por el ángulo inicial ($\theta_0$), obtenemos:
Y con el tiempo transcurrido ($\Delta t$), que es igual a el tiempo ($t$) dividido por el tiempo inicial ($t_0$), obtenemos:
Podemos reescribir la ecuaci n de la velocidad angular media ($\bar{\omega}$) como:
Esto se puede expresar como:
$\omega_0 = \omega = \displaystyle\frac{\Delta\theta}{\Delta t} = \displaystyle\frac{\theta - \theta_0}{t - t_0}$
Despejando, obtenemos:
Como la velocidad media ($\bar{v}$) es con la distancia recorrida en un tiempo ($\Delta s$) y el tiempo transcurrido ($\Delta t$), igual a
y con la distancia recorrida en un tiempo ($\Delta s$) expresado como arco de un c rculo, y el radio ($r$) y la variación del angulo ($\Delta\theta$) son
y la definici n de la velocidad angular media ($\bar{\omega}$) es
entonces,
$v=\displaystyle\frac{\Delta s}{\Delta t}=r\displaystyle\frac{\Delta\theta}{\Delta t}=r\omega$
Como la relaci n es general, se puede aplicar para valores instant neos, lo que resulta en
Como la velocidad media ($\bar{v}$) es con la distancia recorrida en un tiempo ($\Delta s$) y el tiempo transcurrido ($\Delta t$), igual a
y con la distancia recorrida en un tiempo ($\Delta s$) expresado como arco de un c rculo, y el radio ($r$) y la variación del angulo ($\Delta\theta$) son
y la definici n de la velocidad angular media ($\bar{\omega}$) es
entonces,
$v=\displaystyle\frac{\Delta s}{\Delta t}=r\displaystyle\frac{\Delta\theta}{\Delta t}=r\omega$
Como la relaci n es general, se puede aplicar para valores instant neos, lo que resulta en
La definici n de la velocidad angular media ($\bar{\omega}$) se considera la variación del angulo ($\Delta\theta$),
y el tiempo transcurrido ($\Delta t$),
La relaci n entre ambos se define como la velocidad angular media ($\bar{\omega}$):
La definici n de la velocidad angular media ($\bar{\omega}$) se considera la variación del angulo ($\Delta\theta$),
y el tiempo transcurrido ($\Delta t$),
La relaci n entre ambos se define como la velocidad angular media ($\bar{\omega}$):
Ejemplos
En el caso de una intersecci n, se trata de dos cuerpos que se desplazan de tal manera que coincidir n en ERROR:10307,0 en el tiempo un tiempo de intersección ($t$).
Para lograr esto, cada cuerpo:
• Comienza su desplazamiento en el tiempo inicial del primer objeto ($t_1$) en el ángulo inicial del primer cuerpo ($\theta_1$) con una velocidad angular del cuerpo 1 ($\omega_1$).
• Comienza su desplazamiento en el tiempo inicial del segundo objeto ($t_2$) en el ángulo inicial del segundo cuerpo ($\theta_2$) con una velocidad angular del cuerpo 2 ($\omega_2$).
Estas condiciones deben cumplirse para lograr la intersecci n.
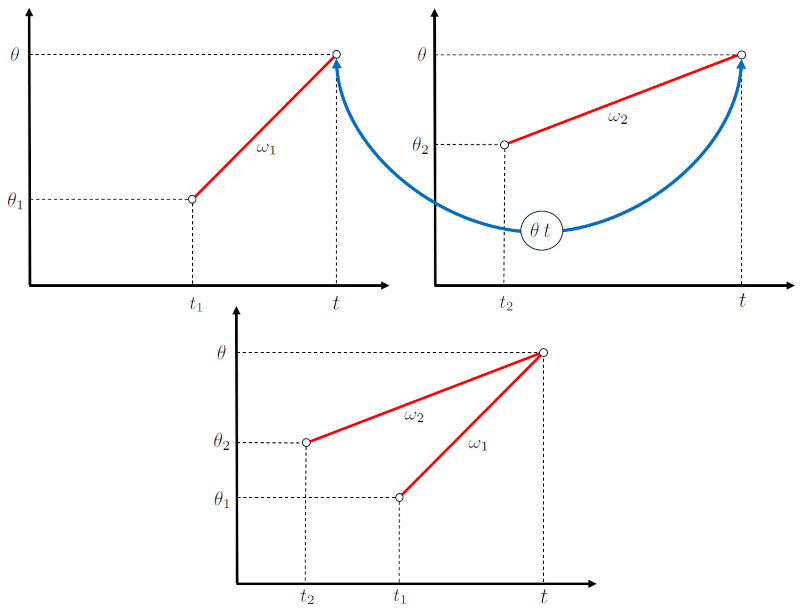
Con ello, los diagramas del ngulo en el tiempo pueden ser acoplados como se muestra en la siguiente representaci n:
En el caso de una intersecci n o choque entre dos objetos, es com n que la velocidad angular del cuerpo 1 ($\omega_1$) y la velocidad angular del cuerpo 2 ($\omega_2$) deban estar configurados de manera que se produzca la coincidencia.
Esto implica que el ángulo recorrido por el primer cuerpo ($\Delta\theta_1$) y la duración del viaje del primer objeto ($\Delta t_1$) deben resultar en una velocidad angular del cuerpo 1 ($\omega_1$),
de manera que, con el ángulo recorrido por el segundo cuerpo ($\Delta\theta_2$) y la duración de viaje del segundo objeto ($\Delta t_2$), se obtenga una velocidad angular del cuerpo 2 ($\omega_2$),
para que finalmente coincidan en tiempo y espacio (posici n):
En el caso de un movimiento en el que dos objetos se interceptan, como la ángulo de la intersección ($\theta$) y el tiempo de intersección ($t$), es com n para ambos. Por lo tanto, si para el primer objeto, el tiempo inicial del primer objeto ($t_1$) y el ángulo inicial del primer cuerpo ($\theta_1$) con la velocidad angular del cuerpo 1 ($\omega_1$) cumplen:
y para el segundo objeto, el tiempo inicial del segundo objeto ($t_2$) y el ángulo inicial del segundo cuerpo ($\theta_2$) con la velocidad angular del cuerpo 2 ($\omega_2$) se cumplen:
Esto se representa como:
Para describir la rotaci n de un objeto, es necesario determinar la variación del angulo ($\Delta\theta$). Esto se logra restando el ángulo inicial ($\theta_0$) del valor alcanzado por el objeto durante su rotaci n, que es el ángulo ($\theta$):
Para describir la rotaci n de un objeto, es necesario determinar la variación del angulo ($\Delta\theta$). Esto se logra restando el ángulo inicial ($\theta_0$) del valor alcanzado por el objeto durante su rotaci n, que es el ángulo ($\theta$):
Para describir el movimiento de un objeto, debemos calcular el tiempo transcurrido ($\Delta t$). Esta magnitud se obtiene midiendo el tiempo inicial ($t_0$) y el el tiempo ($t$) de dicho movimiento. La duraci n se determina restando el tiempo inicial al tiempo final:
Para describir el movimiento de un objeto, debemos calcular el tiempo transcurrido ($\Delta t$). Esta magnitud se obtiene midiendo el tiempo inicial ($t_0$) y el el tiempo ($t$) de dicho movimiento. La duraci n se determina restando el tiempo inicial al tiempo final:
En el caso de que la velocidad angular sea constante, la velocidad angular media ($\bar{\omega}$) coincide con el valor de la velocidad angular inicial ($\omega_0$), por lo que
En este caso, podemos calcular el ngulo recorrido en funci n del tiempo recordando que este se asocia a la diferencia entre el ngulo actual y el inicial, as como el tiempo actual y el inicial. Por lo tanto, el ángulo ($\theta$) es igual a el ángulo inicial ($\theta_0$), la velocidad angular inicial ($\omega_0$), el tiempo ($t$) y el tiempo inicial ($t_0$) como se muestra a continuaci n:
La ecuaci n representa una recta en el espacio ngulo-tiempo.
En el caso de que la velocidad angular sea constante, la velocidad angular media ($\bar{\omega}$) coincide con el valor de la velocidad angular inicial ($\omega_0$), por lo que
En este caso, podemos calcular el ngulo recorrido en funci n del tiempo recordando que este se asocia a la diferencia entre el ngulo actual y el inicial, as como el tiempo actual y el inicial. Por lo tanto, el ángulo ($\theta$) es igual a el ángulo inicial ($\theta_0$), la velocidad angular inicial ($\omega_0$), el tiempo ($t$) y el tiempo inicial ($t_0$) como se muestra a continuaci n:
La ecuaci n representa una recta en el espacio ngulo-tiempo.
Para estimar el desplazamiento de un objeto, es necesario conocer su la velocidad angular ($\omega$) en funci n de el tiempo ($t$). Por lo tanto, se introduce la la velocidad angular media ($\bar{\omega}$), definida como la proporci n entre la variación del angulo ($\Delta\theta$) y el tiempo transcurrido ($\Delta t$).
Para medir esto, se puede utilizar un sistema como el que se muestra en la imagen:
Para determinar la velocidad angular media, se coloca un elemento reflectante en el eje o en un disco con varios elementos reflectantes, y se registra el paso para estimar la longitud del arco $\Delta s$ y el ngulo asociado con el radio $r$. Luego se registra la diferencia de tiempo cuando la marca pasa frente al sensor como $\Delta t$. La velocidad angular media se determina dividiendo el ngulo recorrido por el tiempo transcurrido.
La ecuaci n que describe la velocidad angular media es:
Cabe destacar que la velocidad media es una estimaci n de la velocidad angular real. El problema principal es que:
Si la velocidad angular var a durante el tiempo transcurrido, el valor de la velocidad angular media puede ser muy diferente de la velocidad angular promedio.
Por lo tanto, la clave es:
Determinar la velocidad en un tiempo transcurrido suficientemente corto para minimizar su variaci n.
Para estimar el desplazamiento de un objeto, es necesario conocer su la velocidad angular ($\omega$) en funci n de el tiempo ($t$). Por lo tanto, se introduce la la velocidad angular media ($\bar{\omega}$), definida como la proporci n entre la variación del angulo ($\Delta\theta$) y el tiempo transcurrido ($\Delta t$).
Para medir esto, se puede utilizar un sistema como el que se muestra en la imagen:
Para determinar la velocidad angular media, se coloca un elemento reflectante en el eje o en un disco con varios elementos reflectantes, y se registra el paso para estimar la longitud del arco $\Delta s$ y el ngulo asociado con el radio $r$. Luego se registra la diferencia de tiempo cuando la marca pasa frente al sensor como $\Delta t$. La velocidad angular media se determina dividiendo el ngulo recorrido por el tiempo transcurrido.
La ecuaci n que describe la velocidad angular media es:
Cabe destacar que la velocidad media es una estimaci n de la velocidad angular real. El problema principal es que:
Si la velocidad angular var a durante el tiempo transcurrido, el valor de la velocidad angular media puede ser muy diferente de la velocidad angular promedio.
Por lo tanto, la clave es:
Determinar la velocidad en un tiempo transcurrido suficientemente corto para minimizar su variaci n.
Si dividimos la relaci n entre la distancia recorrida en un tiempo ($\Delta s$) y el radio ($r$) por la variación del angulo ($\Delta\theta$),
y luego dividimos eso por el tiempo transcurrido ($\Delta t$), obtenemos la relaci n que nos permite calcular la velocidad ($v$) a lo largo de la rbita, conocida como velocidad tangencial, que es igual a la velocidad angular ($\omega$):
Si dividimos la relaci n entre la distancia recorrida en un tiempo ($\Delta s$) y el radio ($r$) por la variación del angulo ($\Delta\theta$),
y luego dividimos eso por el tiempo transcurrido ($\Delta t$), obtenemos la relaci n que nos permite calcular la velocidad ($v$) a lo largo de la rbita, conocida como velocidad tangencial, que es igual a la velocidad angular ($\omega$):
ID:(1450, 0)