Aceleración centrifuga y centripeta
Storyboard 
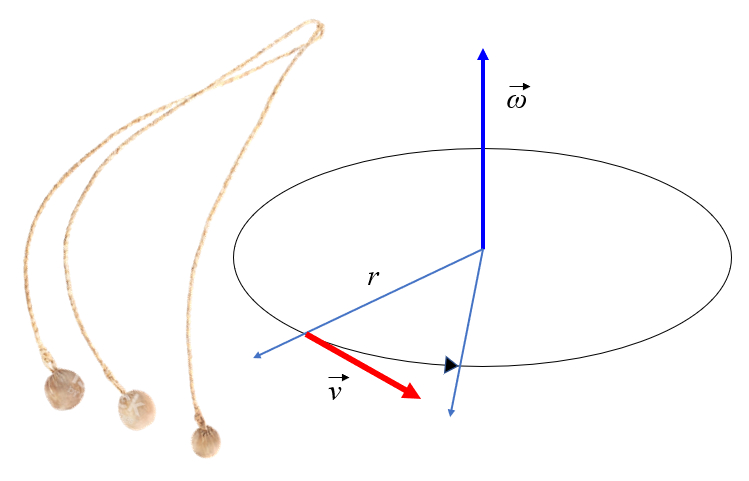
Todo objeto con velocidad tiende a desplazarse en línea recta. Para que un objeto pueda seguir una órbita circular, necesita "caer" radicalmente desde su trayectoria rectilínea hasta el radio de la órbita. Esta "caída" corresponde a una aceleración centrípeta, que es hacia el centro y es lo que percibiría un observador externo al sistema.
Por otro lado, si el objeto continúa en su trayectoria rectilínea en lugar de seguir la órbita circular, un observador dentro del sistema en rotación percibirá una aceleración similar, pero alejándose del centro, lo que se conoce como aceleración centrífuga (centri = centro, fuga = alejándose).
ID:(758, 0)
Aceleración centrifuga y centripeta
Storyboard 
Todo objeto con velocidad tiende a desplazarse en línea recta. Para que un objeto pueda seguir una órbita circular, necesita "caer" radicalmente desde su trayectoria rectilínea hasta el radio de la órbita. Esta "caída" corresponde a una aceleración centrípeta, que es hacia el centro y es lo que percibiría un observador externo al sistema. Por otro lado, si el objeto continúa en su trayectoria rectilínea en lugar de seguir la órbita circular, un observador dentro del sistema en rotación percibirá una aceleración similar, pero alejándose del centro, lo que se conoce como aceleración centrífuga (centri = centro, fuga = alejándose).
Variables
Cálculos
Cálculos
Ecuaciones
En el caso de que la velocidad angular inicial ($\omega_0$) sea igual a la velocidad angular media ($\bar{\omega}$),
Por lo tanto, con la diferencia de ángulos ($\Delta\theta$), que es igual a el ángulo ($\theta$) dividido por el ángulo inicial ($\theta_0$), obtenemos:
Y con el tiempo transcurrido ($\Delta t$), que es igual a el tiempo ($t$) dividido por el tiempo inicial ($t_0$), obtenemos:
Podemos reescribir la ecuaci n de la velocidad angular media ($\bar{\omega}$) como:
Esto se puede expresar como:
$\omega_0 = \omega = \displaystyle\frac{\Delta\theta}{\Delta t} = \displaystyle\frac{\theta - \theta_0}{t - t_0}$
Despejando, obtenemos:
Con la distancia recorrida en un tiempo ($\Delta s$) es con la posición ($s$) y la posición inicial ($s_0$):
y el tiempo transcurrido ($\Delta t$) es con el tiempo ($t$) y el tiempo inicial ($t_0$):
Se tiene que la ecuaci n de la velocidad media:
puede escribirse como:
$v_0 = \bar{v} = \displaystyle\frac{\Delta s}{\Delta t} = \displaystyle\frac{s - s_0}{t - t_0}$
Por lo tanto, despejando, se obtiene:
Como la velocidad media ($\bar{v}$) es con la distancia recorrida en un tiempo ($\Delta s$) y el tiempo transcurrido ($\Delta t$), igual a
y con la distancia recorrida en un tiempo ($\Delta s$) expresado como arco de un c rculo, y el radio ($r$) y la variación del angulo ($\Delta\theta$) son
y la definici n de la velocidad angular media ($\bar{\omega}$) es
entonces,
$v=\displaystyle\frac{\Delta s}{\Delta t}=r\displaystyle\frac{\Delta\theta}{\Delta t}=r\omega$
Como la relaci n es general, se puede aplicar para valores instant neos, lo que resulta en
La definici n de la velocidad angular media ($\bar{\omega}$) se considera la variación del angulo ($\Delta\theta$),
y el tiempo transcurrido ($\Delta t$),
La relaci n entre ambos se define como la velocidad angular media ($\bar{\omega}$):
Al ser la aceleraci n centr fuga igual a
con
podemos concluir que:
Si la distancia recorrida es peque a ($v\Delta t\ll r$), la ra z cuadrada de la distancia entre el centro y el cuerpo,
$\sqrt{r^2+(v\Delta t)^2}$
puede aproximarse como
$r+\displaystyle\frac{1}{2}\displaystyle\frac{v^2}{r}\Delta t^2$
lo cual corresponde a una par bola en funci n del tiempo $\Delta t$. Por lo tanto, el comportamiento puede describirse con una aceleraci n igual a:
Ejemplos
Si un objeto se somete a un modo de mantener un radio constante, girar como se indica en la figura. Al observar la figura, se notar que la masa realiza un movimiento de traslaci n con una velocidad tangencial que es igual al radio por la velocidad angular:
Sin embargo, si se corta el elemento que une el objeto al eje, este continuar movi ndose tangencialmente en l nea recta.
Si un cuerpo atado a una cuerda de longitud $r$ gira con una velocidad tangencial $v$ y la cuerda es cortada, el cuerpo continuar movi ndose inercialmente en l nea recta con velocidad constante $v$.
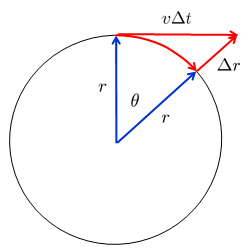
En un intervalo de tiempo $\Delta t$, el cuerpo habr recorrido la distancia $v\Delta t$ tangencialmente a su rbita anterior. Desde el punto de vista de un observador en el eje del sistema de rotaci n, la distancia se calcula utilizando el teorema de Pit goras, sumando el cuadrado del radio de la rbita con el cuadrado de la distancia recorrida:
$\sqrt{r^2+v^2\Delta t^2}$
Si estudiamos una catapulta, notaremos que la bala primero se mueve a lo largo de la curva que describe la cuchara. Esto sucede porque la cuchara est dise ada para retener la bala. Una vez que se detiene el brazo, la bala contin a en l nea recta en forma tangencial al c rculo que recorr a.
Si un cuerpo no est retenido y viaja con una velocidad tangencial $v$, recorrer en un tiempo $\Delta t$ la distancia $v\Delta t$, viajando desde el punto B hasta el punto C. Sin embargo, si contin a orbitando, despu s del tiempo $\Delta t$ llegar al punto D. Si el objeto llega al punto C, desde la perspectiva de un observador en la Tierra, existir una aceleraci n que hace que el objeto se aleje de la Tierra (aceleraci n centr fuga), recorriendo en el tiempo $\Delta t$ la distancia $\Delta r$.
Para un observador en el espacio, un objeto en rbita se encuentra en una ca da constante: en lugar de terminar en el punto C, cae en el tiempo $\Delta t$ la distancia $\Delta r$ hasta llegar al punto D. En ambos casos, podemos representar la situaci n y utilizando el teorema de Pit goras, podemos ver que se debe cumplir la siguiente ecuaci n:
$(r+\Delta r)^2=r^2+(v\Delta t)^2$
Si desarrollamos el cuadrado de la ecuaci n, se reduce a:
$2\Delta rr+\Delta r^2=v^2\Delta t^2$
Como la variaci n del radio $\Delta r$ es mucho m s peque a que el radio en s ($r\ll\Delta r$), podemos concluir que:
$2\Delta rr=v^2\Delta t^2$
o despejando $\Delta r$:
$\Delta r=\displaystyle\frac{1}{2}\displaystyle\frac{v^2}{r}\Delta t^2$
Comparando esta ecuaci n con la ecuaci n $s=at^2/2$, se concluye que el cuerpo acelera con una aceleraci n igual a $v^2/r$.
Los cuerpos tienden, por inercia, a desplazarse en l nea recta a velocidad constante. Por lo tanto, si un cuerpo orbita alrededor de otro, se desviar de su trayectoria rectil nea y 'caer ' en una rbita. De manera similar, si no hay algo que retenga a un cuerpo, comenzar a alejarse de la rbita experimentando, para un objeto en el centro del sistema que rota, una aparente aceleraci n que lo aleja del centro, lo cual se conoce como aceleraci n centr fuga. La aceleraci n se define como:
La aceleraci n centr fuga es una aceleraci n que un sistema observa en el eje de rotaci n cuando un objeto se aleja (fuga) a velocidad constante. Para el objeto que se aleja, no existe dicha aceleraci n.
Si expresamos la velocidad tangencial en funci n de la velocidad angular, la aceleraci n centr fuga se calcula como:
Cuando un objeto orbita en un radio $r$ y tiene una velocidad tangencial $v$, mantiene de forma permanente una distancia al centro igual al radio.
Para un observador externo al sistema, el cuerpo, que por inercia viajar a en l nea recta, se desv a de esta trayectoria manteniendo la distancia al centro. Desde el punto de vista de este observador, el cuerpo est acelerando hacia el centro (centr peta) de la rbita. A diferencia de la aceleraci n centr fuga, el objeto est experimentando una aceleraci n real. La magnitud de esta aceleraci n es igual a la aceleraci n centr fuga, pero con el signo opuesto. Por lo tanto, la magnitud de la aceleraci n centr peta es:
A diferencia de la aceleraci n centr fuga, la aceleraci n centr peta es mensurable para el objeto que literalmente 'cae' hacia el centro.
Si dividimos la relaci n entre la distancia recorrida en un tiempo ($\Delta s$) y el radio ($r$) por la variación del angulo ($\Delta\theta$),
y luego dividimos eso por el tiempo transcurrido ($\Delta t$), obtenemos la relaci n que nos permite calcular la velocidad ($v$) a lo largo de la rbita, conocida como velocidad tangencial, que es igual a la velocidad angular ($\omega$):
Para describir el movimiento de un objeto, debemos calcular el tiempo transcurrido ($\Delta t$). Esta magnitud se obtiene midiendo el tiempo inicial ($t_0$) y el el tiempo ($t$) de dicho movimiento. La duraci n se determina restando el tiempo inicial al tiempo final:
Podemos calcular la distancia recorrida en un tiempo ($\Delta s$) a partir de la posición inicial ($s_0$) y la posición ($s$) mediante la siguiente ecuaci n:
Para describir la rotaci n de un objeto, es necesario determinar la variación del angulo ($\Delta\theta$). Esto se logra restando el ángulo inicial ($\theta_0$) del valor alcanzado por el objeto durante su rotaci n, que es el ángulo ($\theta$):
La velocidad media ($\bar{v}$) se puede calcular de la distancia recorrida en un tiempo ($\Delta s$) y el tiempo transcurrido ($\Delta t$) mediante:
Si la velocidad es constante, la velocidad ser igual a la velocidad inicial ($v_0$). En este caso, el camino recorrido en funci n del tiempo puede calcularse utilizando la diferencia entre la posición ($s$) y la posición inicial ($s_0$), dividida por la diferencia entre el tiempo ($t$) y el tiempo inicial ($t_0$):
La ecuaci n correspondiente define una l nea recta en el espacio-tiempo.
Para estimar el desplazamiento de un objeto, es necesario conocer su la velocidad angular ($\omega$) en funci n de el tiempo ($t$). Por lo tanto, se introduce la la velocidad angular media ($\bar{\omega}$), definida como la proporci n entre la variación del angulo ($\Delta\theta$) y el tiempo transcurrido ($\Delta t$).
Para medir esto, se puede utilizar un sistema como el que se muestra en la imagen:
Para determinar la velocidad angular media, se coloca un elemento reflectante en el eje o en un disco con varios elementos reflectantes, y se registra el paso para estimar la longitud del arco $\Delta s$ y el ngulo asociado con el radio $r$. Luego se registra la diferencia de tiempo cuando la marca pasa frente al sensor como $\Delta t$. La velocidad angular media se determina dividiendo el ngulo recorrido por el tiempo transcurrido.
La ecuaci n que describe la velocidad angular media es:
Cabe destacar que la velocidad media es una estimaci n de la velocidad angular real. El problema principal es que:
Si la velocidad angular var a durante el tiempo transcurrido, el valor de la velocidad angular media puede ser muy diferente de la velocidad angular promedio.
Por lo tanto, la clave es:
Determinar la velocidad en un tiempo transcurrido suficientemente corto para minimizar su variaci n.
En el caso de que la velocidad angular sea constante, la velocidad angular media ($\bar{\omega}$) coincide con el valor de la velocidad angular inicial ($\omega_0$), por lo que
En este caso, podemos calcular el ngulo recorrido en funci n del tiempo recordando que este se asocia a la diferencia entre el ngulo actual y el inicial, as como el tiempo actual y el inicial. Por lo tanto, el ángulo ($\theta$) es igual a el ángulo inicial ($\theta_0$), la velocidad angular inicial ($\omega_0$), el tiempo ($t$) y el tiempo inicial ($t_0$) como se muestra a continuaci n:
La ecuaci n representa una recta en el espacio ngulo-tiempo.
Cuando la velocidad angular es constante, es trivial que la velocidad angular media es igual a dicha velocidad angular constante. En otras palabras, la velocidad angular inicial ($\omega_0$) es igual a la velocidad angular media ($\bar{\omega}$):
Cuando la velocidad es constante, entonces es trivial que la velocidad media es igual a dicha velocidad constante. Es decir, la velocidad constante ($v_0$) es igual a la velocidad media ($\bar{v}$):
Como el per metro de un c rculo es $2\pi r$, ERROR:6294 a lo largo del c rculo corresponder al arco recorrido en el angulo que soporta el Arco ($\theta$), por lo que:
Como el per metro de un c rculo es $2\pi r$, ERROR:6294 a lo largo del c rculo corresponder al arco recorrido en el angulo que soporta el Arco ($\theta$), por lo que:
Como el per metro de un c rculo es $2\pi r$, ERROR:6294 a lo largo del c rculo corresponder al arco recorrido en el angulo que soporta el Arco ($\theta$), por lo que:
ID:(758, 0)