Usuario:
Arco recorrido al rotar
Definición 
Si se observa un círculo, su perímetro será $2\pi r$, con el radio ($r$). Si se tiene una variación del angulo ($\Delta\theta$), este representa una fracción de la circunferencia total, dada por la expresión:
$\displaystyle\frac{\Delta\theta}{2\pi}$
la distancia recorrida en un tiempo ($\Delta s$) correspondiente al arco bajo la variación del angulo ($\Delta\theta$) que se puede calcularse como esta fracción del perímetro total del círculo:
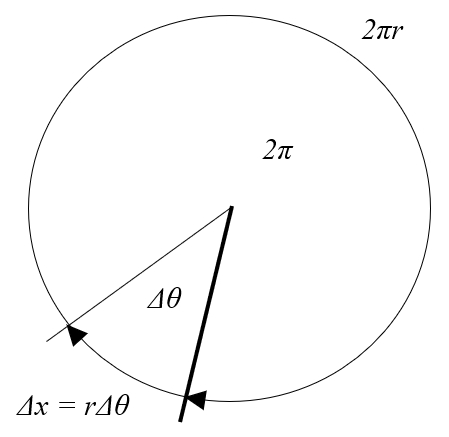
Para estos cálculos es clave que el ángulo se exprese en radianes.
ID:(9879, 0)
Arco
Descripción
Variables
Cálculos
a 
,
luego, seleccione la variable: 
a 
Cálculos
Variable
Dado
Calcule
Objetivo :
Ecuación
A utilizar
Ecuaciones
Si un objeto est a una distancia igual a el radio ($r$) de un eje y realiza una rotaci n en una variación del angulo ($\Delta\theta$), que con el ángulo ($\theta$) y el ángulo inicial ($\theta_0$) es
| $ \Delta\theta = \theta_2 - \theta_1 $ |
habr recorrido un arco la distancia recorrida en un tiempo ($\Delta s$), que con la posición ($s$) y la posición inicial ($s_0$) es
| $ \Delta s = s_2 - s_1 $ |
Dicho arco se puede calcular multiplicando el radio ($r$) por el ngulo, es decir,
| $ \Delta s=r \Delta\theta $ |
.
(ID 5302)
Ejemplos
Si se observa un c rculo, su per metro ser $2\pi r$, con el radio ($r$). Si se tiene una variación del angulo ($\Delta\theta$), este representa una fracci n de la circunferencia total, dada por la expresi n:
$\displaystyle\frac{\Delta\theta}{2\pi}$
la distancia recorrida en un tiempo ($\Delta s$) correspondiente al arco bajo la variación del angulo ($\Delta\theta$) que se puede calcularse como esta fracci n del per metro total del c rculo:
Para estos c lculos es clave que el ngulo se exprese en radianes.
(ID 9879)
La distancia recorrida en un tiempo ($\Delta s$) en un movimiento circular puede calcularse a partir de la variación del angulo ($\Delta\theta$) y el radio ($r$) de la rbita utilizando la siguiente f rmula:
| $ \Delta s=r \Delta\theta $ |
(ID 5302)
ID:(1449, 0)