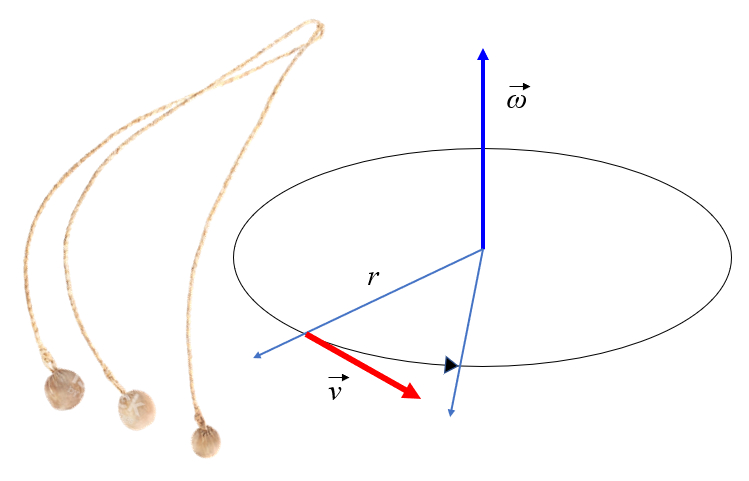
Accélération centrifuge et centripète
Storyboard 
Tout objet en mouvement rectiligne tend à se déplacer en ligne droite. Pour suivre une orbite circulaire, il est nécessaire que le corps "tombe" radicalement de sa trajectoire rectiligne jusqu'au rayon de l'orbite. Cette "chute" correspond à une accélération centripète (centri = centre, peta = vers), comme le percevrait un observateur externe au système.
En revanche, si l'objet continue son mouvement rectiligne au lieu de suivre l'orbite, pour un observateur dans le système rotatif, il percevra la même accélération mais en s'éloignant du centre, ce qui est appelé accélération centrifuge (centri = centre, fuga = en s'éloignant).
ID:(758, 0)
Accélération centrifuge et centripète
Storyboard 
Tout objet en mouvement rectiligne tend à se déplacer en ligne droite. Pour suivre une orbite circulaire, il est nécessaire que le corps "tombe" radicalement de sa trajectoire rectiligne jusqu'au rayon de l'orbite. Cette "chute" correspond à une accélération centripète (centri = centre, peta = vers), comme le percevrait un observateur externe au système. En revanche, si l'objet continue son mouvement rectiligne au lieu de suivre l'orbite, pour un observateur dans le système rotatif, il percevra la même accélération mais en s'éloignant du centre, ce qui est appelé accélération centrifuge (centri = centre, fuga = en s'éloignant).
Variables
Calculs
Calculs
Équations
Dans le cas o a vitesse angulaire initiale ($\omega_0$) est gal a vitesse angulaire moyenne ($\bar{\omega}$),
Par cons quent, avec a différence d'angles ($\Delta\theta$), qui est gal le angle ($\theta$) divis par le angle de départ ($\theta_0$), nous obtenons :
Et avec le temps écoulé ($\Delta t$), qui est gal le temps ($t$) divis par le temps initial ($t_0$), nous obtenons :
Nous pouvons r crire l' quation pour a vitesse angulaire moyenne ($\bar{\omega}$) comme suit :
Cela peut tre exprim comme suit :
$\omega_0 = \omega = \displaystyle\frac{\Delta\theta}{\Delta t} = \displaystyle\frac{\theta - \theta_0}{t - t_0}$
En r solvant cela, nous obtenons :
Avec a distance parcourue en un temps ($\Delta s$) c'est avec a position ($s$) et a vitesse ($s_0$) :
et le temps écoulé ($\Delta t$) est avec le temps ($t$) et le temps initial ($t_0$) :
L' quation pour la vitesse moyenne :
peut tre crite comme :
donc, en la r solvant, on obtient :
Comme a vitesse moyenne ($\bar{v}$) est avec a distance parcourue en un temps ($\Delta s$) et le temps écoulé ($\Delta t$), gal
et avec a distance parcourue en un temps ($\Delta s$) exprim comme un arc de cercle, et le radio ($r$) et a variation d'angle ($\Delta\theta$) sont
et la d finition de a vitesse angulaire moyenne ($\bar{\omega}$) est
alors,
$v=\displaystyle\frac{\Delta s}{\Delta t}=r\displaystyle\frac{\Delta\theta}{\Delta t}=r\omega$
Comme la relation est g n rale, elle peut tre appliqu e pour des valeurs instantan es, ce qui donne
La d finition de a vitesse angulaire moyenne ($\bar{\omega}$) est consid r e comme a variation d'angle ($\Delta\theta$),
et le temps écoulé ($\Delta t$),
La relation entre les deux est d finie comme a vitesse angulaire moyenne ($\bar{\omega}$) :
tant donn que l\'acc l ration centrifuge est gale
avec
nous pouvons en conclure que :
Si la distance parcourue est petite ($v\Delta t\ll r$), la racine carr e de la distance entre le centre et le corps,
$\sqrt{r^2+(v\Delta t)^2}$
,
peut tre approxim e par
$r+\displaystyle\frac{1}{2}\displaystyle\frac{v^2}{r}\Delta t^2$
,
ce qui correspond une parabole en fonction du temps $\Delta t$. Par cons quent, le comportement peut tre d crit avec une acc l ration gale :
Exemples
Si un objet est soumis un mode de maintien d'un rayon constant, il tournera comme indiqu dans la figure. En observant la figure, on remarquera que la masse effectue un mouvement de translation avec une vitesse tangentielle gale au rayon multipli par la vitesse angulaire:
Cependant, si l' l ment reliant l\'objet l\'axe est coup , l\'objet continuera se d placer tangentiellement en ligne droite.
Si un corps fix une corde de longueur $r$ tourne avec une vitesse tangentielle $v$ et que la corde est coup e, le corps continuera se d placer en ligne droite avec une vitesse constante $v$ en raison de l'inertie.
Dans un intervalle de temps $\Delta t$, le corps aura parcouru une distance de $v\Delta t$ de mani re tangentielle son orbite pr c dente. Du point de vue d'un observateur sur l\'axe du syst me en rotation, la distance est calcul e en utilisant le th or me de Pythagore, en ajoutant le carr du rayon de l\'orbite au carr de la distance parcourue :
$\sqrt{r^2+v^2\Delta t^2}$
Si nous tudions une catapulte, nous remarquerons que le projectile se d place d'abord le long de la courbe d crite par la cuill re. Cela se produit parce que la cuill re est con ue pour retenir le projectile. Une fois que le bras s'arr te, le projectile continue en ligne droite de mani re tangentielle au cercle qu\'il parcourait.
Si un corps n\'est pas retenu et se d place avec une vitesse tangentielle $v$, il parcourra en un temps $\Delta t$ la distance $v\Delta t$ en se d pla ant de B C. Cependant, s\'il continue orbiter, il atteindra le point D apr s le temps $\Delta t$. Si l\'objet atteint C, pour un observateur sur Terre, il y aura une acc l ration par laquelle un objet s\' loigne de la Terre (acc l ration centrifuge) en parcourant la distance $\Delta r$ en un temps $\Delta t$.
Pour un observateur dans l\'espace, un objet en mouvement dans l\'orbite est en chute permanente : au lieu de se terminer C, il chute sur la distance $\Delta r$ en un temps $\Delta t$ jusqu\' atteindre D. Dans les deux cas, nous pouvons repr senter la situation graphiquement et en utilisant le th or me de Pythagore, nous pouvons constater que l\' quation suivante doit tre satisfaite :
$(r+\Delta r)^2=r^2+(v\Delta t)^2$
Si nous d veloppons le carr de l\' quation, elle se r duit :
$2\Delta rr+\Delta r^2=v^2\Delta t^2$
Comme la variation du rayon $\Delta r$ est beaucoup plus petite que le rayon lui-m me ($r\ll\Delta r$), nous pouvons conclure que :
$2\Delta rr=v^2\Delta t^2$
ou en r solvant pour $\Delta r$:
$\Delta r=\displaystyle\frac{1}{2}\displaystyle\frac{v^2}{r}\Delta t^2$
En comparant cette quation l\' quation $s=at^2/2$, on conclut que le corps acc l re avec une acc l ration gale $v^2/r$.
Les corps ont tendance, par inertie, se d placer en ligne droite vitesse constante. Ainsi, si un corps orbite autour d'un autre, il d vie de sa trajectoire rectiligne et 'tombe' dans une orbite. De m me, si rien ne retient un corps, il commencera s\' loigner de l\'orbite, subissant, pour un objet au centre du syst me en rotation, une acc l ration apparente qui l\' loigne du centre, connue sous le nom d\'acc l ration centrifuge. L\'acc l ration est d finie comme suit :
L\'acc l ration centrifuge est une acc l ration observ e par un syst me sur l\'axe de rotation lorsqu\'un objet s\' loigne (fuit) vitesse constante. Pour l\'objet s\' loignant, cette acc l ration n\'existe pas.
Si la vitesse tangentielle est exprim e en fonction de la vitesse angulaire, l\'acc l ration centrifuge est donn e par:
Lorsqu'un objet orbite un rayon $r$ avec une vitesse tangentielle $v$, il maintient en permanence une distance constante par rapport au centre gale au rayon.
Pour un observateur externe au syst me, le corps, qui se d placerait en ligne droite par inertie, d vie de cette trajectoire tout en maintenant la distance par rapport au centre. Du point de vue de cet observateur, le corps acc l re vers le centre (acc l ration centrip te) de l'orbite. Contrairement l\'acc l ration centrifuge, l\'objet subit une v ritable acc l ration. La magnitude de cette acc l ration est gale l\'acc l ration centrifuge mais avec un signe oppos . Ainsi, la magnitude de l\'acc l ration centrip te est :
Contrairement l\'acc l ration centrifuge, l\'acc l ration centrip te est mesurable pour l\'objet qui est litt ralement \'attir \' vers le centre.
Si nous divisons la relation entre a distance parcourue en un temps ($\Delta s$) et le radio ($r$) par a variation d'angle ($\Delta\theta$),
et puis la divisons par le temps écoulé ($\Delta t$), nous obtenons la relation qui nous permet de calculer a vitesse ($v$) le long de l'orbite, connue sous le nom de vitesse tangentielle, qui est associ e a vitesse angulaire ($\omega$):
Pour d crire le mouvement d'un objet, nous devons calculer le temps écoulé ($\Delta t$). Cette grandeur est obtenue en mesurant le temps initial ($t_0$) et le le temps ($t$) de ce mouvement. La dur e est d termin e en soustrayant le temps initial du temps final :
Nous pouvons calculer a distance parcourue en un temps ($\Delta s$) partir de a vitesse ($s_0$) et a position ($s$) gr ce l' quation suivante :
Pour d crire la rotation d'un objet, nous devons d terminer a variation d'angle ($\Delta\theta$). Cela se fait en soustrayant le angle de départ ($\theta_0$) de le angle ($\theta$), la valeur atteinte par l'objet pendant sa rotation:
A vitesse moyenne ($\bar{v}$) peut tre calcul partir de a distance parcourue en un temps ($\Delta s$) et le temps écoulé ($\Delta t$) en utilisantxa0:
Si la vitesse est constante, la vitesse sera gale a vitesse initiale ($v_0$). Dans ce cas, la distance parcourue en fonction du temps peut tre calcul e en utilisant la diff rence entre a position ($s$) et a vitesse ($s_0$), divis e par la diff rence entre le temps ($t$) et le temps initial ($t_0$) :
L' quation correspondante d finit une ligne droite dans l'espace-temps.
Pour estimer le d placement d'un objet, il est n cessaire de conna tre sa a vitesse angulaire ($\omega$) en fonction de le temps ($t$). Ainsi, on introduit la a vitesse angulaire moyenne ($\bar{\omega}$), d finie comme le rapport entre a variation d'angle ($\Delta\theta$) et le temps écoulé ($\Delta t$).
Pour mesurer cela, on peut utiliser un syst me comme celui illustr sur l'image :
Pour d terminer la vitesse angulaire moyenne, on place un l ment r fl chissant sur l\'axe ou sur un disque avec plusieurs l ments r fl chissants, et on enregistre le passage pour estimer la longueur de l\'arc $\Delta s$ et l\'angle associ au rayon $r$. Ensuite, la diff rence de temps lorsque la marque passe devant le capteur est enregistr e comme $\Delta t$. La vitesse angulaire moyenne est d termin e en divisant l\'angle parcouru par le temps coul .
L\' quation qui d crit la vitesse angulaire moyenne est :
Il convient de noter que la vitesse moyenne est une estimation de la vitesse angulaire r elle. Le principal probl me est que :
Si la vitesse angulaire varie pendant le temps coul , la valeur de la vitesse angulaire moyenne peut tre tr s diff rente de la vitesse angulaire moyenne.
Par cons quent, la cl est :
D terminer la vitesse dans un temps coul suffisamment court pour minimiser sa variation.
Dans le cas o la vitesse angulaire est constante, a vitesse angulaire moyenne ($\bar{\omega}$) co ncide avec la valeur de a vitesse angulaire initiale ($\omega_0$), donc
Dans ce sc nario, nous pouvons calculer l'angle parcouru en fonction du temps en rappelant qu'il est associ la diff rence entre les angles actuel et initial, ainsi qu'entre le temps actuel et initial. Par cons quent, le angle ($\theta$) est gal le angle de départ ($\theta_0$), a vitesse angulaire initiale ($\omega_0$), le temps ($t$) et le temps initial ($t_0$) comme indiqu ci-dessous :
L' quation repr sente une droite dans l'espace angle-temps.
Lorsque la vitesse angulaire est constante, il est trivial que la vitesse angulaire moyenne soit gale cette vitesse angulaire constante. En d'autres termes, a vitesse angulaire initiale ($\omega_0$) est gal a vitesse angulaire moyenne ($\bar{\omega}$):
Lorsque la vitesse est constante, il est vident que la vitesse moyenne est gale cette vitesse constante. Autrement dit, a vitesse constante ($v_0$) est gal a vitesse moyenne ($\bar{v}$):
Comme le p rim tre d'un cercle est $2\pi r$, ERROR:6294 le long du cercle correspondra l'arc parcouru par ERROR:5059, donc :
Comme le p rim tre d'un cercle est $2\pi r$, ERROR:6294 le long du cercle correspondra l'arc parcouru par ERROR:5059, donc :
Comme le p rim tre d'un cercle est $2\pi r$, ERROR:6294 le long du cercle correspondra l'arc parcouru par ERROR:5059, donc :
ID:(758, 0)