Arc parcouru lors de la rotation
Définition 
Si l'on observe un cercle, son périmètre sera de $2\pi r$, avec le radio ($r$). Si l'on a une variation d'angle ($\Delta\theta$), cela représente une fraction du périmètre total, donnée par l'expression :
$\displaystyle\frac{\Delta\theta}{2\pi}$
a distance parcourue en un temps ($\Delta s$) correspondant à l'arc sous a variation d'angle ($\Delta\theta$) qui peut être calculé comme cette fraction du périmètre total du cercle :
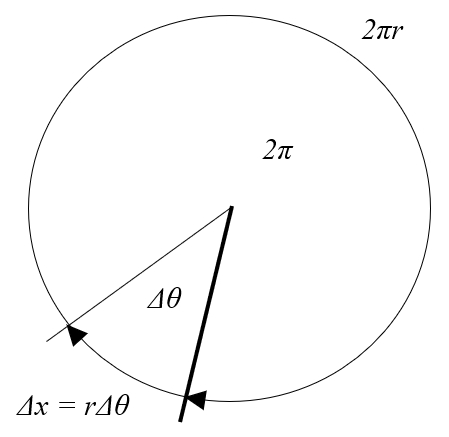
Pour ces calculs, il est crucial que l'angle soit exprimé en radians.
ID:(9879, 0)
Arc
Description 
Variables
Calculs
Calculs
Équations
Si un objet est une distance gale le radio ($r$) d'un axe et effectue une rotation en une variation d'angle ($\Delta\theta$), ce qui avec le angle ($\theta$) et le angle de départ ($\theta_0$) est
| $ \Delta\theta = \theta_2 - \theta_1 $ |
il aura parcouru un arc a distance parcourue en un temps ($\Delta s$), ce qui avec a position ($s$) et a vitesse ($s_0$) est
| $ \Delta s = s_2 - s_1 $ |
Cet arc peut tre calcul en multipliant le radio ($r$) par l'angle, c'est- -dire
| $ \Delta s=r \Delta\theta $ |
.
(ID 5302)
Exemples
Si l'on observe un cercle, son p rim tre sera de $2\pi r$, avec le radio ($r$). Si l'on a une variation d'angle ($\Delta\theta$), cela repr sente une fraction du p rim tre total, donn e par l'expression :
$\displaystyle\frac{\Delta\theta}{2\pi}$
a distance parcourue en un temps ($\Delta s$) correspondant l'arc sous a variation d'angle ($\Delta\theta$) qui peut tre calcul comme cette fraction du p rim tre total du cercle :

Pour ces calculs, il est crucial que l'angle soit exprim en radians.
(ID 9879)
La position a distance parcourue en un temps ($\Delta s$) dans un mouvement circulaire peut tre calcul e partir de a variation d'angle ($\Delta\theta$) et le radio ($r$) de l'orbite en utilisant la formule suivante :
| $ \Delta s=r \Delta\theta $ |
(ID 5302)
ID:(1449, 0)
