Benützer:
Der beim Drehen zurückgelegte Bogenmaß
Beschreibung 
Wenn man einen Kreis betrachtet, wird sein Umfang $2\pi r$ sein, mit der Radius ($r$). Wenn man eine Winkelvariation ($\Delta\theta$) hat, repräsentiert es einen Bruchteil des Gesamtumfangs, gegeben durch den Ausdruck:
$\displaystyle\frac{\Delta\theta}{2\pi}$
die Zurückgelegte Strecke in einer Zeit ($\Delta s$) entspricht dem Bogen unter die Winkelvariation ($\Delta\theta$), der als dieser Bruchteil des Gesamtumfangs des Kreises berechnet werden kann:
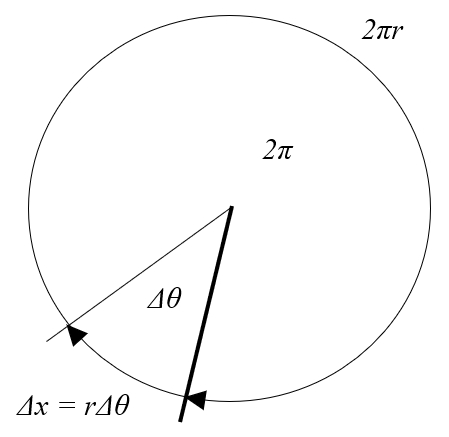
Für diese Berechnungen ist es entscheidend, dass der Winkel in Bogenmaß angegeben wird.
ID:(9879, 0)
Bogen zurückgelegt
Gleichung
Die Position die Zurückgelegte Strecke in einer Zeit ($\Delta s$) in einer Kreisbewegung kann aus die Winkelvariation ($\Delta\theta$) und der Radius ($r$) der Umlaufbahn mithilfe der folgenden Formel berechnet werden:
 $ \Delta s=r \Delta\theta $ |
Wenn ein Objekt einen Abstand von der Radius ($r$) von einer Achse entfernt ist und eine Drehung von eine Winkelvariation ($\Delta\theta$) durchführt, was mit der Winkel ($\theta$) und der Anfangswinkel ($\theta_0$) ergibt
| $ \Delta\theta = \theta - \theta_0 $ |
wird es eine Strecke von die Zurückgelegte Strecke in einer Zeit ($\Delta s$) zurückgelegt haben, was mit die Position ($s$) und die Ausgangsstellung ($s_0$) ergibt
| $ \Delta s \equiv s - s_0 $ |
Diese Strecke kann berechnet werden, indem man der Radius ($r$) mit dem Winkel multipliziert, also
| $ \Delta s=r \Delta\theta $ |
.
ID:(5302, 0)