Benützer:
Konstante Winkelgeschwindigkeit
Storyboard 
Um zu beschreiben, wie sich der Winkel im Laufe der Zeit entwickelt, ist es notwendig, seine Variation im Laufe der Zeit zu analysieren.
Die Beziehung zwischen der Veränderung des Winkels entspricht dem Winkel des zurückgelegten Bogens in der vergangenen Zeit, der, wenn er durch diese Zeit geteilt wird, zur Winkelgeschwindigkeit wird.
Wenn ein endliches Zeitintervall betrachtet wird, stellt die Winkelgeschwindigkeit die durchschnittliche Winkelgeschwindigkeit während dieses Intervalls dar.
ID:(611, 0)
Mechanismen
Konzept
Mechanismen
ID:(15409, 0)
Zurückgelegter Winkel
Beschreibung
Sobald das Konzept der vergangenen Zeit eingeführt wurde, kann die Bewegung in Bezug auf den zurückgelegten Winkel definiert werden. Dazu müssen wir Folgendes messen:
• den aktuellen Winkel, der als Winkeldifferenz zu einem Ursprungspunkt bestimmt wird, von dem aus wir messen;
• den Anfangswinkel, der als Winkeldifferenz zum gleichen vorherigen Ursprungspunkt bestimmt wird und als Differenz zwischen dem ersten und dem zweiten berechnet wird.
ID:(12516, 0)
Verstrichene Zeit
Konzept
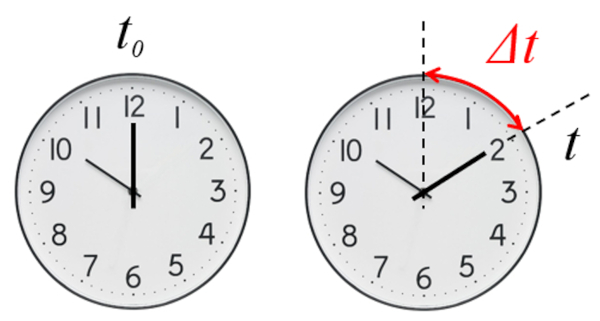
Die Grundlage für die Beschreibung jeder Entwicklung ist die Definition der Zeit, in der sie beschrieben wird. Insbesondere wird mit der Abgelaufene Zeit ($\Delta t$) seit einem Referenzzeitpunkt gearbeitet.
• Im Falle eines Stoppuhrs wird die verstrichene Zeit seit Beginn der Messung gemessen, d.h. eine Null-Startzeit ($t_0=0$).
• Im Falle einer Uhr wird die verstrichene Zeit seit einem definierten Startzeitpunkt gemessen, der null oder ungleich null sein kann.
ID:(12507, 0)
Konstante Winkelgeschwindigkeit
Konzept
Eine Situation, die auftreten kann, ist wenn die Winkelgeschwindigkeit konstant ist, was bedeutet, dass der zurückgelegte Winkel proportional zur verstrichenen Zeit zunimmt. Mit lässt sich dies folgendermaßen ausdrücken:
$\omega=\omega_0$
Es ist wichtig zu beachten, dass die Winkelgeschwindigkeit immer relativ zu einem Bezugssystem gemessen wird. In diesem Fall bezieht sich die konstante Winkelgeschwindigkeit auf das Bezugssystem, das für die Messung verwendet wird.
ID:(11410, 0)
Winkelgeschwindigkeit in grafischer Form
Beschreibung
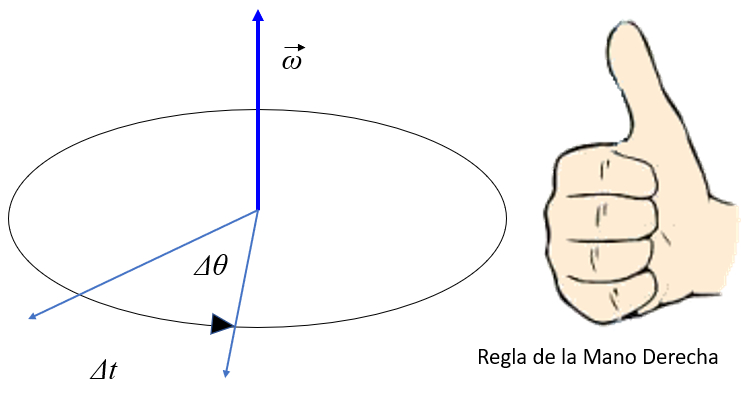
Die mittlere Winkelgeschwindigkeit wird als der im vergangenen Zeitraum zurückgelegte Winkel definiert. Da eine Drehung eine Achse erfordert, wird diese orthogonal zur Scheibe gezeichnet, die den rotierenden Körper darstellt. Um die Achse zu integrieren, wird die Winkelgeschwindigkeit als ein Vektor definiert, dessen Betrag der Winkel pro Zeiteinheit ist und dessen Richtung in Abhängigkeit von der Ausrichtung der Achse definiert ist:
ID:(10967, 0)
Winkel Zeit für konstante Winkelgeschwindigkeit und Anfangszeit
Bild
Um die gegebene Aussage auf Deutsch zu verbessern, schlage ich Folgendes vor:
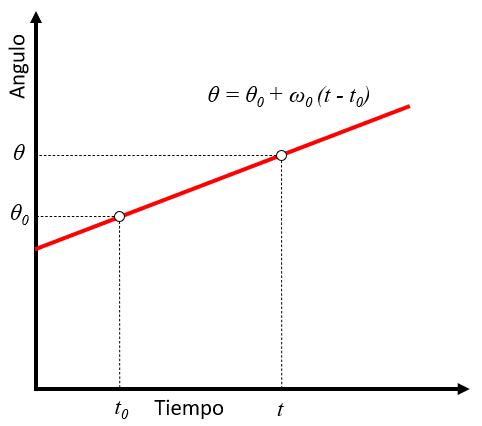
Im Fall von konstanter Winkelgeschwindigkeit und bekannter Anfangszeit kann der Winkel mithilfe der folgenden Formel berechnet werden:
| $ \theta = \theta_0 + \omega_0 ( t - t_0 )$ |
Die Formel wird graphisch wie folgt dargestellt:
Diese Formel ist nützlich, um den Winkel zu berechnen, den ein Objekt in Situationen gedreht hat, in denen sowohl die Winkelgeschwindigkeit als auch die Anfangszeit bekannt sind. Die Konstanz der Winkelgeschwindigkeit zeigt an, dass die Größe der Winkelgeschwindigkeit sich nicht mit der Zeit ändert. Die Anfangszeit ist die Referenzzeit, von der aus die verstrichene Zeit gemessen wird. Folglich kann der von dem Objekt gedrehte Winkel direkt berechnet werden, indem die Winkelgeschwindigkeit mit der verstrichenen Zeit seit der Anfangszeit multipliziert wird.
ID:(11412, 0)
Tangentialgeschwindigkeit
Beschreibung
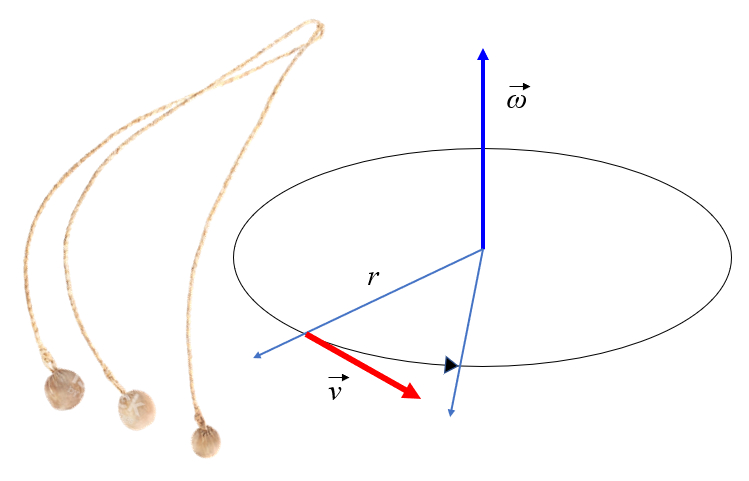
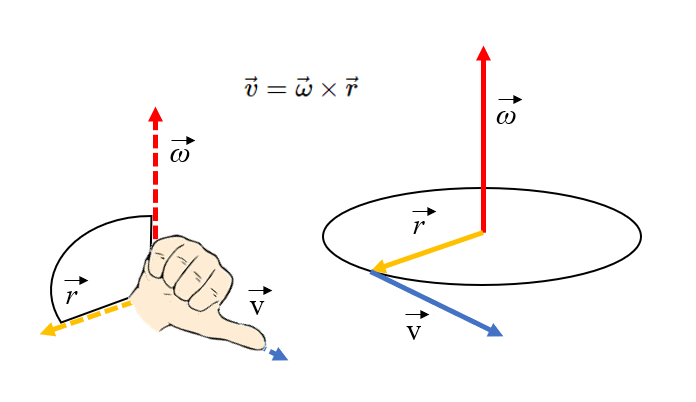
Wenn ein Objekt einem Modus unterworfen wird, um einen konstanten Radius beizubehalten, wird es sich wie in der Abbildung dargestellt drehen. Bei Betrachtung der Abbildung würde man bemerken, dass die Masse eine translatorische Bewegung mit einer tangentialen Geschwindigkeit ausführt, die dem Radius mal der Winkelgeschwindigkeit entspricht:
Wenn jedoch das Element, das das Objekt mit der Achse verbindet, abgeschnitten wird, wird sich das Objekt weiterhin tangential in einer geraden Linie bewegen.
ID:(310, 0)
Tangentialgeschwindigkeit, rechte Hand Regel
Bild
Die Orientierung der Tangentialgeschwindigkeit kann mit der Rechten-Hand-Regel bestimmt werden. Wenn die Finger in Richtung der Rotationsachse zeigen und dann in Richtung des Positionsvektors (Radius) gebogen werden, zeigt der Daumen in Richtung der Tangentialgeschwindigkeit:
ID:(11599, 0)
Modell
Konzept
Variablen
Parameter
Ausgewählter Parameter
Berechnungen
Gleichung
$ \Delta s=r \Delta\theta $
Ds = r * Dtheta
$ \Delta s \equiv s - s_0 $
Ds = s - s_0
$ \Delta t \equiv t - t_0 $
Dt = t - t_0
$ \Delta\theta = \theta - \theta_0 $
Dtheta = theta - theta_0
$ \bar{\omega} \equiv\displaystyle\frac{ \Delta\theta }{ \Delta t }$
omega_m = Dtheta / Dt
$ \bar{\omega} = \omega_0 $
omega_m = omega_0
$ \theta = \theta_0 + \omega_0 ( t - t_0 )$
theta = theta_0 + omega_0 * ( t - t_0 )
$ v_0 = r \omega_0 $
v = r * omega
$ \bar{v} \equiv\displaystyle\frac{ \Delta s }{ \Delta t }$
v_m = Ds / Dt
$ \bar{v} = v_0$
v_m = v_0
ID:(15420, 0)
Winkel Differenz
Gleichung
Um die Rotation eines Objekts zu beschreiben, müssen wir die Winkelvariation ($\Delta\theta$) bestimmen. Dies geschieht, indem wir der Anfangswinkel ($\theta_0$) von der Winkel ($\theta$) subtrahieren, den Wert, den das Objekt während seiner Rotation erreicht:
 $ \Delta\theta = \theta - \theta_0 $ |
ID:(3680, 0)
Verstrichenen Zeit
Gleichung
Um die Bewegung eines Objekts zu beschreiben, müssen wir die vergangene Zeit berechnen. Diese Größe wird durch Messung der Anfangszeit und der Endzeit der Bewegung ermittelt. Die Dauer wird durch Subtraktion der Anfangszeit von der Endzeit bestimmt.
Mathematisch wird dies als
| $ \Delta t \equiv t - t_0 $ |
dargestellt, wobei $\Delta t$ die Dauer, $t$ die Endzeit und $t_0$ die Anfangszeit ist.
ID:(4353, 0)
Mittlere Winkelgeschwindigkeit
Gleichung
Um die Verschiebung eines Objekts zu schätzen, ist es notwendig, seine die Winkelgeschwindigkeit ($\omega$) in Abhängigkeit von der Zeit ($t$) zu kennen. Daher wird die die Mittlere Winkelgeschwindigkeit ($\bar{\omega}$) eingeführt, die als das Verhältnis zwischen die Winkelvariation ($\Delta\theta$) und der Abgelaufene Zeit ($\Delta t$) definiert ist.
Um dies zu messen, kann ein System wie das im Bild gezeigt verwendet werden:
Um die durchschnittliche Winkelgeschwindigkeit zu bestimmen, wird ein reflektierendes Element auf der Achse oder auf einer Scheibe mit mehreren reflektierenden Elementen platziert, und der Durchgang wird erfasst, um die Länge des Bogens $\Delta s$ und den Winkel, der mit dem Radius $r$ verbunden ist, zu schätzen. Dann wird der Zeitunterschied aufgezeichnet, wenn die Markierung vor dem Sensor vorbeigeht, als $\Delta t$. Die durchschnittliche Winkelgeschwindigkeit wird durch die Division des zurückgelegten Winkels durch die verstrichene Zeit bestimmt.
Die Gleichung, die die durchschnittliche Winkelgeschwindigkeit beschreibt, lautet:
| $ \bar{\omega} \equiv\displaystyle\frac{ \Delta\theta }{ \Delta t }$ |
Die Definition von die Mittlere Winkelgeschwindigkeit ($\bar{\omega}$) wird als die Winkelvariation ($\Delta\theta$) betrachtet,
| $ \Delta\theta = \theta - \theta_0 $ |
und der Abgelaufene Zeit ($\Delta t$),
| $ \Delta t \equiv t - t_0 $ |
Die Beziehung zwischen beiden wird als die Mittlere Winkelgeschwindigkeit ($\bar{\omega}$) definiert:
| $ \bar{\omega} \equiv\displaystyle\frac{ \Delta\theta }{ \Delta t }$ |
Es ist zu beachten, dass die durchschnittliche Geschwindigkeit eine Schätzung der tatsächlichen Winkelgeschwindigkeit ist. Das Hauptproblem ist, dass:
Wenn sich die Winkelgeschwindigkeit während der verstrichenen Zeit ändert, kann der Wert der durchschnittlichen Winkelgeschwindigkeit sehr unterschiedlich zur durchschnittlichen Winkelgeschwindigkeit sein.
Daher ist der Schlüssel:
Die Geschwindigkeit in einer ausreichend kurzen verstrichenen Zeit zu bestimmen, um ihre Variation zu minimieren.
ID:(3679, 0)
Durchschnittliche und konstante Winkelgeschwindigkeit
Gleichung
Wenn die Winkelgeschwindigkeit konstant ist, ist es trivial, dass die mittlere Winkelgeschwindigkeit gleich dieser konstanten Winkelgeschwindigkeit ist. Mit anderen Worten, die Anfängliche Winkelgeschwindigkeit ($\omega_0$) ist gleich die Mittlere Winkelgeschwindigkeit ($\bar{\omega}$):
| $ \bar{\omega} = \omega_0 $ |
ID:(15431, 0)
Winkel für konstante Winkelgeschwindigkeit
Gleichung
Im Fall, dass die Winkelgeschwindigkeit konstant ist, fällt die Mittlere Winkelgeschwindigkeit ($\bar{\omega}$) mit dem Wert von die Anfängliche Winkelgeschwindigkeit ($\omega_0$) zusammen, daher
| $ \bar{\omega} = \omega_0 $ |
In diesem Fall können wir den Winkel als Funktion der Zeit berechnen, indem wir uns daran erinnern, dass er sich aus der Differenz zwischen dem aktuellen und dem Anfangswinkel sowie der aktuellen und der Anfangszeit ergibt. Daher ist der Winkel ($\theta$) gleich der Anfangswinkel ($\theta_0$), die Anfängliche Winkelgeschwindigkeit ($\omega_0$), der Zeit ($t$) und der Startzeit ($t_0$), wie unten gezeigt:
| $ \theta = \theta_0 + \omega_0 ( t - t_0 )$ |
Im Fall, dass die Anfängliche Winkelgeschwindigkeit ($\omega_0$) gleich die Mittlere Winkelgeschwindigkeit ($\bar{\omega}$) ist,
| $ \bar{\omega} = \omega_0 $ |
Deshalb erhalten wir mit die Differenz von Winkel ($\Delta\theta$), welches gleich der Winkel ($\theta$) geteilt durch der Anfangswinkel ($\theta_0$) ist:
| $ \Delta\theta = \theta - \theta_0 $ |
Und mit der Abgelaufene Zeit ($\Delta t$), welches gleich der Zeit ($t$) geteilt durch der Startzeit ($t_0$) ist:
| $ \Delta t \equiv t - t_0 $ |
Wir können die Gleichung für die Mittlere Winkelgeschwindigkeit ($\bar{\omega}$) umschreiben als:
| $ \bar{\omega} \equiv\displaystyle\frac{ \Delta\theta }{ \Delta t }$ |
Dies kann ausgedrückt werden als:
$\omega_0 = \omega = \displaystyle\frac{\Delta\theta}{\Delta t} = \displaystyle\frac{\theta - \theta_0}{t - t_0}$
Bei der Lösung erhalten wir:
| $ \theta = \theta_0 + \omega_0 ( t - t_0 )$ |
Die Gleichung stellt eine Gerade im Winkel-Zeit-Raum dar.
ID:(1023, 0)
Zurückgelegten Strecke
Gleichung
Wir können die Zurückgelegte Strecke in einer Zeit ($\Delta s$) aus die Ausgangsstellung ($s_0$) und die Position ($s$) berechnen mit der folgenden Gleichung:
| $ \Delta s \equiv s - s_0 $ |
ID:(4352, 0)
Durchschnittliche Geschwindigkeit
Gleichung
Die Mittlere Geschwindigkeit ($\bar{v}$) kann aus die Zurückgelegte Strecke in einer Zeit ($\Delta s$) und der Abgelaufene Zeit ($\Delta t$) berechnet werden mit:
| $ \bar{v} \equiv\displaystyle\frac{ \Delta s }{ \Delta t }$ |
ID:(3152, 0)
Durchschnittliche und konstante Geschwindigkeit
Gleichung
Wenn die Geschwindigkeit konstant ist, dann ist die durchschnittliche Geschwindigkeit trivialerweise gleich dieser konstanten Geschwindigkeit. Das heißt, die Konstante Geschwindigkeit ($v_0$) ist gleich die Mittlere Geschwindigkeit ($\bar{v}$):
| $ \bar{v} = v_0$ |
ID:(10276, 0)
Bogen zurückgelegt
Gleichung
Die Position die Zurückgelegte Strecke in einer Zeit ($\Delta s$) in einer Kreisbewegung kann aus die Winkelvariation ($\Delta\theta$) und der Radius ($r$) der Umlaufbahn mithilfe der folgenden Formel berechnet werden:
| $ \Delta s=r \Delta\theta $ |
Wenn ein Objekt einen Abstand von der Radius ($r$) von einer Achse entfernt ist und eine Drehung von eine Winkelvariation ($\Delta\theta$) durchführt, was mit der Winkel ($\theta$) und der Anfangswinkel ($\theta_0$) ergibt
| $ \Delta\theta = \theta - \theta_0 $ |
wird es eine Strecke von die Zurückgelegte Strecke in einer Zeit ($\Delta s$) zurückgelegt haben, was mit die Position ($s$) und die Ausgangsstellung ($s_0$) ergibt
| $ \Delta s \equiv s - s_0 $ |
Diese Strecke kann berechnet werden, indem man der Radius ($r$) mit dem Winkel multipliziert, also
| $ \Delta s=r \Delta\theta $ |
.
ID:(5302, 0)
Geschwindigkeit und Winkelgeschwindigkeit
Gleichung
Wenn wir das Verhältnis zwischen die Zurückgelegte Strecke in einer Zeit ($\Delta s$) und der Radius ($r$) durch die Winkelvariation ($\Delta\theta$) teilen,
| $ \Delta s=r \Delta\theta $ |
und das dann durch der Abgelaufene Zeit ($\Delta t$) teilen, erhalten wir die Beziehung, die es uns ermöglicht, die Geschwindigkeit ($v$) entlang der Umlaufbahn zu berechnen, bekannt als die tangentielle Geschwindigkeit, die mit die Winkelgeschwindigkeit ($\omega$) verbunden ist:
| $ v_0 = r \omega $ |
 $ v = r \omega $ |
Da die Mittlere Geschwindigkeit ($\bar{v}$) mit die Zurückgelegte Strecke in einer Zeit ($\Delta s$) und der Abgelaufene Zeit ($\Delta t$) gleich ist, was ist
| $ \bar{v} \equiv\displaystyle\frac{ \Delta s }{ \Delta t }$ |
und mit die Zurückgelegte Strecke in einer Zeit ($\Delta s$) als Bogen eines Kreises und der Radius ($r$) und die Winkelvariation ($\Delta\theta$) ist
| $ \Delta s=r \Delta\theta $ |
und die Definition von die Mittlere Winkelgeschwindigkeit ($\bar{\omega}$) ist
| $ \bar{\omega} \equiv\displaystyle\frac{ \Delta\theta }{ \Delta t }$ |
dann ist
$v=\displaystyle\frac{\Delta s}{\Delta t}=r\displaystyle\frac{\Delta\theta}{\Delta t}=r\omega$
Da die Beziehung allgemein ist, kann sie für momentane Werte angewendet werden, was zu
| $ v = r \omega $ |
führt.
ID:(3233, 0)