Zentrifugal- und Zentripetalbeschleunigung
Storyboard 
Ein Objekt mit Geschwindigkeit neigt dazu, sich geradlinig zu bewegen. Um eine kreisförmige Umlaufbahn zu verfolgen, muss ein Objekt "radikal" von seinem geraden Pfad zur Umlaufbahnradius abweichen. Dieser "Abfall" entspricht einer Zentripetalbeschleunigung (centri = Zentrum, petal = zum), wie sie von einem externen Beobachter des Systems wahrgenommen wird.
Andererseits, wenn das Objekt seinen geraden Pfad weiterverfolgt anstatt der kreisförmigen Umlaufbahn zu folgen, würde ein Beobachter im rotierenden System dieselbe Beschleunigung wahrnehmen, jedoch sich vom Zentrum entfernen. Dies wird als Zentrifugalbeschleunigung (centri = Zentrum, fuga = sich entfernend) bezeichnet.
ID:(758, 0)
Zentrifugal- und Zentripetalbeschleunigung
Storyboard 
Ein Objekt mit Geschwindigkeit neigt dazu, sich geradlinig zu bewegen. Um eine kreisförmige Umlaufbahn zu verfolgen, muss ein Objekt "radikal" von seinem geraden Pfad zur Umlaufbahnradius abweichen. Dieser "Abfall" entspricht einer Zentripetalbeschleunigung (centri = Zentrum, petal = zum), wie sie von einem externen Beobachter des Systems wahrgenommen wird. Andererseits, wenn das Objekt seinen geraden Pfad weiterverfolgt anstatt der kreisförmigen Umlaufbahn zu folgen, würde ein Beobachter im rotierenden System dieselbe Beschleunigung wahrnehmen, jedoch sich vom Zentrum entfernen. Dies wird als Zentrifugalbeschleunigung (centri = Zentrum, fuga = sich entfernend) bezeichnet.
Variablen
Berechnungen
Berechnungen
Gleichungen
Im Fall, dass die Anfängliche Winkelgeschwindigkeit ($\omega_0$) gleich die Mittlere Winkelgeschwindigkeit ($\bar{\omega}$) ist,
Deshalb erhalten wir mit die Differenz von Winkel ($\Delta\theta$), welches gleich der Winkel ($\theta$) geteilt durch der Anfangswinkel ($\theta_0$) ist:
Und mit der Abgelaufene Zeit ($\Delta t$), welches gleich der Zeit ($t$) geteilt durch der Startzeit ($t_0$) ist:
Wir k nnen die Gleichung f r die Mittlere Winkelgeschwindigkeit ($\bar{\omega}$) umschreiben als:
Dies kann ausgedr ckt werden als:
$\omega_0 = \omega = \displaystyle\frac{\Delta\theta}{\Delta t} = \displaystyle\frac{\theta - \theta_0}{t - t_0}$
Bei der L sung erhalten wir:
Mit die Zurückgelegte Strecke in einer Zeit ($\Delta s$) gleich die Position ($s$) und die Ausgangsstellung ($s_0$):
und der Abgelaufene Zeit ($\Delta t$) ist gleich der Zeit ($t$) und der Startzeit ($t_0$):
Die Gleichung f r die durchschnittliche Geschwindigkeit:
kann geschrieben werden als:
$v_0 = \bar{v} = \displaystyle\frac{\Delta s}{\Delta t} = \displaystyle\frac{s - s_0}{t - t_0}$
somit ergibt sich, wenn man nach ihr aufl st:
Da die Mittlere Geschwindigkeit ($\bar{v}$) mit die Zurückgelegte Strecke in einer Zeit ($\Delta s$) und der Abgelaufene Zeit ($\Delta t$) gleich ist, was ist
und mit die Zurückgelegte Strecke in einer Zeit ($\Delta s$) als Bogen eines Kreises und der Radius ($r$) und die Winkelvariation ($\Delta\theta$) ist
und die Definition von die Mittlere Winkelgeschwindigkeit ($\bar{\omega}$) ist
dann ist
$v=\displaystyle\frac{\Delta s}{\Delta t}=r\displaystyle\frac{\Delta\theta}{\Delta t}=r\omega$
Da die Beziehung allgemein ist, kann sie f r momentane Werte angewendet werden, was zu
f hrt.
Die Definition von die Mittlere Winkelgeschwindigkeit ($\bar{\omega}$) wird als die Winkelvariation ($\Delta\theta$) betrachtet,
und der Abgelaufene Zeit ($\Delta t$),
Die Beziehung zwischen beiden wird als die Mittlere Winkelgeschwindigkeit ($\bar{\omega}$) definiert:
Da die Zentrifugalbeschleunigung gleich
mit
k nnen wir folgern, dass:
Wenn die zur ckgelegte Strecke klein ist ($v\Delta t\ll r$), kann die Wurzel des Abstands zwischen dem Zentrum und dem K rper,
$\sqrt{r^2+(v\Delta t)^2}$
,
gen hert werden durch
$r+\displaystyle\frac{1}{2}\displaystyle\frac{v^2}{r}\Delta t^2$
,
was einer Parabel in Abh ngigkeit von der Zeit $\Delta t$ entspricht. Daher kann das Verhalten mit einer Beschleunigung beschrieben werden, die wie folgt lautet:
Beispiele
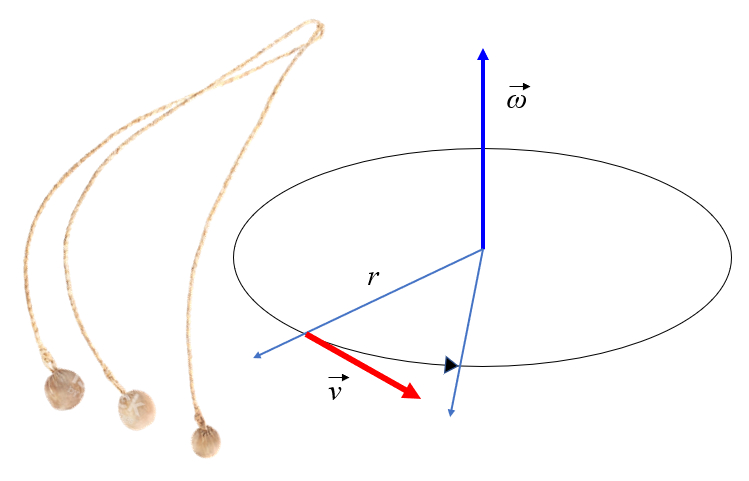
Wenn ein Objekt einem Modus unterworfen wird, um einen konstanten Radius beizubehalten, wird es sich wie in der Abbildung dargestellt drehen. Bei Betrachtung der Abbildung w rde man bemerken, dass die Masse eine translatorische Bewegung mit einer tangentialen Geschwindigkeit ausf hrt, die dem Radius mal der Winkelgeschwindigkeit entspricht:
Wenn jedoch das Element, das das Objekt mit der Achse verbindet, abgeschnitten wird, wird sich das Objekt weiterhin tangential in einer geraden Linie bewegen.
Wenn ein K rper, der an einem Seil der L nge $r$ befestigt ist, mit einer Tangentialgeschwindigkeit $v$ rotiert und das Seil durchtrennt wird, wird der K rper aufgrund der Tr gheit mit konstanter Geschwindigkeit $v$ in einer geraden Linie weiterbewegt.
In einem Zeitintervall $\Delta t$ wird der K rper eine Strecke von $v\Delta t$ tangential zu seiner vorherigen Bahn zur cklegen. Aus der Perspektive eines Beobachters auf der Achse des rotierenden Systems wird die Strecke mithilfe des Satzes des Pythagoras berechnet, indem das Quadrat des Bahnradius mit dem Quadrat der zur ckgelegten Strecke addiert wird:
$\sqrt{r^2+v^2\Delta t^2}$
Wenn wir eine Katapult betrachten, werden wir feststellen, dass das Projektil zun chst entlang der Kurve fliegt, die durch den L ffel beschrieben wird. Dies geschieht, weil der L ffel daf r konzipiert ist, das Projektil zur ckzuhalten. Sobald der Arm stoppt, bewegt sich das Projektil weiterhin in einer geraden Linie, die tangential zum Kreis verl uft, dem es zuvor gefolgt ist.
Wenn ein Objekt nicht zur ckgehalten wird und sich mit einer tangentialen Geschwindigkeit $v$ bewegt, legt es in einem Zeitintervall $\Delta t$ eine Strecke von $v\Delta t$ zur ck, indem es sich von Punkt B nach Punkt C bewegt. Wenn es jedoch weiterhin eine Umlaufbahn beibeh lt, erreicht es nach dem Zeitintervall $\Delta t$ den Punkt D. Wenn das Objekt den Punkt C erreicht, gibt es aus der Perspektive eines Beobachters auf der Erde eine Beschleunigung, die bewirkt, dass sich das Objekt von der Erde entfernt (Zentrifugalbeschleunigung) und dabei die Strecke $\Delta r$ im Zeitintervall $\Delta t$ zur cklegt.
F r einen Beobachter im Weltraum f llt ein Objekt in einer Umlaufbahn st ndig: Anstatt den Punkt C zu erreichen, f llt es im Zeitintervall $\Delta t$ ber die Strecke $\Delta r$ bis es den Punkt D erreicht. In beiden F llen k nnen wir die Situation graphisch darstellen und unter Verwendung des Satzes des Pythagoras feststellen, dass folgende Gleichung gelten muss:
$(r+\Delta r)^2=r^2+(v\Delta t)^2$
Durch Aufl sen der Gleichung ergibt sich:
$2\Delta rr+\Delta r^2=v^2\Delta t^2$
Da die Variation des Radius $\Delta r$ viel kleiner ist als der Radius selbst ($r\ll\Delta r$), k nnen wir schlussfolgern, dass gilt:
$2\Delta rr=v^2\Delta t^2$
Wenn wir nach $\Delta r$ aufl sen, erhalten wir:
$\Delta r=\displaystyle\frac{1}{2}\displaystyle\frac{v^2}{r}\Delta t^2$
Wenn wir diese Gleichung mit der Gleichung $s=at^2/2$ vergleichen, k nnen wir feststellen, dass das Objekt mit einer Beschleunigung von $v^2/r$ beschleunigt.
K rper tendieren aufgrund ihrer Tr gheit dazu, sich mit konstanter Geschwindigkeit entlang einer geraden Linie zu bewegen. Daher weicht ein K rper, der einen anderen umkreist, von seinem geraden Pfad ab und 'f llt' in eine Umlaufbahn. Ebenso wird ein K rper, wenn nichts ihn festh lt, beginnen, sich von der Umlaufbahn zu entfernen und dabei f r ein Objekt im Zentrum des rotierenden Systems eine scheinbare Beschleunigung erfahren, die es vom Zentrum wegf hrt - dies nennt man Zentrifugalbeschleunigung. Die Beschleunigung wird definiert als:
Die Zentrifugalbeschleunigung ist eine Beschleunigung, die von einem System in der Rotationsachse beobachtet wird, wenn sich ein Objekt mit konstanter Geschwindigkeit entfernt (flieht). F r das sich entfernde Objekt existiert eine solche Beschleunigung nicht.
Wenn wir die Tangentialgeschwindigkeit in Bezug auf die Winkelgeschwindigkeit ausdr cken, ergibt sich die Zentrifugalbeschleunigung zu:
Wenn ein Objekt mit einem Radius $r$ und einer Tangentialgeschwindigkeit $v$ in einer Umlaufbahn ist, bleibt es dauerhaft in einem Abstand zum Zentrum, der gleich dem Radius ist.
F r einen externen Beobachter des Systems weicht der K rper, der sich aufgrund seiner Tr gheit eigentlich in einer geraden Linie bewegen w rde, von dieser Bahn ab und h lt dabei den Abstand zum Zentrum ein. Aus Sicht dieses Beobachters beschleunigt der K rper zum Zentrum hin (Zentripetalbeschleunigung) der Umlaufbahn. Im Gegensatz zur Zentrifugalbeschleunigung erf hrt das Objekt eine reale Beschleunigung. Die Gr e dieser Beschleunigung ist gleich der Zentrifugalbeschleunigung, aber mit umgekehrtem Vorzeichen. Daher ist die Betragsgr e der Zentripetalbeschleunigung:
Im Gegensatz zur Zentrifugalbeschleunigung ist die Zentripetalbeschleunigung f r das Objekt messbar, das buchst blich zum Zentrum 'f llt'.
Wenn wir das Verh ltnis zwischen die Zurückgelegte Strecke in einer Zeit ($\Delta s$) und der Radius ($r$) durch die Winkelvariation ($\Delta\theta$) teilen,
und das dann durch der Abgelaufene Zeit ($\Delta t$) teilen, erhalten wir die Beziehung, die es uns erm glicht, die Geschwindigkeit ($v$) entlang der Umlaufbahn zu berechnen, bekannt als die tangentielle Geschwindigkeit, die mit die Winkelgeschwindigkeit ($\omega$) verbunden ist:
Um die Bewegung eines Objekts zu beschreiben, m ssen wir der Abgelaufene Zeit ($\Delta t$) berechnen. Diese Gr e wird durch Messung von der Startzeit ($t_0$) und der der Zeit ($t$) dieser Bewegung erhalten. Die Dauer wird bestimmt, indem die Anfangszeit von der Endzeit subtrahiert wird:
Wir k nnen die Zurückgelegte Strecke in einer Zeit ($\Delta s$) aus die Ausgangsstellung ($s_0$) und die Position ($s$) berechnen mit der folgenden Gleichung:
Um die Rotation eines Objekts zu beschreiben, m ssen wir die Winkelvariation ($\Delta\theta$) bestimmen. Dies geschieht, indem wir der Anfangswinkel ($\theta_0$) von der Winkel ($\theta$) subtrahieren, den Wert, den das Objekt w hrend seiner Rotation erreicht:
Die Mittlere Geschwindigkeit ($\bar{v}$) kann aus die Zurückgelegte Strecke in einer Zeit ($\Delta s$) und der Abgelaufene Zeit ($\Delta t$) berechnet werden mit:
Wenn die Geschwindigkeit konstant ist, wird die Geschwindigkeit gleich die Anfangsgeschwindigkeit ($v_0$) sein. In diesem Fall kann der zur ckgelegte Weg in Abh ngigkeit von der Zeit berechnet werden, indem die Differenz zwischen die Position ($s$) und die Ausgangsstellung ($s_0$) durch die Differenz zwischen der Zeit ($t$) und der Startzeit ($t_0$) geteilt wird:
Die entsprechende Gleichung definiert eine gerade Linie im Raum-Zeit-Kontinuum.
Um die Verschiebung eines Objekts zu sch tzen, ist es notwendig, seine die Winkelgeschwindigkeit ($\omega$) in Abh ngigkeit von der Zeit ($t$) zu kennen. Daher wird die die Mittlere Winkelgeschwindigkeit ($\bar{\omega}$) eingef hrt, die als das Verh ltnis zwischen die Winkelvariation ($\Delta\theta$) und der Abgelaufene Zeit ($\Delta t$) definiert ist.
Um dies zu messen, kann ein System wie das im Bild gezeigt verwendet werden:
Um die durchschnittliche Winkelgeschwindigkeit zu bestimmen, wird ein reflektierendes Element auf der Achse oder auf einer Scheibe mit mehreren reflektierenden Elementen platziert, und der Durchgang wird erfasst, um die L nge des Bogens $\Delta s$ und den Winkel, der mit dem Radius $r$ verbunden ist, zu sch tzen. Dann wird der Zeitunterschied aufgezeichnet, wenn die Markierung vor dem Sensor vorbeigeht, als $\Delta t$. Die durchschnittliche Winkelgeschwindigkeit wird durch die Division des zur ckgelegten Winkels durch die verstrichene Zeit bestimmt.
Die Gleichung, die die durchschnittliche Winkelgeschwindigkeit beschreibt, lautet:
Es ist zu beachten, dass die durchschnittliche Geschwindigkeit eine Sch tzung der tats chlichen Winkelgeschwindigkeit ist. Das Hauptproblem ist, dass:
Wenn sich die Winkelgeschwindigkeit w hrend der verstrichenen Zeit ndert, kann der Wert der durchschnittlichen Winkelgeschwindigkeit sehr unterschiedlich zur durchschnittlichen Winkelgeschwindigkeit sein.
Daher ist der Schl ssel:
Die Geschwindigkeit in einer ausreichend kurzen verstrichenen Zeit zu bestimmen, um ihre Variation zu minimieren.
Im Fall, dass die Winkelgeschwindigkeit konstant ist, f llt die Mittlere Winkelgeschwindigkeit ($\bar{\omega}$) mit dem Wert von die Anfängliche Winkelgeschwindigkeit ($\omega_0$) zusammen, daher
In diesem Fall k nnen wir den Winkel als Funktion der Zeit berechnen, indem wir uns daran erinnern, dass er sich aus der Differenz zwischen dem aktuellen und dem Anfangswinkel sowie der aktuellen und der Anfangszeit ergibt. Daher ist der Winkel ($\theta$) gleich der Anfangswinkel ($\theta_0$), die Anfängliche Winkelgeschwindigkeit ($\omega_0$), der Zeit ($t$) und der Startzeit ($t_0$), wie unten gezeigt:
Die Gleichung stellt eine Gerade im Winkel-Zeit-Raum dar.
Wenn die Winkelgeschwindigkeit konstant ist, ist es trivial, dass die mittlere Winkelgeschwindigkeit gleich dieser konstanten Winkelgeschwindigkeit ist. Mit anderen Worten, die Anfängliche Winkelgeschwindigkeit ($\omega_0$) ist gleich die Mittlere Winkelgeschwindigkeit ($\bar{\omega}$):
Wenn die Geschwindigkeit konstant ist, dann ist die durchschnittliche Geschwindigkeit trivialerweise gleich dieser konstanten Geschwindigkeit. Das hei t, die Konstante Geschwindigkeit ($v_0$) ist gleich die Mittlere Geschwindigkeit ($\bar{v}$):
Da der Umfang eines Kreises $2\pi r$ betr gt, entspricht ERROR:6294 entlang des Kreises dem Bogen, der durch ERROR:5059 berspannt wird, daher:
Da der Umfang eines Kreises $2\pi r$ betr gt, entspricht ERROR:6294 entlang des Kreises dem Bogen, der durch ERROR:5059 berspannt wird, daher:
Da der Umfang eines Kreises $2\pi r$ betr gt, entspricht ERROR:6294 entlang des Kreises dem Bogen, der durch ERROR:5059 berspannt wird, daher:
ID:(758, 0)