Constant angular speed
Storyboard 
To describe how the angle evolves over time, it's necessary to analyze its variation throughout time.
The relationship between the change in angle equals the arc angle traveled in the elapsed time, which, when divided by that time, becomes the angular velocity.
When considering a finite time interval, the angular velocity represents the average angular velocity during that interval.
ID:(611, 0)
Constant angular speed
Storyboard 
To describe how the angle evolves over time, it's necessary to analyze its variation throughout time. The relationship between the change in angle equals the arc angle traveled in the elapsed time, which, when divided by that time, becomes the angular velocity. When considering a finite time interval, the angular velocity represents the average angular velocity during that interval.
Variables
Calculations
Calculations
Equations
In the case where the initial Angular Speed ($\omega_0$) is equal to the mean angular velocity ($\bar{\omega}$),
Therefore, with the difference of Angles ($\Delta\theta$), which is equal to the angle ($\theta$) divided by the initial Angle ($\theta_0$), we obtain:
And with the time elapsed ($\Delta t$), which is equal to the time ($t$) divided by the start Time ($t_0$), we obtain:
We can rewrite the equation for the mean angular velocity ($\bar{\omega}$) as:
This can be expressed as:
$\omega_0 = \omega = \displaystyle\frac{\Delta\theta}{\Delta t} = \displaystyle\frac{\theta - \theta_0}{t - t_0}$
Solving for it, we get:
As the mean Speed ($\bar{v}$) is with the distance traveled in a time ($\Delta s$) and the time elapsed ($\Delta t$), equal to
and with the distance traveled in a time ($\Delta s$) expressed as an arc of a circle, and the radius ($r$) and the angle variation ($\Delta\theta$) are
and the definition of the mean angular velocity ($\bar{\omega}$) is
then,
$v=\displaystyle\frac{\Delta s}{\Delta t}=r\displaystyle\frac{\Delta\theta}{\Delta t}=r\omega$
Since the relationship is general, it can be applied for instantaneous values, resulting in
The definition of the mean angular velocity ($\bar{\omega}$) is considered as the angle variation ($\Delta\theta$),
and the time elapsed ($\Delta t$),
The relationship between both is defined as the mean angular velocity ($\bar{\omega}$):
If an object is at a distance equal to the radius ($r$) from an axis and rotates by ERROR:6066.1, which with the angle ($\theta$) and the initial Angle ($\theta_0$) is
it will have traveled an arc length the distance traveled in a time ($\Delta s$), which with the position ($s$) and the starting position ($s_0$) is
This arc length can be calculated by multiplying the radius ($r$) by the angle, that is,
Examples
Once the concept of elapsed time has been introduced, the motion can be defined in terms of the angle traveled. To do this, we need to measure:
• the current angle, which is determined as the angle difference to an origin from which we are measuring;
• the initial angle, which is determined as the angle difference to the same previous origin, and is calculated as the difference between the first and second.
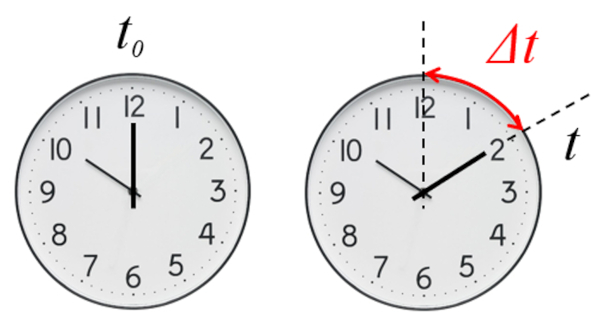
The foundation of describing any evolution is the definition of time in which it is described. Specifically, we work with the time elapsed ($\Delta t$) from a reference time.
The stopwatch directly gives us the elapsed time since its initial time is zero
In the case of a stopwatch, the elapsed time is measured from the start of its measurement, i.e., a zero initial time ($t_0=0$).
In the case of the clock, it is necessary to define the initial type in order to determine the elapsed time.
In the case of a clock, the elapsed time is measured from a defined initial time, which may or may not be zero.
Since the time elapsed ($\Delta t$) is calculated as the difference between the time ($t$) and the start Time ($t_0$):
it is possible to "shift" the time origin by adding a constant value
to both time points:
$t \rightarrow t + \tau$
$t_0 \rightarrow t_0 + \tau$
without affecting the elapsed time:
$\Delta t = t - t_0 \rightarrow (t + \tau) - (t_0 + \tau) = t - t_0 = \Delta t$
This property is known as temporal invariance, meaning that the elapsed time remains unchanged regardless of the specific starting point of the measurement.
Consequently, laws formulated using this principle will be temporally invariant, meaning they remain valid whether applied in the present, the past, or the future.
A situation that can arise is when the angular velocity is constant, which means that the angle covered increases proportionally to the elapsed time. In other words, using
$\omega=\omega_0$
It is important to note that angular velocity is always measured relative to a reference frame. In this case, the constant angular velocity is with respect to the reference frame being used for measurement.
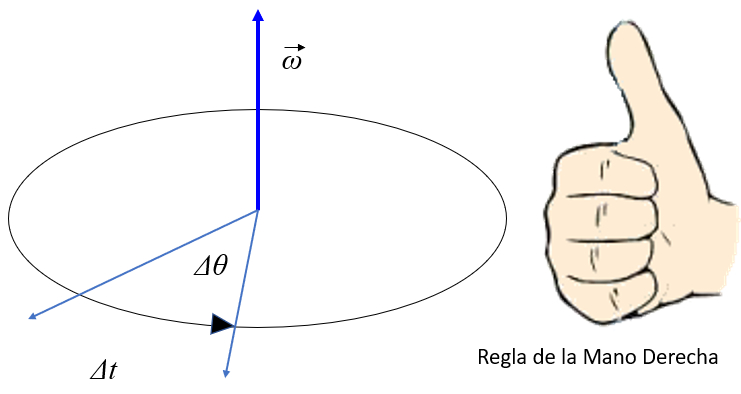
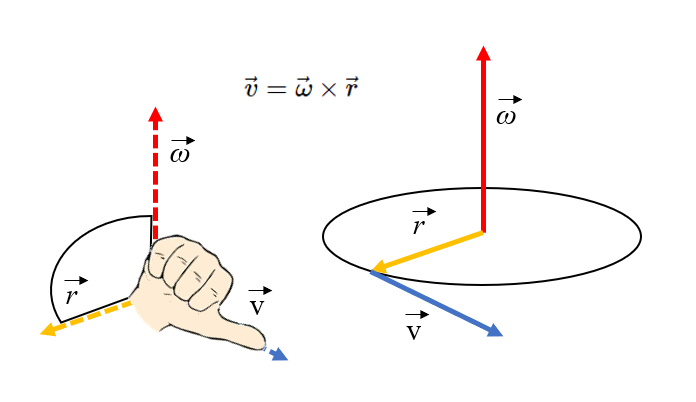
The average angular velocity is defined as the angle traversed in the elapsed time. As rotation requires an axis, it is drawn orthogonal to the disk that represents the rotating body. To integrate the axis, the angular velocity is defined as a vector in which the magnitude is the angle traversed per unit of time and the direction is defined based on the direction of the axis:
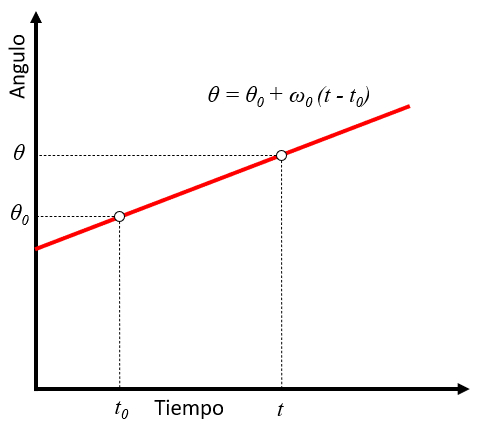
In the case of constant angular velocity and known initial time, the angle can be calculated using the following formula:
The formula is graphically represented below:
This formula is useful for calculating the angle rotated by an object in situations where both the angular velocity and initial time are known. The constancy of the angular velocity indicates that the magnitude of the angular velocity does not change with time. The initial time is the reference time from which the elapsed time is measured. Therefore, the angle rotated by the object can be calculated directly by multiplying the angular velocity by the elapsed time from the initial time.
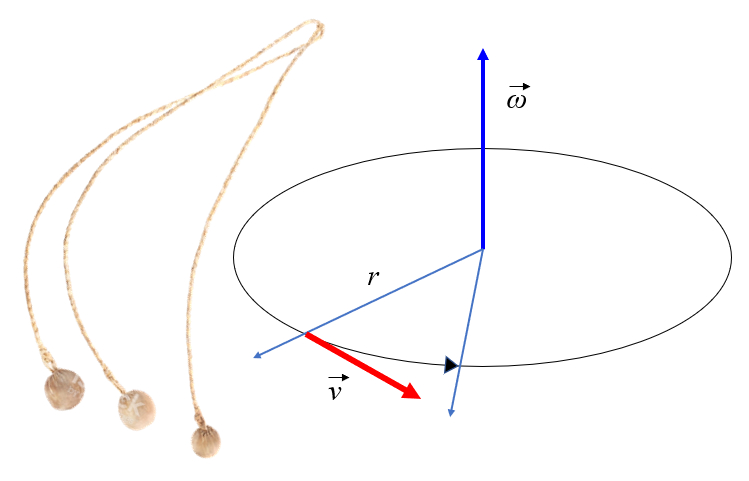
If an object is subjected to a mode of maintaining a constant radius, it will rotate as indicated in the figure. Upon observing the figure, one would notice that the mass undergoes a translational motion with a tangential velocity that is equal to the radius times the angular velocity:
However, if the element connecting the object to the axis is cut, the object will continue to move tangentially in a straight line.
The orientation of the tangential velocity can be obtained using the right-hand rule. If the fingers point towards the axis of rotation and then are curled towards the position vector (radius), the thumb will point in the direction of the tangential velocity:
To describe the rotation of an object, we need to determine the angle variation ($\Delta\theta$). This is achieved by subtracting the initial Angle ($\theta_0$) from the angle ($\theta$), which is reached by the object during its rotation:
To describe the motion of an object, we need to calculate the time elapsed ($\Delta t$). This magnitude is obtained by measuring the start Time ($t_0$) and the the time ($t$) of said motion. The duration is determined by subtracting the initial time from the final time:
To estimate the displacement of an object, it's necessary to know its the angular Speed ($\omega$) as a function of the time ($t$). Therefore, the the mean angular velocity ($\bar{\omega}$) is introduced, defined as the ratio between the angle variation ($\Delta\theta$) and the time elapsed ($\Delta t$).
To measure this, a system like the one shown in the image can be used:
To determine the average angular velocity, a reflective element is placed on the axis or on a disk with several reflective elements, and the passage is recorded to estimate the length of the arc $\Delta s$ and the angle associated with the radius $r$. Then the time difference when the mark passes in front of the sensor is recorded as $\Delta t$. The average angular velocity is determined by dividing the angle traveled by the time elapsed.
The equation that describes the average angular velocity is:
It should be noted that the average velocity is an estimation of the actual angular velocity. The main problem is that:
If the angular velocity varies during the elapsed time, the value of the average angular velocity can be very different from the average angular velocity.
Therefore, the key is:
Determine the velocity in a sufficiently short elapsed time to minimize its variation.
In the case where the angular velocity is constant, the mean angular velocity ($\bar{\omega}$) coincides with the value of the initial Angular Speed ($\omega_0$), so
In this scenario, we can calculate the angle traveled as a function of time by recalling that it is associated with the difference between the current and initial angles, as well as the current and initial time. Therefore, the angle ($\theta$) is equal to the initial Angle ($\theta_0$), the initial Angular Speed ($\omega_0$), the time ($t$), and the start Time ($t_0$) as shown below:
The equation represents a straight line in angle-time space.
We can calculate the distance traveled in a time ($\Delta s$) from the starting position ($s_0$) and the position ($s$) using the following equation:
The mean Speed ($\bar{v}$) can be calculated from the distance traveled in a time ($\Delta s$) and the time elapsed ($\Delta t$) using:
The position the distance traveled in a time ($\Delta s$) in a circular motion can be calculated from the angle variation ($\Delta\theta$) and the radius ($r$) of the orbit using the following formula:
Since the perimeter of a circle is $2\pi r$, ERROR:6294 along the circle will correspond to the arc spanned by ERROR:5059, so:
Since the perimeter of a circle is $2\pi r$, ERROR:6294 along the circle will correspond to the arc spanned by ERROR:5059, so:
If we divide the relationship between the distance traveled in a time ($\Delta s$) and the radius ($r$) by the angle variation ($\Delta\theta$),
and then divide it by the time elapsed ($\Delta t$), we obtain the relationship that allows us to calculate the speed ($v$) along the orbit, known as the tangential velocity, which is associated with the angular Speed ($\omega$):
ID:(611, 0)