Wasserdampf auf dem Boden
Storyboard 
Normalerweise ist der Druck des realen Wasserdampfs niedriger als das Maximum, das er der Luft widerstehen kann, bevor sie zu kondensieren beginnt. Daher wird das Konzept der relativen Luftfeuchtigkeit eingeführt.
ID:(377, 0)
Gasphase, Wasserdampf
Konzept 
Die gasförmige Phase, die in unserem Fall Wasserdampf entspricht, ist die Phase, in der Atome sich relativ frei bewegen können.
In dieser Phase gibt es nur minimale Wechselwirkungen, die das Verhalten der Atome beeinflussen können, ohne sie signifikant einzuschränken.
ID:(15142, 0)
Flüssige Phase, Wasser
Konzept 
Die flüssige Phase, die in unserem Fall Wasser entspricht, ist die Phase, in der Atome sich relativ frei bewegen können, dabei jedoch ihre Einheit beibehalten und sich der Form anpassen, die sie umgibt.

In dieser Phase wird keine spezifische Struktur beobachtet.
ID:(15140, 0)
Feste Phase, Eis
Konzept 
Die feste Phase, die in unserem Fall dem Eis entspricht, ist die Phase, in der sich Atome nicht relativ bewegen können und nur um ihren Gleichgewichtspunkt schwingen können.

In dieser Phase kann man eine Struktur beobachten, die oft kristallin und daher regelmäßig ist.
ID:(15141, 0)
Phasendiagramm des Wassers
Konzept 
Eines der relevantesten Phasendiagramme für unseren Planeten ist das des Wassers. Dieses Diagramm zeigt die drei klassischen Phasen: fest, flüssig und gasförmig, sowie verschiedene Phasen mit unterschiedlichen kristallinen Strukturen des Eises.
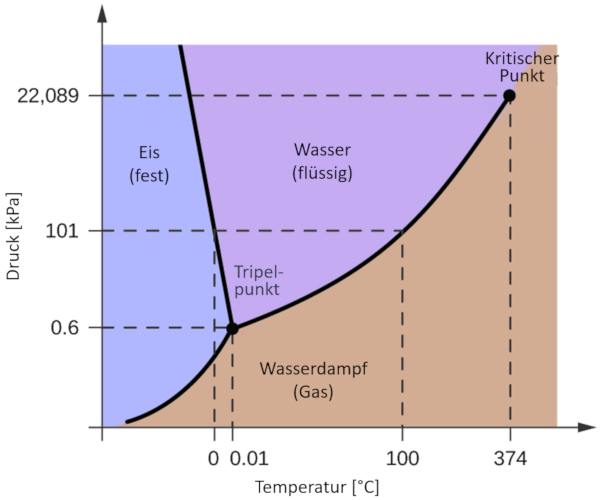
Der bedeutende Unterschied zu anderen Materialien besteht darin, dass im Druckbereich von 611 Pa bis 209,9 MPa die feste Phase ein größeres Volumen einnimmt als die flüssige Phase. Diese Eigenschaft spiegelt sich im Phasendiagramm als eine negative Neigung entlang der Grenzlinie zwischen der festen Phase (hexagonales Eis) und der flüssigen Phase (Wasser) wider.
ID:(836, 0)
Verdampfungswärmemessung
Konzept 
Die Messung der Verdampfungsenthalpie erfolgt durch Erwärmen einer Probe, wodurch sie verdampft, während gleichzeitig die zugeführte Wärme gemessen wird. Anschließend wird der erzeugte Dampf gekühlt und kondensiert, wobei die Masse gemessen wird, die ursprünglich verdampft ist.
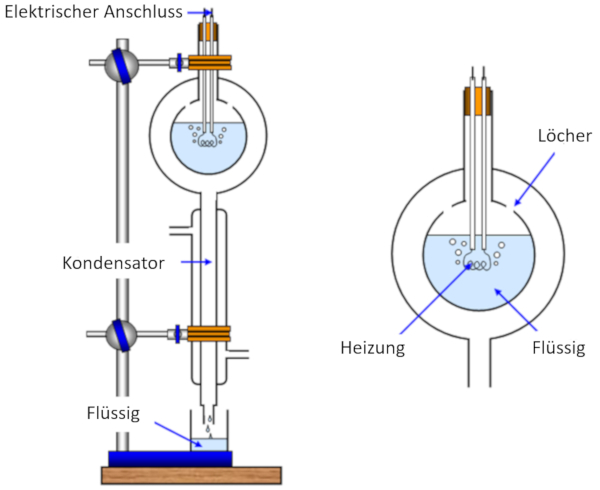
Auf diese Weise können wir die für die Verdampfung einer gegebenen Masse benötigte Energie abschätzen, die in ERROR:5238,0 gemessen wird, und zwar in Joule pro Kilogramm (J/kg) oder Joule pro Mol (J/mol).
ID:(1662, 0)
Wasserdampf
Konzept 
Die gasförmige Phase des Wassers entspricht dem, was als Wasserdampf bekannt ist. Diese entsteht, wenn Wassermoleküle genügend kinetische Energie erhalten, um aus der flüssigen Phase zu entweichen und sich im Raum über der Flüssigkeit zu bewegen. Periodisch kollidieren die Moleküle im gasförmigen Zustand erneut mit der Oberfläche der Flüssigkeit und werden erfasst, kehren in den flüssigen Zustand zurück.
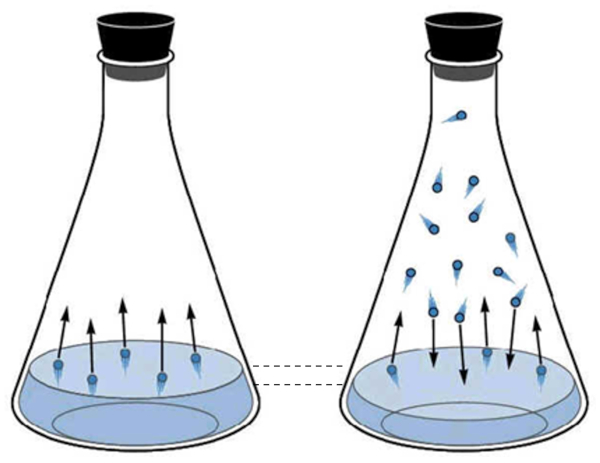
Mit zunehmender Anzahl von Molekülen im gasförmigen Zustand steigt auch die Anzahl derer, die in den flüssigen Zustand zurückkehren. Dieser Prozess setzt sich fort, bis ein Gleichgewicht zwischen den Molekülen erreicht ist, die die Flüssigkeit verlassen, und denen, die wieder aufgenommen werden. In dieser Situation wird gesagt, dass der Raum über der Flüssigkeit gesättigt ist.
ID:(1010, 0)
Menge an Wasserdampf
Konzept 
Wenn die Volumenvariation beim Phasenwechsel ($\Delta V$) von einer Flüssigkeit zu einem Gas wechselt, kann es wie folgt ausgedrückt werden:
$\Delta V = V_{\text{Gas}} - V_{\text{Flüssigkeit}}$
Da das Volumen des Gases deutlich größer ist als das der Flüssigkeit,
$V_{\text{Gas}} \gg V_{\text{Flüssigkeit}}$
können wir näherungsweise annehmen:
$\Delta V \approx V_{\text{Gas}}$
Da Wasserdampf sich ähnlich wie ein ideales Gas verhält, können wir mit den Werten von die Universelle Gas Konstante ($R_C$), der Anzahl der Mol ($n$), die Absolute Temperatur ($T$) und die Wasserdampfdruck Ungesättigte ($p_v$) sagen:
| $ p V = n R_C T $ |
Daher ist die Volumenvariation beim Phasenwechsel ($\Delta V$):
$\Delta V = \displaystyle\frac{nRT}{p_v}$
ID:(3185, 0)
Wasserdampf auf dem Boden
Modell 
Normalerweise ist der Druck des realen Wasserdampfs niedriger als das Maximum, das er der Luft widerstehen kann, bevor sie zu kondensieren beginnt. Daher wird das Konzept der relativen Luftfeuchtigkeit eingeführt.
Variablen
Berechnungen
Berechnungen
Gleichungen
Unter Verwendung der Clausius-Clapeyron-Gleichung f r den Gradienten von die Druck ($p$) in Bezug auf die Absolute Temperatur ($T$), der von der Latentwärme ($L$) und die Volumenvariation beim Phasenwechsel ($\Delta V$) abh ngt:
| $\displaystyle\frac{ dp }{ dT }=\displaystyle\frac{ L }{ \Delta V T }$ |
Im Fall des Phasen bergangs von Fl ssigkeit zu Gas k nnen wir annehmen, dass die nderung des Volumens ungef hr gleich dem Volumen des Dampfes ist. Daher k nnen wir die ideale Gasgleichung mit der Anzahl der Mol ($n$), der Volumen ($V$), die Universelle Gas Konstante ($R_C$) und die Wasserdampfdruck Ungesättigte ($p_v$) verwenden:
| $$ |
Da die Clausius-Clapeyron-Gleichung wie folgt geschrieben werden kann:
$\displaystyle\frac{dp}{dT}=\displaystyle\frac{L}{n}\displaystyle\frac{p}{R T^2}$
Wobei der Molare Latenzwärme ($l_m$) ($l_m = L/n$) der nderung der Enthalpie w hrend des Phasen bergangs h entspricht (die f r die Bildung von Wasser ben tigte Energie), erhalten wir schlie lich:
$\displaystyle\frac{dp}{dT}=l_m\displaystyle\frac{p}{RT^2}$
Wenn wir diese Gleichung zwischen die Druck gesättigtem Wasserdampf ($p_s$) und dem Druck am Punkt
$p_s=p_0e^{l_m/RT_0}e^{-l_m/RT}$
Wenn wir diesen Ausdruck mit den Daten am kritischen Punkt auswerten:
$p_{ref}=p_0e^{l_m/RT_0}$
Haben wir schlie lich:
| $ p_s = p_{ref} e^{- l_m / R_C T }$ |
(ID 3182)
Da der Interne Energiedifferenz ($dU$) gem der Gleichung von der Differential ungenau Wärme ($\delta Q$), die Druck ($p$) und die Volumenvariation ($\Delta V$) abh ngt:
| $ dU = \delta Q - p dV $ |
und der Ausdruck f r das zweite Gesetz der Thermodynamik mit die Absolute Temperatur ($T$) und die Entropievariation ($dS$) lautet:
| $ \delta Q = T dS $ |
k nnen wir daraus schlie en:
| $ dU = T dS - p dV $ |
(ID 3471)
Wenn wir die Definition von die Enthalpie ($H$) differenzieren, die von die Innere Energie ($U$), die Druck ($p$) und der Volumen ($V$) abh ngt, gem
| $ H = U + p V $ |
erhalten wir:
$dH = dU + Vdp + pdV$
unter Verwendung von der Differential Enthalpie ($dH$), der Interne Energiedifferenz ($dU$), die Pressure Variation ($dp$) und die Volumenvariation ($\Delta V$).
Durch die Differenzierung von die Innere Energie ($U$) in Bezug auf die Absolute Temperatur ($T$) und die Entropie ($S$),
| $ U = T S - p V $ |
erhalten wir:
| $ dU = T dS - p dV $ |
mit der Interne Energiedifferenz ($dU$) und die Entropievariation ($dS$).
Daraus ergibt sich schlie lich:
| $ dH = T dS + V dp $ |
(ID 3473)
(ID 3536)
Die Freie Gibbs-Energie ($G$) in Abh ngigkeit von die Enthalpie ($H$), die Entropie ($S$) und die Absolute Temperatur ($T$) wird wie folgt ausgedr ckt:
| $ G = H - T S $ |
Der Wert von der Differential der Gibbs Freien Energie ($dG$) wird unter Verwendung von der Differential Enthalpie ($dH$), die Temperaturschwankungen ($dT$) und die Entropievariation ($dS$) durch die Gleichung bestimmt:
$dG=dH-SdT-TdS$
Da der Differential Enthalpie ($dH$) in Beziehung zu der Volumen ($V$) und die Pressure Variation ($dp$) steht wie folgt:
| $ dH = T dS + V dp $ |
Folgt daraus, dass der Differential Enthalpie ($dH$), die Entropievariation ($dS$) und die Pressure Variation ($dp$) auf folgende Weise miteinander verbunden sind:
| $ dG =- S dT + V dp $ |
(ID 3541)
Die Beziehung zwischen die Relative Luftfeuchtigkeit ($RH$) mit die Konzentration von Wasserdampfmolekülen ($c_v$) und ERROR:4952,0 wird wie folgt ausgedr ckt:
| $ RH =\displaystyle\frac{ c_v }{ c_s }$ |
und durch die Beziehung zwischen die Druck ($p$) mit die Molare Konzentration ($c_m$), die Absolute Temperatur ($T$) und die Universelle Gas Konstante ($R_C$) erhalten wir:
| $ p = c_m R_C T $ |
Dies gilt f r den Wasserdampfdruck, wobei:
$p_v = c_v R T$
und den ges ttigten Wasserdampfdruck:
$p_s = c_s R T$
was zur folgenden Gleichung f hrt:
| $ RH =\displaystyle\frac{ p_v }{ p_s }$ |
(ID 4478)
Wenn die Druck ($p$) sich wie ein ideales Gas verh lt und der Volumen ($V$), der Anzahl der Mol ($n$), die Absolute Temperatur ($T$) und die Universelle Gas Konstante ($R_C$) erf llt, f hrt die ideale Gasgleichung:
| $ p V = n R_C T $ |
und die Definition von die Molare Konzentration ($c_m$):
| $ c_m \equiv\displaystyle\frac{ n }{ V }$ |
zu folgender Beziehung:
| $ p = c_m R_C T $ |
(ID 4479)
(ID 9634)
(ID 9639)
Mit dem Clausius-Clapeyron-Gesetz, das von die Pressure Variation ($dp$), die Temperaturschwankungen ($dT$), der Latentwärme ($L$), die Volumenvariation beim Phasenwechsel ($\Delta V$) und die Absolute Temperatur ($T$) abh ngt und wie folgt ausgedr ckt wird:
| $\displaystyle\frac{ dp }{ dT }=\displaystyle\frac{ L }{ \Delta V T }$ |
und der Definition von der Molare Latenzwärme ($l_m$), bei der der Latentwärme ($L$) wie folgt mit die Molmasse ($M_m$) zusammenh ngt:
| $ l_m \equiv\displaystyle\frac{ L }{ M_m }$ |
und der Variation des Molvolumens während des Phasenwechsels ($\Delta v_m$), bei der die Volumenvariation beim Phasenwechsel ($\Delta V$) wie folgt mit die Molmasse ($M_m$) zusammenh ngt:
| $\Delta v_m =\displaystyle\frac{ \Delta V }{ M_m }$ |
erhalten wir:
| $\displaystyle\frac{ dp }{ dT }=\displaystyle\frac{ l_m }{ \Delta v_m T }$ |
(ID 12822)
Wenn der Differential der Gibbs Freien Energie ($dG$) konstant ist, bedeutet dies, dass f r die Pressure Variation ($dp$) und die Temperaturschwankungen ($dT$) die Werte von die Entropie ($S$) und der Volumen ($V$) in Phase 1
$dG = -S_1dT+V_1dp$
und die Entropie ($S$) und der Volumen ($V$) in Phase 2
$dG = -S_2dT+V_2dp$
ergibt sich
$\displaystyle\frac{dp}{dT}=\displaystyle\frac{S_2-S_1}{V_2-V_1}$
Die nderung in die Entropie ($S$) zwischen beiden Phasen entspricht der Latentwärme ($L$) geteilt durch die Absolute Temperatur ($T$):
$S_2 - S_1 =\displaystyle\frac{ L }{ T }$
Also, mit der Definition von die Volumenvariation beim Phasenwechsel ($\Delta V$)
$\Delta V \equiv V_2 - V_1$
erhalten wir
| $\displaystyle\frac{ dp }{ dT }=\displaystyle\frac{ L }{ \Delta V T }$ |
(ID 12824)
Beispiele
(ID 15211)
Die gasf rmige Phase, die in unserem Fall Wasserdampf entspricht, ist die Phase, in der Atome sich relativ frei bewegen k nnen.

In dieser Phase gibt es nur minimale Wechselwirkungen, die das Verhalten der Atome beeinflussen k nnen, ohne sie signifikant einzuschr nken.
(ID 15142)
Die fl ssige Phase, die in unserem Fall Wasser entspricht, ist die Phase, in der Atome sich relativ frei bewegen k nnen, dabei jedoch ihre Einheit beibehalten und sich der Form anpassen, die sie umgibt.

In dieser Phase wird keine spezifische Struktur beobachtet.
(ID 15140)
Die feste Phase, die in unserem Fall dem Eis entspricht, ist die Phase, in der sich Atome nicht relativ bewegen k nnen und nur um ihren Gleichgewichtspunkt schwingen k nnen.

In dieser Phase kann man eine Struktur beobachten, die oft kristallin und daher regelm ig ist.
(ID 15141)
Eines der relevantesten Phasendiagramme f r unseren Planeten ist das des Wassers. Dieses Diagramm zeigt die drei klassischen Phasen: fest, fl ssig und gasf rmig, sowie verschiedene Phasen mit unterschiedlichen kristallinen Strukturen des Eises.

Der bedeutende Unterschied zu anderen Materialien besteht darin, dass im Druckbereich von 611 Pa bis 209,9 MPa die feste Phase ein gr eres Volumen einnimmt als die fl ssige Phase. Diese Eigenschaft spiegelt sich im Phasendiagramm als eine negative Neigung entlang der Grenzlinie zwischen der festen Phase (hexagonales Eis) und der fl ssigen Phase (Wasser) wider.
(ID 836)
Die Messung der Verdampfungsenthalpie erfolgt durch Erw rmen einer Probe, wodurch sie verdampft, w hrend gleichzeitig die zugef hrte W rme gemessen wird. Anschlie end wird der erzeugte Dampf gek hlt und kondensiert, wobei die Masse gemessen wird, die urspr nglich verdampft ist.

Auf diese Weise k nnen wir die f r die Verdampfung einer gegebenen Masse ben tigte Energie absch tzen, die in ERROR:5238,0 gemessen wird, und zwar in Joule pro Kilogramm (J/kg) oder Joule pro Mol (J/mol).
(ID 1662)
Die gasf rmige Phase des Wassers entspricht dem, was als Wasserdampf bekannt ist. Diese entsteht, wenn Wassermolek le gen gend kinetische Energie erhalten, um aus der fl ssigen Phase zu entweichen und sich im Raum ber der Fl ssigkeit zu bewegen. Periodisch kollidieren die Molek le im gasf rmigen Zustand erneut mit der Oberfl che der Fl ssigkeit und werden erfasst, kehren in den fl ssigen Zustand zur ck.

Mit zunehmender Anzahl von Molek len im gasf rmigen Zustand steigt auch die Anzahl derer, die in den fl ssigen Zustand zur ckkehren. Dieser Prozess setzt sich fort, bis ein Gleichgewicht zwischen den Molek len erreicht ist, die die Fl ssigkeit verlassen, und denen, die wieder aufgenommen werden. In dieser Situation wird gesagt, dass der Raum ber der Fl ssigkeit ges ttigt ist.
(ID 1010)
(ID 15231)
Wenn die Volumenvariation beim Phasenwechsel ($\Delta V$) von einer Fl ssigkeit zu einem Gas wechselt, kann es wie folgt ausgedr ckt werden:
$\Delta V = V_{\text{Gas}} - V_{\text{Fl ssigkeit}}$
Da das Volumen des Gases deutlich gr er ist als das der Fl ssigkeit,
$V_{\text{Gas}} \gg V_{\text{Fl ssigkeit}}$
k nnen wir n herungsweise annehmen:
$\Delta V \approx V_{\text{Gas}}$
Da Wasserdampf sich hnlich wie ein ideales Gas verh lt, k nnen wir mit den Werten von die Universelle Gas Konstante ($R_C$), der Anzahl der Mol ($n$), die Absolute Temperatur ($T$) und die Wasserdampfdruck Ungesättigte ($p_v$) sagen:
| $ p V = n R_C T $ |
Daher ist die Volumenvariation beim Phasenwechsel ($\Delta V$):
$\Delta V = \displaystyle\frac{nRT}{p_v}$
(ID 3185)
ID:(377, 0)
