Temperatur und Hitze
Storyboard 
Die Temperatur des Bodens hängt von seiner Wärmekapazität und dem Wärmeaustausch zur oder von der Bodenoberfläche ab. Die Wärmekapazität wird durch die Zusammensetzung des Bodens und die Menge an Wasser und Wasserdampf, die er enthält, beeinflusst.
ID:(2052, 0)
Mikroskopische Wärme
Beschreibung 
Wärme ist nichts anderes als Energie auf mikroskopischer Ebene.
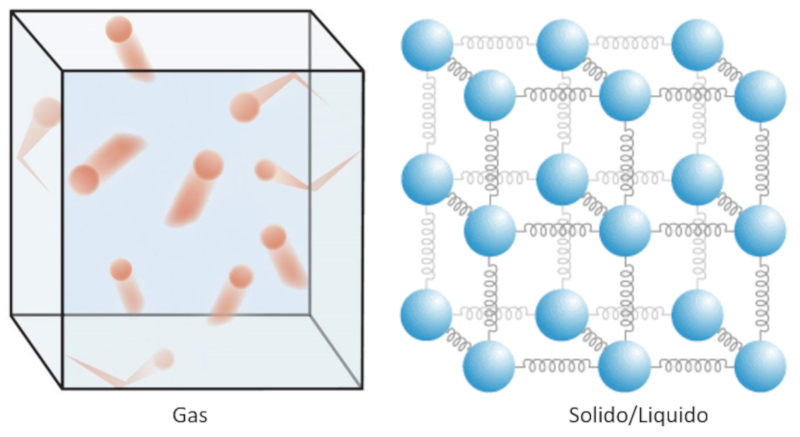
Im Falle eines Gases entspricht dies hauptsächlich der kinetischen Energie seiner Moleküle.In Flüssigkeiten und Feststoffen müssen wir die Anziehungskraft zwischen den Atomen berücksichtigen, wobei auch die potenzielle Energie eine wichtige Rolle spielt. In diesen Fällen entspricht die Wärme der Energie, die die Partikel besitzen und mit der sie um den Gleichgewichtspunkt herum schwingen, der durch die umgebenden Partikel definiert wird.
ID:(118, 0)
Temperatur
Beschreibung 
Die Temperatur ist der Parameter, den wir verwenden, um die Wärmeenergie in einem Objekt zu messen. Da Wärmeenergie niemals negativ sein kann, ist es unerlässlich, mit der Kelvin-Skala zu arbeiten, bei der der Nullpunkt dem vollständigen Fehlen dieser Energie entspricht.
ID:(1009, 0)
Wärme
Beschreibung 
Hitze wird mit Elementen wie Feuer in Verbindung gebracht, die dazu führen, dass die Wassertemperatur steigt. Durch Erwärmung entsteht Bewegung, was darauf hinweist, dass Hitze mit mechanischer Energie verbunden ist. Selbst der Griff eines Topfes erhitzt sich, und unser Körper ist in der Lage, diese Temperatur wahrzunehmen. Darüber hinaus emittiert Feuer Strahlung, die Gegenstände erwärmt, die ihr ausgesetzt sind.
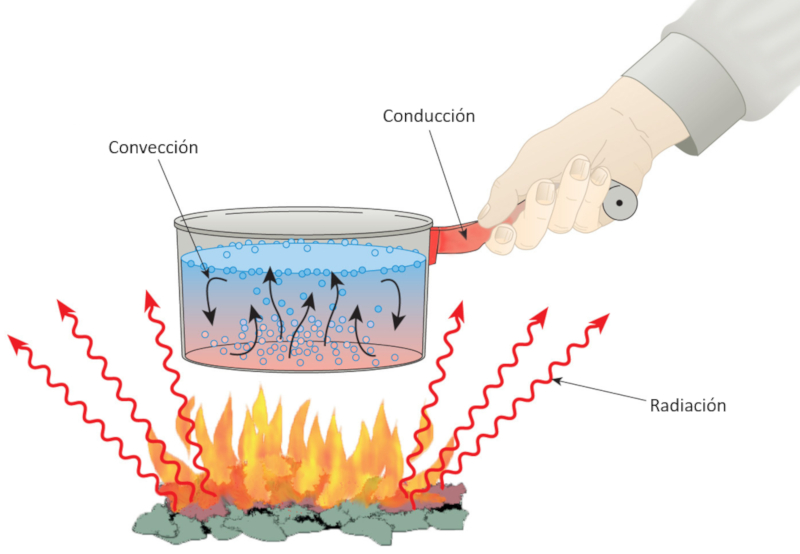
Daraus können wir ableiten, dass wir durch die Übertragung von Wärme die Temperatur eines Objekts erhöhen können und dass die Erzeugung von Bewegung mit Energie verbunden ist.
ID:(585, 0)
Temperatur und Hitze
Modell 
Die Temperatur des Bodens hängt von seiner Wärmekapazität und dem Wärmeaustausch zur oder von der Bodenoberfläche ab. Die Wärmekapazität wird durch die Zusammensetzung des Bodens und die Menge an Wasser und Wasserdampf, die er enthält, beeinflusst.
Variablen
Berechnungen
Berechnungen
Gleichungen
(ID 3197)
(ID 4381)
Die Der Flüssigkeit oder dem Feststoff zugeführte Wärme ($\Delta Q$) ist in Beziehung zu die Temperaturschwankungen ($\Delta T$) und die Wärmekapazität ($C$) wie folgt:
| $ \Delta Q = C \Delta T $ |
Wobei die Wärmekapazität ($C$) durch der Spezifische Wärme ($c$) und die Masse ($M$) gem folgender Beziehung ersetzt werden kann:
| $ c =\displaystyle\frac{ C }{ M }$ |
Daher erhalten wir:
| $ \Delta Q = M c \Delta T$ |
(ID 11112)
(ID 12772)
Mit die i-te Masse des Systems ($M_i$) und der Spezifische Wärme der i-ten Masse ($c_i$) k nnen Sie der Spezifische Wärme ($c$) f r den Boden mithilfe der folgenden Gleichung berechnen:
| $ c =\displaystyle\frac{ \displaystyle\sum_i c_i M_i }{ \displaystyle\sum_i M_i }$ |
Zus tzlich k nnen Sie mit den Variablen die Sandtrockenmasse ($M_a$), die Trockene Schlammmasse in der Probe ($M_i$), die Masa seca de arcilla en la muestra ($M_c$) und die Wassermasse im Boden ($M_w$) zusammen mit der Spezifische Wärme von Sand ($c_a$), der Spezifische Wärme von Schluff ($c_i$), der Spezifische Wärme von Ton ($c_c$) und der Spezifische Wärme von Wasser ($c_w$) die spezifische W rme (
$c$
) mit der folgenden Formel erhalten:
$c=\displaystyle\frac{M_ac_a+M_ic_i+M_cc_c+M_wc_w}{M_a+M_i+M_c+M_w}$
Unter Verwendung der folgenden Gleichungen:
| $ g_a =\displaystyle\frac{ M_a }{ M_s }$ |
| $ g_i =\displaystyle\frac{ M_i }{ M_s }$ |
| $ g_c =\displaystyle\frac{ M_c }{ M_s }$ |
| $ g_a + g_i + g_c = 1$ |
und
| $ \theta_w =\displaystyle\frac{ M_w }{ M_s }$ |
Wird der Spezifische Wärme ($c$) dann mit der folgenden Gleichung vereinfacht:
| $ c = \displaystyle\frac{ g_a c_a + g_i c_i + g_c c_c + \theta_w c_w }{1+ \theta_w }$ |
(ID 15125)
Die Menge von die Wärmekapazität ($C$) in einem System von die i-te Masse des Systems ($M_i$) mit der Spezifische Wärme der i-ten Masse ($c_i$) kann wie folgt berechnet werden:
$C = \displaystyle\sum_i c_i M_i$
wobei die Summe der Massen wie folgt erhalten wird:
$M = \displaystyle\sum_i M_i$
Daher k nnen wir mit Hilfe der Gleichung
| $ c =\displaystyle\frac{ C }{ M }$ |
die Wärmekapazität ($C$) wie folgt berechnen:
| $ c =\displaystyle\frac{ \displaystyle\sum_i c_i M_i }{ \displaystyle\sum_i M_i }$ |
(ID 15126)
Beispiele
(ID 15210)
W rme ist nichts anderes als Energie auf mikroskopischer Ebene.

Im Falle eines Gases entspricht dies haupts chlich der kinetischen Energie seiner Molek le.In Fl ssigkeiten und Feststoffen m ssen wir die Anziehungskraft zwischen den Atomen ber cksichtigen, wobei auch die potenzielle Energie eine wichtige Rolle spielt. In diesen F llen entspricht die W rme der Energie, die die Partikel besitzen und mit der sie um den Gleichgewichtspunkt herum schwingen, der durch die umgebenden Partikel definiert wird.
(ID 118)
Die Temperatur ist der Parameter, den wir verwenden, um die W rmeenergie in einem Objekt zu messen. Da W rmeenergie niemals negativ sein kann, ist es unerl sslich, mit der Kelvin-Skala zu arbeiten, bei der der Nullpunkt dem vollst ndigen Fehlen dieser Energie entspricht.
(ID 1009)
Hitze wird mit Elementen wie Feuer in Verbindung gebracht, die dazu f hren, dass die Wassertemperatur steigt. Durch Erw rmung entsteht Bewegung, was darauf hinweist, dass Hitze mit mechanischer Energie verbunden ist. Selbst der Griff eines Topfes erhitzt sich, und unser K rper ist in der Lage, diese Temperatur wahrzunehmen. Dar ber hinaus emittiert Feuer Strahlung, die Gegenst nde erw rmt, die ihr ausgesetzt sind.

Daraus k nnen wir ableiten, dass wir durch die bertragung von W rme die Temperatur eines Objekts erh hen k nnen und dass die Erzeugung von Bewegung mit Energie verbunden ist.
(ID 585)
(ID 15228)
ID:(2052, 0)
