Storyboard

Die Feuchtigkeit im Boden hängt von seiner Temperatur ab, daher ist es wichtig, diese Verteilung zu berechnen. Diese Beziehung wird durch den Wärmeaustausch mit der Bodenoberfläche bestimmt.

>Modell

ID:(2054, 0)

Konzept

>Top

ID:(15207, 0)

Konzept

>Top

Im Fall eines Festkörpers und ähnlich für eine Flüssigkeit können wir das System als eine Struktur von Atomen beschreiben, die durch etwas verbunden sind, das sich wie eine Feder verhält. Wenn beide Enden Temperaturen von eine Temperaturunterschied im Leiter ($\Delta T_0$) haben, wobei die Innenoberflächentemperatur ($T_{is}$) und die Äußere Oberflächentemperatur ($T_{es}$) sind:

Der Temperaturunterschied bedeutet, dass die Atome an den Enden unterschiedlich schwingen; Atome in der Zone mit hoher Temperatur haben eine größere Amplitude in ihren Schwingungen im Vergleich zu den Atomen in der Zone mit niedriger Temperatur.

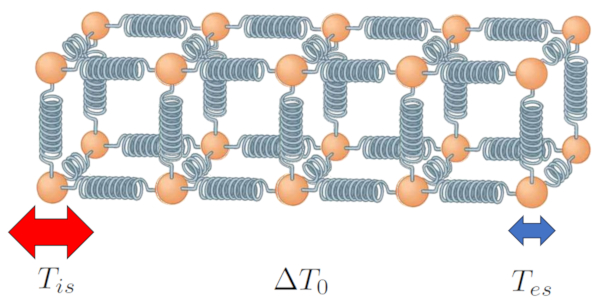
Diese Differenz führt jedoch allmählich dazu, dass die gesamte Kette so schwingt, dass die Amplitude am Wegesrand von den höchsten Werten, wo die Temperatur ebenfalls höher ist, bis zu den niedrigsten Werten in der Zone mit niedrigerer Temperatur variiert.

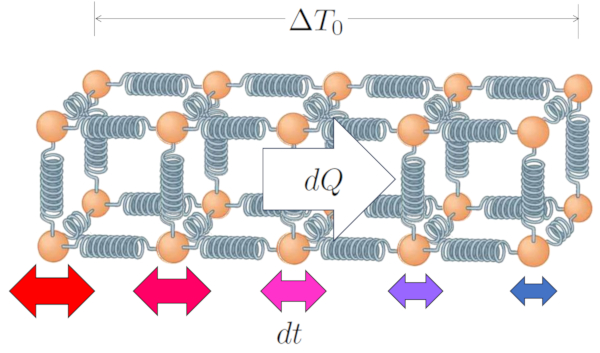
Auf diese Weise führt die Temperaturunterschied im Leiter ($\Delta T_0$) zu eine Variation des Wärme ($dQ$) in eine Zeitvariation ($dt$).

ID:(15234, 0)

Konzept

>Top

Einer der Schlüsselfaktoren, der bestimmt, wie viel Wärme durch einen Feststoff oder eine Flüssigkeit geleitet werden kann, ist sein Querschnitt, das heißt, die Anzahl der verfügbaren Atomketten. Je mehr dieser Ketten wir haben, desto größer ist unsere Wärmetransportkapazität.

Jedoch kann die Länge dieser Ketten kontraproduktiv sein. Wenn die Federkette länger wird, nimmt unsere Fähigkeit zur Wärmeübertragung ab, da mehr Atome ihre Schwingungsamplituden anpassen müssen.

Wenn wir dies mit die Abschnitt ($S$) und der Leitungslänge ($L$) darstellen, nimmt das Diagramm folgende Form an:

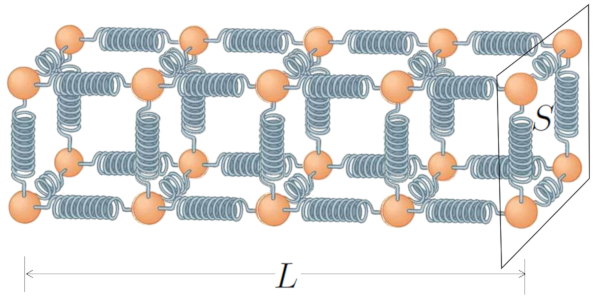
Schließlich erklärt die Fähigkeit des Mediums und des Materials zur Wärmeübertragung, die durch die Koeffizienten der Interner Übertragungskoeffizient ($\alpha_i$) und der Externer Transmissionskoeffizient ($\alpha_e$) und die Wärmeleitfähigkeit ($\lambda$) beschrieben wird, wie die Wärme in Reaktion auf die Temperaturdifferenz ($\Delta T$) übertragen wird, das durch die Differenz zwischen die Innentemperatur ($T_i$) und die Außentemperatur ($T_e$) erzeugt wird:

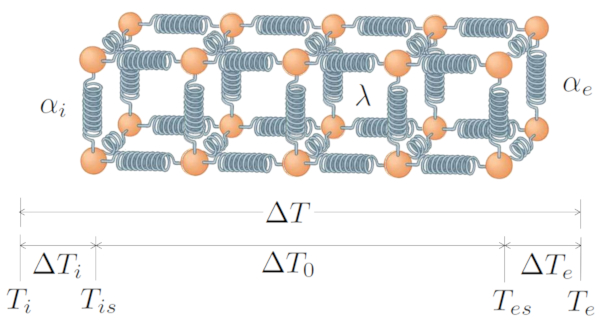
Dies wird wie folgt berechnet:

ID:(15235, 0)

Konzept

>Top

Auf diese Weise wird eine Beziehung hergestellt, die es uns ermöglicht, die Variation des Wärme ($dQ$) basierend auf die Zeitvariation ($dt$), die Abschnitt ($S$), der Leitungslänge ($L$), die Temperaturunterschied im Leiter ($\Delta T_0$) und die Wärmeleitfähigkeit ($\lambda$) zu berechnen:



Mathematisch kann dies wie folgt ausgedrückt werden:

ID:(15236, 0)

Konzept

>Top

Der Haupttreiber für den Wärmeübergang von einem Medium auf einen Leiter ist der Temperaturunterschied. In dem Medium die Innentemperatur ($T_i$) haben die Teilchen mehr Energie, und wenn sie mit denen im Leiter bei eine Innenoberflächentemperatur ($T_{is}$) kollidieren, neigen sie dazu, die Energie des Letzteren zu erhöhen. Diese Interaktion kann wie folgt dargestellt werden:

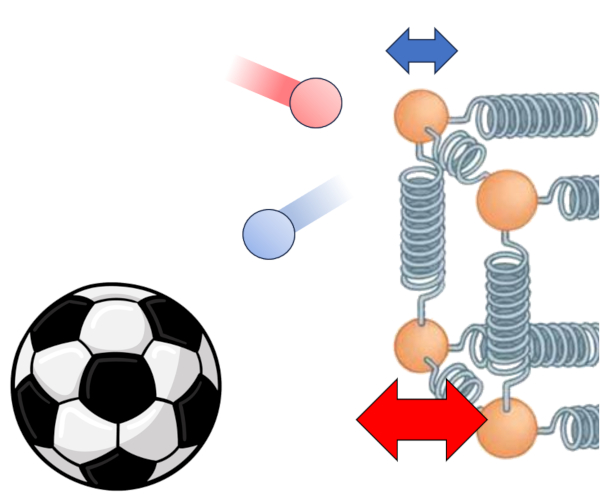
Neben der Temperatur selbst hängt der Wärmefluss von die Temperaturunterschied an der internen Schnittstelle ($\Delta T_i$) ab:

Ein weiterer entscheidender Faktor ist die Anzahl der Atome, deren Oszillationsamplitude erhöht werden kann, was von die Abschnitt ($S$) abhängt. Schließlich müssen wir auch die Eigenschaften der Oberfläche berücksichtigen, die durch der Interner Übertragungskoeffizient ($\alpha_i$) beschrieben werden. Dies entspricht dem Verhältnis zwischen übertragener Wärme, Oberfläche, Temperaturunterschied und verstrichener Zeit:

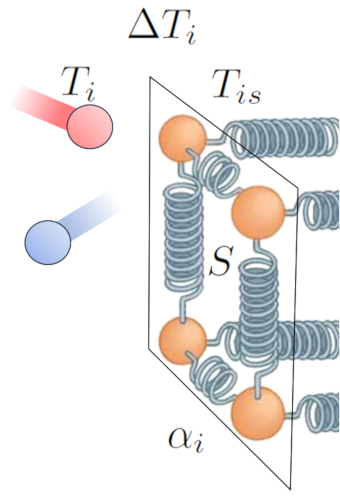
ID:(15237, 0)

Konzept

>Top

Auf diese Weise etablieren wir eine Beziehung, die es uns ermöglicht, die Variation des Wärme ($dQ$) basierend auf die Zeitvariation ($dt$), die Abschnitt ($S$), die Temperaturunterschied an der internen Schnittstelle ($\Delta T_i$) und der Interner Übertragungskoeffizient ($\alpha_i$) zu berechnen:

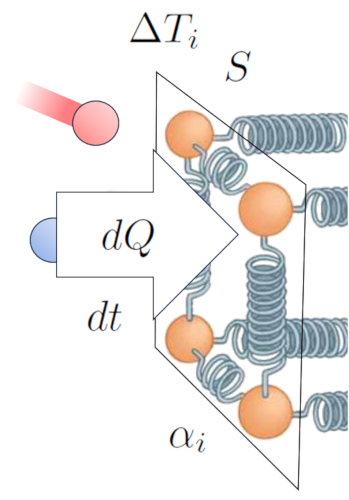
Dies kann mathematisch wie folgt ausgedrückt werden:

ID:(15238, 0)

Konzept

>Top

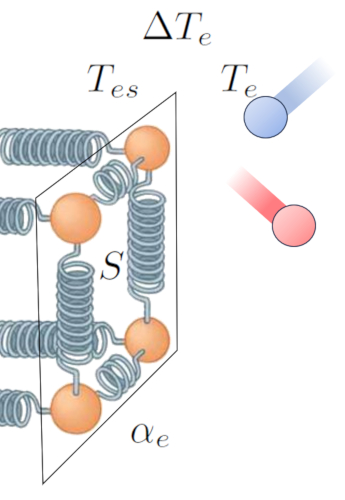
Der Haupttreiber für den Wärmeübergang von einem Leiter zu einem Medium ist der Temperaturunterschied. Wenn die Äußere Oberflächentemperatur ($T_{es}$), haben die Teilchen mehr Energie und schwingen mit einer größeren Amplitude, wenn sie mit den Atomen und Molekülen des Mediums bei eine Außentemperatur ($T_e$) interagieren. Dies führt dazu, dass die Energie dieser letzten erhöht wird. Diese Interaktion kann wie folgt dargestellt werden:

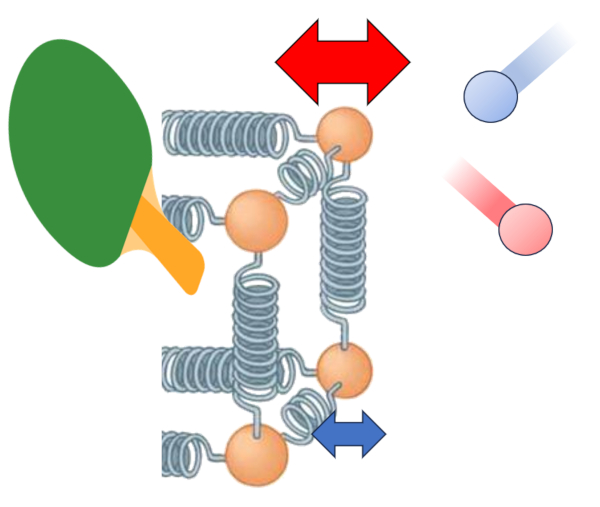
Neben der Temperatur hängt der Wärmefluss von die Temperaturunterschied an der externen Schnittstelle ($\Delta T_e$) ab.

Ein weiterer entscheidender Faktor ist die Anzahl der Atome, deren Oszillationsamplitude erhöht werden kann, was von die Abschnitt ($S$) abhängt. Abschließend müssen wir die Oberflächeneigenschaften berücksichtigen, die durch der Externer Transmissionskoeffizient ($\alpha_e$) repräsentiert werden. Dies entspricht dem Verhältnis zwischen übertragener Wärme, Oberfläche, Temperaturunterschied und verstrichener Zeit:

ID:(15239, 0)

Konzept

>Top

Auf diese Weise etablieren wir eine Beziehung, die es uns ermöglicht, die Variation des Wärme ($dQ$) basierend auf die Zeitvariation ($dt$), die Abschnitt ($S$), die Temperaturunterschied an der externen Schnittstelle ($\Delta T_e$) und der Externer Transmissionskoeffizient ($\alpha_e$) zu berechnen:

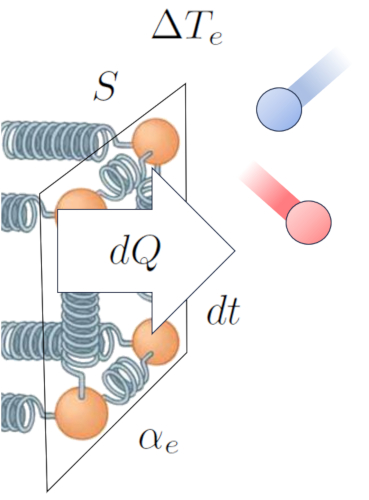
Dies kann mathematisch wie folgt ausgedrückt werden:

ID:(15240, 0)

Konzept

>Top

Wärmeübertragungs- und Leitungsmodelle legen nahe, dass es möglich ist, eine Beziehung zu entwickeln, die alle drei Mechanismen zusammenfasst. Diese Gleichung sollte die Variation des Wärme ($dQ$), die Zeitvariation ($dt$), die Temperaturdifferenz ($\Delta T$), die Abschnitt ($S$) und der Gesamttransportkoeffizient (mehrere Medien, zwei Schnittstellen) ($k$) berücksichtigen:

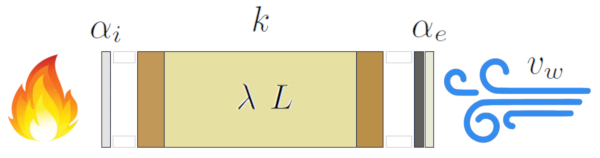
Mathematisch kann dies wie folgt ausgedrückt werden:

ID:(15241, 0)

Konzept

>Top

Einer der Effekte bei der Wärmeübertragung von einem Leiter auf ein externes Medium ist, dass die Zone in der Nähe der Grenzfläche beginnen kann, sich zu erwärmen und eine Störungszone in der Übertragung zu schaffen. Dies verringert die Effizienz der Übertragung und neigt dazu, eine isolierende Schicht zu erzeugen, die den Energiefluss reduziert.

Allerdings kann dieser Effekt in Anwesenheit von Wind variieren, da der Wind diese Schicht aus hochtemperierten Atomen und Molekülen entfernen kann, was die Wärmeübertragung effizienter macht. Dies bedeutet, dass der Durchgangskoeffizient ($\alpha$) von die Mittlere Geschwindigkeit ($v_m$) abhängt:

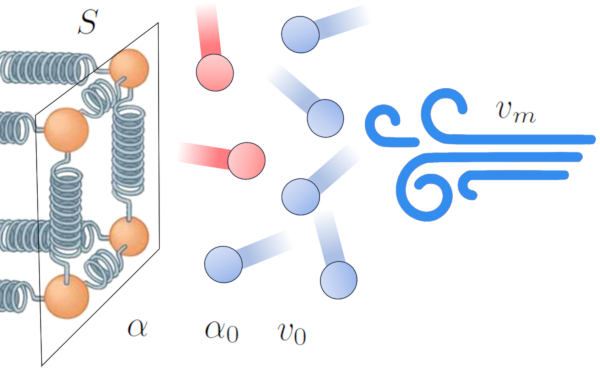
In diesem Fall modellieren wir die Beziehung basierend auf Übertragungskoeffizient ohne Geschwindigkeit ($\alpha_0$) und einem Referenzfaktor von der Medienreferenzgeschwindigkeit ($v_0$).

Die mathematische Beziehung, die dies beschreibt, gilt für ein Gas mit der Transmissionskoeffizient in Gasen, abhängig von der Geschwindigkeit ($\alpha_{gv}$), die Mittlere Geschwindigkeit ($v_m$), der Transmissionskoeffizient in Gasen, unabhängig von der Geschwindigkeit ($\alpha_{g0}$) und der Transmissionskoeffizient Gasgeschwindigkeitsfaktor ($v_{g0}$):

und für eine Flüssigkeit mit der Durchgangskoeffizient abhängig von der Geschwindigkeit ($\alpha_{wv}$), die Mittlere Geschwindigkeit ($v_m$), der Durchgangskoeffizient unabhängig von der Geschwindigkeit ($\alpha_{w0}$) und der Factor Velocidad del Coefiente de Transmisión ($v_{w0}$):

Dies erklärt, wie der Wind die Effizienz der Wärmeübertragung zwischen einem Leiter und einem externen Medium beeinflussen kann.

ID:(3620, 0)

Konzept

>Top

Ausgewählter Parameter

Berechnungen

ID:(15229, 0)

Gleichung

>Top, >Modell

Im Fall eines Festkörpers und ähnlich für eine Flüssigkeit können wir das System als eine Struktur von Atomen beschreiben, die durch etwas verbunden sind, das sich wie eine Feder verhält. Wenn beide Enden Temperaturen von eine Temperaturunterschied im Leiter ($\Delta T_0$) haben, wobei die Innenoberflächentemperatur ($T_{is}$) und die Äußere Oberflächentemperatur ($T_{es}$) sind:

$ \Delta T_0 = T_{is} - T_{es} $

Bedingungen

Variablen

Beziehung

ID:(15120, 0)

Gleichung

>Top, >Modell

Die Temperaturdifferenz ($\Delta T$) wird durch Subtraktion von die Außentemperatur ($T_e$) und die Innentemperatur ($T_i$) berechnet, was wie folgt ausgedrückt wird:

$ \Delta T = T_i - T_e $

Bedingungen

Variablen

Beziehung

ID:(15116, 0)

Gleichung

>Top, >Modell

Auf diese Weise wird eine Beziehung hergestellt, die es uns ermöglicht, die Variation des Wärme ($dQ$) basierend auf die Zeitvariation ($dt$), die Abschnitt ($S$), der Leitungslänge ($L$), die Temperaturunterschied im Leiter ($\Delta T_0$) und die Wärmeleitfähigkeit ($\lambda$) zu berechnen:

$\displaystyle\frac{ dQ }{ dt } = \displaystyle\frac{ S }{ L } \lambda \Delta T_0 $

Bedingungen

Variablen

Beziehung

ID:(7712, 0)

Gleichung

>Top, >Modell

Die Temperaturunterschied an der internen Schnittstelle ($\Delta T_i$) wird berechnet, indem die Innenoberflächentemperatur ($T_{is}$) von die Innentemperatur ($T_i$) subtrahiert wird:

$ \Delta T_i = T_i - T_{is} $

Bedingungen

Variablen

Beziehung

ID:(15117, 0)

Konzept

>Top

Auf diese Weise etablieren wir eine Beziehung, die es uns ermöglicht, die Variation des Wärme ($dQ$) basierend auf die Zeitvariation ($dt$), die Abschnitt ($S$), die Temperaturunterschied an der internen Schnittstelle ($\Delta T_i$) und der Interner Übertragungskoeffizient ($\alpha_i$) zu berechnen:

$\displaystyle\frac{ dQ }{ dt } = S \alpha_i \Delta T_i $

Bedingungen

Variablen

Beziehung

ID:(15113, 0)

Gleichung

>Top, >Modell

Die Temperaturunterschied an der externen Schnittstelle ($\Delta T_e$) wird berechnet, indem die Äußere Oberflächentemperatur ($T_{es}$) von die Außentemperatur ($T_e$) subtrahiert wird:

$ \Delta T_e = T_{es} - T_e $

Bedingungen

Variablen

Beziehung

ID:(15118, 0)

Gleichung

>Top, >Modell

Auf diese Weise etablieren wir eine Beziehung, die es uns ermöglicht, die Variation des Wärme ($dQ$) basierend auf die Zeitvariation ($dt$), die Abschnitt ($S$), die Temperaturunterschied an der externen Schnittstelle ($\Delta T_e$) und der Externer Transmissionskoeffizient ($\alpha_e$) zu berechnen:

$\displaystyle\frac{ dQ }{ dt } = S \alpha_e \Delta T_e $

Bedingungen

Variablen

Beziehung

ID:(15114, 0)

Gleichung

>Top, >Modell

Auf diese Weise etablieren wir eine Beziehung, die es uns ermöglicht, die Variation des Wärme ($dQ$) als Funktion von die Zeitvariation ($dt$), die Abschnitt ($S$), der Gesamttransportkoeffizient (mehrere Medien, zwei Schnittstellen) ($k$) und die Temperaturdifferenz ($\Delta T$) zu berechnen:

$\displaystyle\frac{ dQ }{ dt } = k S \Delta T $

Bedingungen

Variablen

$S$

Abschnitt

$m^2$

$k$

Gesamttransportkoeffizient (mehrere Medien, zwei Schnittstellen)

$J/m s K$

$\Delta T$

Temperaturdifferenz

$K$

$dQ$

Variation des Wärme

$J$

$dt$

Zeitvariation

$s$

Beziehung

Entwicklung

Mit die Temperaturunterschied an der internen Schnittstelle ($\Delta T_i$), die Temperaturunterschied im Leiter ($\Delta T_0$), die Temperaturunterschied an der externen Schnittstelle ($\Delta T_e$) und die Temperaturdifferenz ($\Delta T$) erhalten wir

$ \Delta T = \Delta T_i + \Delta T_0 + \Delta T_e $

die mit die Variation des Wärme ($dQ$), die Zeitvariation ($dt$), die Abschnitt ($S$)

$\displaystyle\frac{ dQ }{ dt } = S \alpha_i \Delta T_i $

$\displaystyle\frac{ dQ }{ dt } = S \alpha_e \Delta T_e $

und mit die Wärmeleitfähigkeit ($\lambda$) und der Leitungslänge ($L$)

$\displaystyle\frac{ dQ }{ dt } = \displaystyle\frac{ S }{ L } \lambda \Delta T_0 $

und

$\displaystyle\frac{1}{ k }=\displaystyle\frac{1}{ \alpha_i }+\displaystyle\frac{1}{ \alpha_e }+\displaystyle\frac{ L }{ \lambda }$

als

$\Delta T = \Delta T_i + \Delta T_0 + \Delta T_e = \displaystyle\frac{1}{S} \frac{dQ}{dt} \left(\displaystyle\frac{1}{\alpha_i} + \displaystyle\frac{1}{\alpha_e} + \displaystyle\frac{L}{\lambda}\right) = \displaystyle\frac{1}{Sk} \displaystyle\frac{dQ}{dt}$

resultiert in

$\displaystyle\frac{ dQ }{ dt } = k S \Delta T $

ID:(7716, 0)

Gleichung

>Top, >Modell

Im Prozess des Wärmetransports sinkt die Temperatur allmählich vom System mit der höchsten Temperatur (intern) zum System mit der niedrigsten Temperatur (extern). In diesem Prozess nimmt sie zuerst von der durchschnittlichen internen Temperatur auf die Temperaturunterschied an der internen Schnittstelle ($\Delta T_i$) ab, dann auf die Temperaturunterschied im Leiter ($\Delta T_0$) und schließlich auf die Temperaturunterschied an der externen Schnittstelle ($\Delta T_e$). Die Summe dieser drei Veränderungen entspricht dem Gesamtabfall, nämlich die Temperaturdifferenz ($\Delta T$), wie unten gezeigt:

$ \Delta T = \Delta T_i + \Delta T_0 + \Delta T_e $

Bedingungen

Variablen

Beziehung

ID:(15115, 0)

Gleichung

>Top, >Modell

Der Wert von der Koeffizient Gesamttransportation (die Hälfte, zwei Schnittstellen) ($k$) in der Transportgleichung wird unter Verwendung von der Externer Transmissionskoeffizient ($\alpha_e$), der Interner Übertragungskoeffizient ($\alpha_i$), die Wärmeleitfähigkeit ($\lambda$) und der Leitungslänge ($L$) wie folgt bestimmt:

$\displaystyle\frac{1}{ k }=\displaystyle\frac{1}{ \alpha_i }+\displaystyle\frac{1}{ \alpha_e }+\displaystyle\frac{ L }{ \lambda }$

Bedingungen

Variablen

$\alpha_e$

Externer Transmissionskoeffizient

$W/m^2K$

$\alpha_i$

Interner Übertragungskoeffizient

$W/m^2K$

$k$

Koeffizient Gesamttransportation (die Hälfte, zwei Schnittstellen)

$J/m s K$

$L$

Leitungslänge

$m$

$\lambda$

Wärmeleitfähigkeit

$J/m s K$

Beziehung

Entwicklung

Mit die Temperaturunterschied an der internen Schnittstelle ($\Delta T_i$), die Temperaturunterschied im Leiter ($\Delta T_0$), die Temperaturunterschied an der externen Schnittstelle ($\Delta T_e$) und die Temperaturdifferenz ($\Delta T$) erhalten wir

$ \Delta T = \Delta T_i + \Delta T_0 + \Delta T_e $

die mit die Variation des Wärme ($dQ$), die Zeitvariation ($dt$), die Abschnitt ($S$)

$\displaystyle\frac{ dQ }{ dt } = S \alpha_i \Delta T_i $

$\displaystyle\frac{ dQ }{ dt } = S \alpha_e \Delta T_e $

und mit die Wärmeleitfähigkeit ($\lambda$) und der Leitungslänge ($L$)

$\displaystyle\frac{ dQ }{ dt } = \displaystyle\frac{ S }{ L } \lambda \Delta T_0 $

als

$\Delta T_i + \Delta T_0 + \Delta T_e = \displaystyle\frac{1}{S} \displaystyle\frac{dQ}{dt} \left(\displaystyle\frac{1}{\alpha_i} + \displaystyle\frac{1}{\alpha_e} + \displaystyle\frac{L}{\lambda}\right)$

definieren können wir einen kombinierten Koeffizienten als

$\displaystyle\frac{1}{ k }=\displaystyle\frac{1}{ \alpha_i }+\displaystyle\frac{1}{ \alpha_e }+\displaystyle\frac{ L }{ \lambda }$

ID:(3486, 0)

Gleichung

>Top, >Modell

Die Innenoberflächentemperatur ($T_{is}$) entspricht nicht der Temperatur des Mediums selbst, die die Innentemperatur ($T_i$) beträgt. Diese Temperatur kann anhand von die Temperaturdifferenz ($\Delta T$), der Gesamttransportkoeffizient (mehrere Medien, zwei Schnittstellen) ($k$) und der Interner Übertragungskoeffizient ($\alpha_i$) mit folgender Formel berechnet werden:

$ T_{is} = T_i - \displaystyle\frac{ k }{ \alpha_i } \Delta T $

Bedingungen

Variablen

Beziehung

Entwicklung

Mit die Variation des Wärme ($dQ$), die Zeitvariation ($dt$), die Abschnitt ($S$), die Temperaturdifferenz ($\Delta T$) und der Gesamttransportkoeffizient (mehrere Medien, zwei Schnittstellen) ($k$) erhalten wir

$\displaystyle\frac{ dQ }{ dt } = k S \Delta T $

was mit der Interner Übertragungskoeffizient ($\alpha_i$) und die Temperaturunterschied an der internen Schnittstelle ($\Delta T_i$)

$\displaystyle\frac{ dQ }{ dt } = S \alpha_i \Delta T_i $

ergibt

$k\Delta T = \alpha_i \Delta T_i$

und mit die Innentemperatur ($T_i$) und die Innenoberflächentemperatur ($T_{is}$) und

$ \Delta T_i = T_i - T_{is} $

resultiert in

$ T_{is} = T_i - \displaystyle\frac{ k }{ \alpha_i } \Delta T $

ID:(15121, 0)

Gleichung

>Top, >Modell

Die Äußere Oberflächentemperatur ($T_{es}$) entspricht nicht der Temperatur des Mediums, die die Außentemperatur ($T_e$) beträgt. Diese Temperatur kann anhand von die Temperaturdifferenz ($\Delta T$), der Gesamttransportkoeffizient (mehrere Medien, zwei Schnittstellen) ($k$) und der Externer Transmissionskoeffizient ($\alpha_e$) mit folgender Formel berechnet werden:

$ T_{es} = T_e + \displaystyle\frac{ k }{ \alpha_e } \Delta T $

Bedingungen

Variablen

Beziehung

Entwicklung

Mit die Variation des Wärme ($dQ$), die Zeitvariation ($dt$), die Abschnitt ($S$), die Temperaturdifferenz ($\Delta T$) und der Gesamttransportkoeffizient (mehrere Medien, zwei Schnittstellen) ($k$) erhalten wir

$\displaystyle\frac{ dQ }{ dt } = k S \Delta T $

was, mit der Externer Transmissionskoeffizient ($\alpha_e$) und die Temperaturunterschied an der externen Schnittstelle ($\Delta T_e$)

$\displaystyle\frac{ dQ }{ dt } = S \alpha_e \Delta T_e $

zu

$k\Delta T = \alpha_e \Delta T_e$

und mit die Außentemperatur ($T_e$) und die Äußere Oberflächentemperatur ($T_{es}$) und

$ \Delta T_e = T_{es} - T_e $

zu

$ T_{es} = T_e + \displaystyle\frac{ k }{ \alpha_e } \Delta T $

führt.

ID:(15122, 0)

Gleichung

>Top, >Modell

Die Konstante $k$ in der Transportgleichung wird wie folgt berechnet:

$ \displaystyle\frac{1}{ k }=\displaystyle\frac{1}{ \alpha }+\displaystyle\frac{ L }{ \lambda }$

Bedingungen

Variablen

$\alpha$

Durchgangskoeffizient

$W/m^2K$

$k$

Koeffizient Gesamttransportation (eine halbe Schnittstellen)

$J/m s K$

$L$

Leitungslänge

$m$

$\lambda$

Wärmeleitfähigkeit

$J/m s K$

Beziehung

ID:(3619, 0)

Gleichung

>Top, >Modell

Die Transportkonstante $k$ durch Medien mit Wärmeleitfähigkeit $\lambda_i$ und Dicke $L_i$, jeweils mit Übertragungskoeffizienten an beiden Grenzflächen $\alpha_1$ und $\alpha_2$, wird wie folgt berechnet:

$\displaystyle\frac{1}{k}=\displaystyle\frac{1}{\alpha_1}+\displaystyle\frac{1}{\alpha_2}+\sum_i\displaystyle\frac{L_i}{\lambda_i}$

Bedingungen

Variablen

$\alpha_1$

Durchgangskoeffizient Schnittstelle 1

$W/m^2K$

$\alpha_2$

Durchgangskoeffizient Schnittstelle 2

$W/m^2K$

$L_i$

Elementlänge i

$m$

$k$

Gesamttransportkoeffizient (mehrere Medien, zwei Schnittstellen)

$J/m s K$

$\lambda_i$

Wärmeleitelement i

$J/m s K$

Beziehung

ID:(7730, 0)

Gleichung

>Top, >Modell

Falls ein Medium sich mit einer Konstanten von eine Mittlere Geschwindigkeit ($v_m$) bewegt und der Transmissionskoeffizient in Gasen, abhängig von der Geschwindigkeit ($\alpha_{gv}$) gleich ist

$ \alpha_{gv} = \alpha_{g0} \left(1+\displaystyle\frac{ v_m }{ v_{g0} }\right)$

Bedingungen

Variablen

$v_m$

Mittlere Geschwindigkeit

$m/s$

$v_{g0}$

Transmissionskoeffizient Gasgeschwindigkeitsfaktor

$m/s$

$\alpha_g$

Transmissionskoeffizient in Gasen, abhängig von der Geschwindigkeit

$W/m^2K$

$\alpha_{g0}$

Transmissionskoeffizient in Gasen, unabhängig von der Geschwindigkeit

$W/m^2K$

Beziehung

wobei der Transmissionskoeffizient in Gasen, unabhängig von der Geschwindigkeit ($\alpha_{g0}$) den Fall repräsentiert, in dem das Medium sich nicht bewegt, und der Transmissionskoeffizient Gasgeschwindigkeitsfaktor ($v_{g0}$) die Referenzgeschwindigkeit ist.

Die thermische Transferkonstante für das Material im Fall eines ruhenden Gases beträgt $5,6 J/m^2sK$, während die Referenzgeschwindigkeit $1,41 m/s$ beträgt.

ID:(7715, 0)

Gleichung

>Top, >Modell

Wenn ein Medium mit einer Konstanten von der Durchgangskoeffizient abhängig von der Geschwindigkeit ($\alpha_{wv}$) bewegt wird und die Mittlere Geschwindigkeit ($v_m$) gleich

$ \alpha_{wv} = \alpha_{w0} \left(1+\sqrt{\displaystyle\frac{ v_m }{ v_{w0} }}\right)$

Bedingungen

Variablen

$\alpha_l$

Durchgangskoeffizient abhängig von der Geschwindigkeit

$W/m^2K$

$\alpha_{l0}$

Durchgangskoeffizient unabhängig von der Geschwindigkeit

$W/m^2K$

$v_{l0}$

Factor Velocidad del Coefiente de Transmisión

0.0278

$m/s$

$v_m$

Mittlere Geschwindigkeit

$m/s$

Beziehung

ist, wobei der Durchgangskoeffizient unabhängig von der Geschwindigkeit ($\alpha_{w0}$) den Fall repräsentiert, in dem sich das Medium nicht bewegt, und der Factor Velocidad del Coefiente de Transmisión ($v_{w0}$) die Referenzgeschwindigkeit ist.

Die thermische Übertragungskonstante des Materials für den Fall einer ruhenden Flüssigkeit beträgt $340 J/m^2sK$, während die Referenzgeschwindigkeit $0,0278 m/s$ beträgt.

ID:(7714, 0)

Gleichung

>Top, >Modell

Die Modellierung der thermischen Leitfähigkeit in einem porösen Medium wie Boden stellt eine Herausforderung dar. In dieser Studie wurden Analysen an einer breiten Palette von Proben durchgeführt und ein numerisches Modell entwickelt, um die Wärmeleitfähigkeit in trockenem Boden ($\lambda_b$) basierend auf den Bodenstrukturen vorherzusagen [1].

Die Beziehung von die Wärmeleitfähigkeit in trockenem Boden ($\lambda_b$) wurde anhand von die Wärmeleitfähigkeit in Sand ($\lambda_a$), die Wärmeleitfähigkeit im Schlick ($\lambda_i$), die Wärmeleitfähigkeit in Ton ($\lambda_c$) und die Massenanteil von Sand in der Probe ($g_a$), die Massenanteil von Schluff in der Probe ($g_i$), die Massenanteil von Ton in der Probe ($g_c$) mit der folgenden Formel ermittelt:

$ \lambda_b = \lambda_a g_a + \lambda_i g_i + \lambda_c g_c $

Bedingungen

Variablen

Beziehung

[1] "Physical principles and calculation methods of moisture and heat transfer in cable trenches." (Physikalische Prinzipien und Berechnungsmethoden für Feuchtigkeits- und Wärmeübertragung in Kabelgräben), Brakelmann, H., etz-Report 19, 93p. (1984), Berlin; Offenbach.

ID:(15130, 0)

Gleichung

>Top, >Modell

Die Modellierung der thermischen Leitfähigkeit in einem porösen Medium wie Boden stellt eine Herausforderung dar. In dieser Studie wurden Analysen an einer breiten Palette von Proben durchgeführt und ein numerisches Modell entwickelt, um die Wärmeleitfähigkeit in trockenem Boden ($\lambda_b$) basierend auf den Bodenstrukturen vorherzusagen [1].

Die Beziehung von die Wärmeleitfähigkeit in trockenem Boden ($\lambda_b$) wurde anhand von die Wärmeleitfähigkeit in Sand ($\lambda_a$), die Wärmeleitfähigkeit im Schlick ($\lambda_i$), die Wärmeleitfähigkeit in Ton ($\lambda_c$) und die Massenanteil von Sand in der Probe ($g_a$), die Massenanteil von Schluff in der Probe ($g_i$), die Massenanteil von Ton in der Probe ($g_c$) mit der folgenden Formel ermittelt:

$ \lambda = \lambda_w^{\Phi} \lambda_b^{1-\Phi} e^{-\beta \Phi (1-\theta_S)^2}$

Bedingungen

Variablen

Beziehung

[1] "Physical principles and calculation methods of moisture and heat transfer in cable trenches." (Physikalische Prinzipien und Berechnungsmethoden für Feuchtigkeits- und Wärmeübertragung in Kabelgräben), Brakelmann, H., etz-Report 19, 93p. (1984), Berlin; Offenbach.

ID:(15131, 0)