Benützer:
Temperaturentwicklung
Storyboard 
Die Temperatur im Boden entwickelt sich in Abhängigkeit von der Oberflächentemperatur und der mittleren Temperatur in der Tiefe. Die Wärmeleitfähigkeit und die spezifische Wärmekapazität des Bodens bestimmen die Tiefe, auf der die mittlere Temperatur erreicht wird.
ID:(2051, 0)
Temperaturentwicklung
Modell
Die Temperatur im Boden entwickelt sich in Abhängigkeit von der Oberflächentemperatur und der mittleren Temperatur in der Tiefe. Die Wärmeleitfähigkeit und die spezifische Wärmekapazität des Bodens bestimmen die Tiefe, auf der die mittlere Temperatur erreicht wird.
Variablen
Berechnungen
zu 
,
dann die Variable auswählen: 
zu 
Berechnungen
Variable
Gegeben
Berechnen
Ziel :
Gleichung
Zu verwenden
Gleichungen
Da die Wärme transportiert ($dQ$) eine Funktion von der Leitungslänge ($L$), die Abschnitt ($S$), die Zeitvariation ($dt$), die Temperaturunterschied im Leiter ($\Delta T_0$) und die Wärmeleitfähigkeit ($\lambda$) gem folgender Gleichung ist:
| $ q = \displaystyle\frac{ \lambda }{ L } \Delta T_0 $ |
Mit der Gleichung f r die Wärmestromrate ($q$) definiert als:
| $ q \equiv \displaystyle\frac{1}{ S }\displaystyle\frac{ dQ }{ dt }$ |
Im infinitesimalen Fall, in dem der Leitungslänge ($L$) zu eine Zurückgelegte Strecke ($dz$) wird und die Temperaturunterschied im Leiter ($\Delta T_0$) zu die Temperaturschwankungen ($dT$) wird, vereinfacht sich die Gleichung zu:
| $ q = - \lambda \displaystyle\frac{dT}{dz}$ |
(ID 15132)
Die Menge von die Wärme transportiert ($dQ$) durch eine Zurückgelegte Strecke ($dz$) kann mithilfe von die Wärmestromrate ($q$) und die Zeitvariation ($dt$) mit die Abschnitt ($S$) durch folgende Gleichung berechnet werden:
$dQ = -\displaystyle\frac{\partial}{\partial z}(q S dt) dz$
Da die Wärmestromrate ($q$) mit die Temperaturschwankungen ($dT$) und die Wärmeleitfähigkeit ($\lambda$) definiert ist als:
| $ q = - \lambda \displaystyle\frac{dT}{dz}$ |
Daher gilt:
$dQ = \displaystyle\frac{\partial}{\partial z}(\lambda \displaystyle\frac{\partial T}{\partial z}) S dz dt$
Andererseits k nnen wir die Der Flüssigkeit oder dem Feststoff zugeführte Wärme ($\Delta Q$) mit die Masse ($M$), der Spezifische Wärme ($c$) und die Temperaturschwankungen ($\Delta T$) durch die Gleichung verkn pfen:
| $ \Delta Q = M c \Delta T$ |
In diesem Fall, mit die Volumenvariation ($\Delta V$), wird die Gleichung zu:
$dQ=\rho dV c dT = \rho c S dz dT$
Und schlie lich erhalten wir:
| $ \displaystyle\frac{\partial T}{\partial t}=\displaystyle\frac{\lambda}{\rho c}\displaystyle\frac{\partial^2 T}{\partial z^2}$ |
(ID 15134)
Wie die Wärmestromrate ($q$) zusammen mit die Wärmeleitfähigkeit ($\lambda$), die Bodentemperatur ($T$) und die Tiefe ($z$) ergibt
| $ q = - \lambda \displaystyle\frac{dT}{dz}$ |
F r die L sung von die Bodentemperatur ($T$) mit die Tiefe ($z$) und der Zeit ($t$) verwenden wir die Durchschnittliche Umwelttemperatur ($T_m$), die Jährliche Temperaturschwankung im Boden ($\Delta T_s$), die Zeit Phasenverschiebung ($t_0$), die Durchschnittliche Variationstiefe ($d_m$) und die Durchschnittliche Variationstiefe ($\omega_m$):
| $ T = T_m - \displaystyle\frac{1}{2} \Delta T_s e^{- z / d_m }\cos( \omega_m ( t - t_0 ) - z / d_m )$ |
Dies wird an der Oberfl che ($z=0$) und ohne Phasenverschiebung ($t_0=0$) erhalten:
| $ q = \displaystyle\frac{ \lambda \Delta T_s }{2 d_m }(\cos \omega_m ( t - t_0 ) - \sin \omega_m ( t - t_0 ))$ |
(ID 15138)
Die Wärmestromrate ($q$) als Funktion von die Wärmeleitfähigkeit ($\lambda$), die Jährliche Temperaturschwankung im Boden ($\Delta T_s$), die Durchschnittliche Variationstiefe ($d_m$), die Durchschnittliche Variationstiefe ($\omega_m$), der Zeit ($t$) und die Zeit Phasenverschiebung ($t_0$) wird durch folgende Gleichung dargestellt:
| $ q = \displaystyle\frac{ \lambda \Delta T_s }{2 d_m }(\cos \omega_m ( t - t_0 ) - \sin \omega_m ( t - t_0 ))$ |
Diese repr sentiert den Gesamtfluss, der durch den Bereich ber dem Boden und dem Boden selbst flie t. Im ersten Fall betr gt der Fluss aufgrund der Temperaturdifferenz zwischen der Umgebung und der Bodenoberfl che der Durchgangskoeffizient ($\alpha$). F r die Situation, in der der Zeit ($t$) gleich die Zeit Phasenverschiebung ($t_0$) ist, kann der Fluss im Bereich ber dem Boden wie folgt beschrieben werden:
$\alpha \left(\displaystyle\frac{\Delta T_m}{2}-\displaystyle\frac{\Delta T_s}{2}\right) = \displaystyle\frac{\lambda \Delta T_s}{2 d_m}$
Wenn wir nach die Jährliche Temperaturschwankung im Boden ($\Delta T_s$) aufl sen, erhalten wir:
| $ \Delta T_s = \displaystyle\frac{ \alpha }{ \alpha + \lambda / d_m } \Delta T_m $ |
(ID 15139)
Beispiele
(ID 15208)
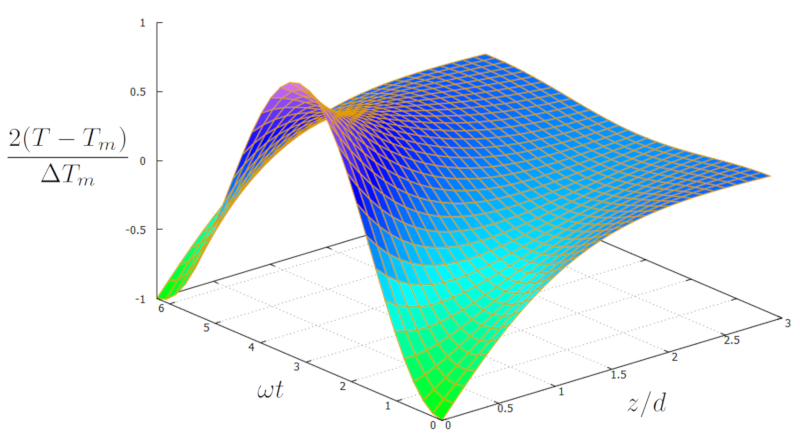
Wenn wir die L sung f r die Bodentemperatur ($T$) ber die Tiefe ($z$) und der Zeit ($t$) mithilfe von die Durchschnittliche Umwelttemperatur ($T_m$), die Jährliche Temperaturschwankung im Boden ($\Delta T_s$), die Zeit Phasenverschiebung ($t_0$), die Durchschnittliche Variationstiefe ($d_m$) und die Durchschnittliche Variationstiefe ($\omega_m$) grafisch darstellen, ergibt sich:
| $ T = T_m - \displaystyle\frac{1}{2} \Delta T_s e^{- z / d_m }\cos( \omega_m ( t - t_0 ) - z / d_m )$ |
Dies ergibt eine Kurve, die an der Oberfl che ($z=0$) das Maximum des Sommers und das Minimum des Winters in der Temperatur zeigt. Die Temperatur konvergiert dann mit zunehmender Tiefe zur Durchschnittstemperatur und bleibt konstant. Dar ber hinaus gibt es einen Tr gheitseffekt im System:
(ID 15137)
(ID 15230)
ID:(2051, 0)