Vapeur d'eau au sol
Storyboard 
Variables
Calculs
Calculs
Équations
En utilisant l' quation de Clausius-Clapeyron pour le gradient de a pression ($p$) par rapport a température absolue ($T$), qui d pend de le chaleur latente ($L$) et a variation de volume en changement de phase ($\Delta V$) :
Dans le cas du changement de phase de liquide gaz, on peut supposer que le changement de volume est approximativement gal au volume du gaz. Par cons quent, nous pouvons utiliser l' quation des gaz parfaits avec le nombre de taupes ($n$), le volume ($V$), a constante du gaz universel ($R_C$) et a pression de vapeur d'eau non saturée ($p_v$) :
Comme l' quation de Clausius-Clapeyron peut tre crite comme suit :
$\displaystyle\frac{dp}{dT}=\displaystyle\frac{L}{n}\displaystyle\frac{p}{R T^2}$
O Le chaleur latente molaire ($l_m$) ($l_m = L/n$) correspond au changement d'enthalpie lors du changement de phase h (l' nergie n cessaire pour former de l'eau), nous obtenons finalement :
$\displaystyle\frac{dp}{dT}=l_m\displaystyle\frac{p}{RT^2}$
Si nous int grons cette quation entre a pression de vapeur d'eau saturée ($p_s$) et la pression au point
$p_s=p_0e^{l_m/RT_0}e^{-l_m/RT}$
Si nous valuons cette expression avec les donn es au point critique :
$p_{ref}=p_0e^{l_m/RT_0}$
Nous avons finalement :
Comme le différentiel d'énergie interne ($dU$) d pend de le différence de chaleur inexacte ($\delta Q$), a pression ($p$) et a variation de volume ($\Delta V$) selon l' quation :
et l'expression de la deuxi me loi de la thermodynamique avec a température absolue ($T$) et a variation d'entropie ($dS$) est la suivante :
nous pouvons en conclure que :
Si l'on diff rencie la d finition de a enthalpie ($H$), qui d pend de a énergie interne ($U$), a pression ($p$) et le volume ($V$), selon
on obtient :
$dH = dU + Vdp + pdV$
en utilisant le différentiel d'enthalpie ($dH$), le différentiel d'énergie interne ($dU$), a variation de pression ($dp$) et a variation de volume ($\Delta V$).
En diff renciant a énergie interne ($U$) par rapport a température absolue ($T$) et a entropie ($S$),
on obtient :
avec le différentiel d'énergie interne ($dU$) et a variation d'entropie ($dS$).
Finalement, on conclut que :
A énergie libre de Gibbs ($G$) en fonction de a enthalpie ($H$), a entropie ($S$), et a température absolue ($T$) s'exprime comme suit :
La valeur de le différentiel d'énergie libre de Gibbs ($dG$) est d termin e en utilisant le différentiel d'enthalpie ($dH$), a variation de température ($dT$), et a variation d'entropie ($dS$) travers l' quation :
$dG=dH-SdT-TdS$
Puisque le différentiel d'enthalpie ($dH$) est li le volume ($V$) et a variation de pression ($dp$) comme suit :
Il s'ensuit que le différentiel d'enthalpie ($dH$), a variation d'entropie ($dS$), et a variation de pression ($dp$) sont interconnect s de la mani re suivante :
La relation entre a humidité relative ($RH$) avec a concentration de molécules de vapeur d'eau ($c_v$) et ERROR:4952,0 est exprim e comme suit :
et en reliant a pression ($p$) avec a concentration molaire ($c_m$), a température absolue ($T$), et a constante du gaz universel ($R_C$), nous obtenons :
Cela s'applique la pression de vapeur d'eau, o :
$p_v = c_v R T$
et la pression de vapeur satur e de l'eau :
$p_s = c_s R T$
ce qui donne l' quation suivante :
Quand a pression ($p$) se comporte comme un gaz id al, en satisfaisant le volume ($V$), le nombre de taupes ($n$), a température absolue ($T$) et a constante du gaz universel ($R_C$), l' quation des gaz id aux :
et la d finition de a concentration molaire ($c_m$) :
conduisent la relation suivante :
Avec la loi de Clausius-Clapeyron, qui d pend de a variation de pression ($dp$), a variation de température ($dT$), le chaleur latente ($L$), a variation de volume en changement de phase ($\Delta V$) et a température absolue ($T$), exprim e comme suit :
et la d finition de le chaleur latente molaire ($l_m$), o le chaleur latente ($L$) est li a masse molaire ($M_m$) comme suit :
et le variation du volume molaire lors du changement de phase ($\Delta v_m$), o a variation de volume en changement de phase ($\Delta V$) est li a masse molaire ($M_m$) comme suit :
nous obtenons :
Si le différentiel d'énergie libre de Gibbs ($dG$) est constant, cela signifie que pour a variation de pression ($dp$) et a variation de température ($dT$), les valeurs de a entropie ($S$) et le volume ($V$) en phase 1
$dG = -S_1dT+V_1dp$
et a entropie ($S$) et le volume ($V$) en phase 2
$dG = -S_2dT+V_2dp$
donnent
$\displaystyle\frac{dp}{dT}=\displaystyle\frac{S_2-S_1}{V_2-V_1}$
La variation de a entropie ($S$) entre les deux phases correspond le chaleur latente ($L$) divis par a température absolue ($T$) :
$S_2 - S_1 =\displaystyle\frac{ L }{ T }$
Ainsi, avec la d finition de a variation de volume en changement de phase ($\Delta V$)
$\Delta V \equiv V_2 - V_1$
nous obtenons
Exemples
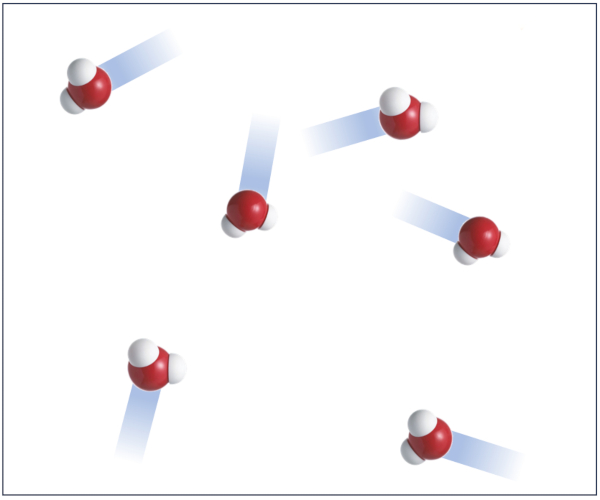
La phase gazeuse, qui dans notre cas correspond la vapeur d'eau, est la phase dans laquelle les atomes peuvent se d placer relativement librement.
Dans cette phase, il n'y a qu'une interaction minimale qui peut influencer le comportement des atomes sans les confiner de mani re significative.
La phase liquide, qui dans notre cas correspond l'eau, est la phase dans laquelle les atomes peuvent se d placer relativement librement tout en maintenant leur unit et en s'adaptant la forme qui les contient.
Dans cette phase, aucune structure sp cifique n'est observ e.
La phase solide, qui dans notre cas correspond la glace, est la phase dans laquelle les atomes ne peuvent pas se d placer relativement et ne peuvent que osciller autour de leur point d' quilibre.
Dans cette phase, on peut observer une structure qui est souvent cristalline et donc r guli re.
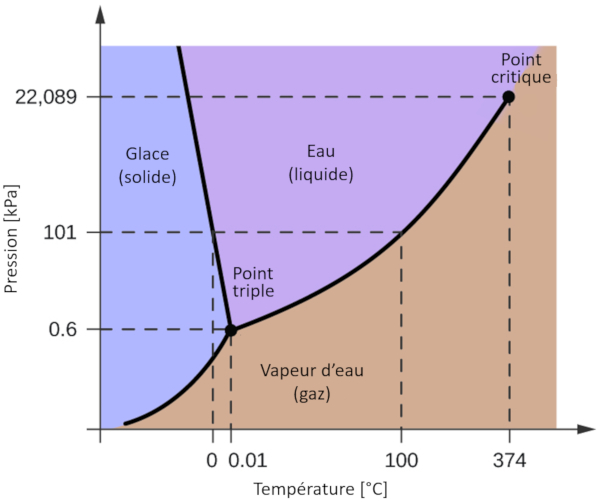
L'un des diagrammes de phase les plus pertinents pour notre plan te est celui de l'eau. Ce diagramme pr sente les trois phases classiques : solide, liquide et gazeuse, ainsi que plusieurs phases avec diff rentes structures cristallines de la glace.
La caract ristique la plus notable par rapport d'autres mat riaux est que, dans une plage de pression allant de 611 Pa 209,9 MPa, la phase solide occupe un volume plus important que la phase liquide. Cette particularit se refl te dans le diagramme de phase sous la forme d'une pente n gative le long de la ligne de s paration entre la phase solide (glace hexagonale) et la phase liquide (eau).
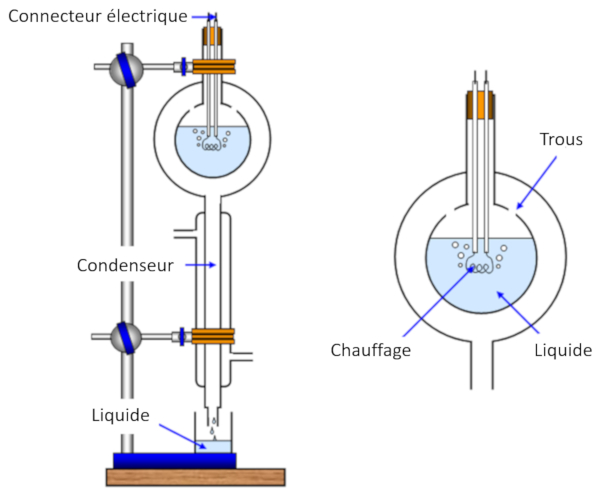
La mesure de la chaleur de vaporisation s'effectue en chauffant un chantillon, provoquant ainsi son vaporation, tout en mesurant simultan ment la chaleur fournie l' chantillon. Ensuite, la vapeur est refroidie et condens e, et la masse originellement vapor e est mesur e.
De cette mani re, nous pouvons estimer l' nergie n cessaire pour vaporiser une masse donn e, ce qui correspond ERROR:5238,0 mesur en joules par kilogramme (J/kg) ou joules par mole (J/mol).
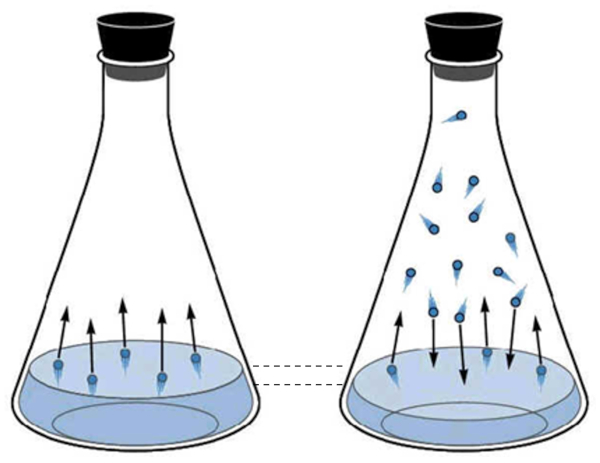
La phase gazeuse de l'eau correspond ce que l'on appelle la vapeur d'eau. Elle se forme lorsque les mol cules d'eau acqui rent suffisamment d' nergie cin tique pour s' chapper de la phase liquide et commencer se d placer dans l'espace au-dessus du liquide. P riodiquement, les mol cules l' tat gazeux entrent de nouveau en collision avec la surface liquide et sont captur es, revenant l' tat liquide.
mesure que le nombre de mol cules l' tat gazeux augmente, le nombre de mol cules qui reviennent l' tat liquide augmente galement. Ce processus se poursuit jusqu' ce qu'un quilibre soit atteint entre les mol cules quittant le liquide et celles qui sont r absorb es. Dans cette situation, on dit que l'espace au-dessus du liquide est satur .
Le différentiel d'énergie interne ($dU$) est toujours gal la quantit de le différence de chaleur inexacte ($\delta Q$) fournie au syst me (positif) moins la quantit de le différentiel de travail inexact ($\delta W$) r alis e par le syst me (n gatif) :
En analogie avec la d finition du travail $dW$ en m canique :
qui est d fini en fonction de la force $F$ et de la distance parcourue $dx$, en thermodynamique, on travaille avec l'expression du travail en fonction de la pression $p$ et de la variation de volume $dV$ :
Le différence de chaleur inexacte ($\delta Q$) est gal a température absolue ($T$) fois a variation d'entropie ($dS$)xa0:
La d pendance de le différentiel d'énergie interne ($dU$) sur a pression ($p$) et a variation de volume ($\Delta V$), en plus de a température absolue ($T$) et a variation d'entropie ($dS$) , est donn par :
A enthalpie ($H$) est d fini comme la somme de a énergie interne ($U$) et de l' nergie de formation. Cette derni re correspond au travail effectu lors de la formation, qui est gal $pV$ avec a pression ($p$) et le volume ($V$). Par cons quent, nous avons :
La d pendance de le différentiel d'enthalpie ($dH$) sur a température absolue ($T$) et a variation d'entropie ($dS$), en plus de le volume ($V$) et a variation de pression ($dp$) , est donn par:
La d pendance de ERROR:5402 sur a entropie ($S$) et a variation de température ($dT$), en plus de le volume ($V$) et a variation de pression ($dp$) , est donn par:
La loi Clausius-Clapeyron tablit une relation entre a variation de pression ($dp$) et a variation de température ($dT$) avec le chaleur latente ($L$), a température absolue ($T$) et ERROR:5239 < /var> comme suitxa0:
L' quation de Clausius-Clapeyron tablit une relation entre a variation de pression ($dp$) et a variation de température ($dT$) avec a température absolue ($T$), le chaleur latente molaire ($l_m$) et ERROR:9868 < /var> comme suitxa0:
Lorsque a variation de volume en changement de phase ($\Delta V$) change de phase, passant d'un liquide un gaz, cela peut tre exprim comme suit :
$\Delta V = V_{\text{gaz}} - V_{\text{liquide}}$
tant donn que le volume du gaz est nettement sup rieur celui du liquide,
$V_{\text{gaz}} \gg V_{\text{liquide}}$
nous pouvons approximativement crire :
$\Delta V \approx V_{\text{gaz}}$
Comme la vapeur d'eau se comporte de mani re similaire un gaz id al, nous pouvons affirmer qu'avec les valeurs de a constante du gaz universel ($R_C$), le nombre de taupes ($n$), a température absolue ($T$) et a pression de vapeur d'eau non saturée ($p_v$) :
ainsi, a variation de volume en changement de phase ($\Delta V$) est :
$\Delta V = \displaystyle\frac{nRT}{p_v}$
A pression de vapeur d'eau saturée ($p_s$) peut tre calcul l'aide de a pression de référence ($p_{ref}$), a constante du gaz universel ($R_C$), a température absolue ($T$) et le chaleur latente molaire ($l_m$) selon le formule suivante :
A pression ($p$) peut tre calcul partir de a concentration molaire ($c_m$) en utilisant a température absolue ($T$) et a constante du gaz universel ($R_C$) de la mani re suivante :
A humidité relative ($RH$) peut tre exprim en termes de a pression de vapeur d'eau non saturée ($p_v$) et a pression de vapeur d'eau saturée ($p_s$) comme suitxa0:
ID:(377, 0)