Absorción de Agua en Granos
Storyboard 
El vapor de agua interactúa con la superficie de los granos del suelo, formando capas de agua en su superficie. El grado de cobertura depende de la presión del vapor de agua presente.
ID:(374, 0)
Absorción de Agua en Granos
Storyboard 
El vapor de agua interactúa con la superficie de los granos del suelo, formando capas de agua en su superficie. El grado de cobertura depende de la presión del vapor de agua presente.
Variables
Cálculos
Cálculos
Ecuaciones
La presión ($p$), el volumen ($V$), la temperatura absoluta ($T$) y el número de moles ($n$) est n vinculados a trav s de las siguientes leyes f sicas:
• La ley de Boyle
• La ley de Charles
• La ley de Gay-Lussac
• La ley de Avogadro
Estas leyes pueden ser expresadas de manera m s general como:
$\displaystyle\frac{pV}{nT}=cte$
Esta relaci n general establece que el producto de la presi n y el volumen dividido por el n mero de moles y la temperatura se mantiene constante:
La fracción de cobertura de agua ($\theta$) se puede calcular utilizando la constante de Langmuir ($\alpha$) y la concentración molar ($c_m$) mediante la ecuaci n:
Si sustituimos la concentración molar ($c_m$) por la presión de vapor de agua no saturado ($p_v$) utilizando la constante universal de los gases ($R_C$) y la temperatura absoluta ($T$) a trav s de la ecuaci n:
se observa que la constante de Langmuir ($\alpha$) puede ser reemplazado por la constante de Langmuir ($\alpha_p$) utilizando la ecuaci n:
lo que resulta en:
La relaci n entre la humedad relativa ($RH$) con la concentración de moleculas de vapor de agua ($c_v$) y ERROR:4952,0 se expresa como:
y relacionando la presión ($p$) con la concentración molar ($c_m$), la temperatura absoluta ($T$) y la constante universal de los gases ($R_C$) se obtiene:
Esto se aplica a la presi n de vapor de agua, donde:
$p_v = c_v R T$
y a la presi n saturada de vapor de agua:
$p_s = c_s R T$
Lo que resulta en la siguiente ecuaci n:
$ \theta =\displaystyle\frac{ \alpha c_m }{1+ \alpha c_m }$
theta = alpha * c_m /(1+ alpha * c_m )
With the occupied spaces la concentración segunda componente ($[P]$), the empty spaces associated with la concentración primera componente ($[S]$), and the occupied spaces associated with la concentración componente reaccionada ($[SP]$) and el cociente de concentración ($K$):
If la fracción de cobertura de agua ($\theta$) represents the fraction of surface occupied by molecules:
$[SP] \propto \theta$ - occupied spaces on the grain
$[S] \propto 1-\theta$ - empty spaces on the grain, and
$[P] \propto c$ - vapor concentration of water in the intergranular space
Then, it can be rewritten as
$\alpha=\displaystyle\frac{\theta}{(1-\theta)c}$
with la constante de Langmuir ($\alpha$).
If we solve for la fracción de cobertura de agua ($\theta$), we obtain the degree of coverage as a function of water vapor pressure:
La fracción de cobertura de agua ($\theta$) se puede calcular con la constante de Langmuir ($\alpha$) y la concentración molar ($c_m$) con
Si se reeemplaza la concentración molar ($c_m$) con la presión de vapor de agua no saturado ($p_v$) empleando con la constante universal de los gases ($R_C$) y la temperatura absoluta ($T$) la ecuaci n
se observa que la constante de Langmuir ($\alpha$) puede ser reemplazado por un la constante de Langmuir ($\alpha_p$) resultando
El diferencial de la energía libre de Gibbs ($dG$) with la tensión superficial ($\sigma$), la variación de la superficie ($dS$), el volumen ($V$), and la variación de la presión ($dp$) leads to:
Integrating el diferencial de la energía libre de Gibbs ($dG$) from the state where there are no water molecules in the meniscus to the state where they reach saturated pressure requires two trivial integrals that yield la diferencia de la energía libre de Gibbs ($\Delta G$):
$\displaystyle\int dG = \Delta G$
and the integration of the entire la conductividad térmica ($\lambda$):
$\displaystyle\int \sigma dS = \sigma S$
To integrate $Vdp$, it is important to remember that el volumen ($V$) results from the difference between the volume of the liquid $V_l$ and the gas $V_g$:
$\Delta V = V_l - V_g \sim - V$
since $V_l\ll V_g$.
Furthermore, if we consider the ideal gas equation with la constante universal de los gases ($R_C$)
the third integral becomes
$-nRT\displaystyle\int_{p_v}^{p_s}\displaystyle\frac{dp}{p}=-nRT\ln\left(\displaystyle\frac{p_s}{p_v}\right)$
With these considerations, la diferencia de la energía libre de Gibbs ($\Delta G$) can be expressed as:
La suma de la diferencia de la energía libre de Gibbs ($\Delta G$) junto con la tensión superficial ($\sigma$), la sección ($S$), la presión de vapor de agua no saturado ($p_v$), la presión de vapor de agua saturado ($p_s$), el volumen ($V$), el volumen molar ($V_m$), la temperatura absoluta ($T$) y la constante universal de los gases ($R_C$) se iguala a:
La integral de la sección ($S$) para dos granos de el radio de un grano genérico ($r_0$) con un menisco de agua de el radio del menisco ($r_m$) en el l mite $r_m\ll r_0$ es igual a:
$S=4\pi \displaystyle\int_0^{r_0r_m/(r_0+r_m)}du[\sqrt{r_0^2+2r_mr_0}-\sqrt{r_m^2-u^2}]\sim 4\pi \sqrt{2r_0r_m^3}$
Y para el volumen ($V$),
$V=4\pi\displaystyle\int_0^{r_0r_m/(r_0+r_m)}du[r_m^2+r_0(r_m-u)-\sqrt{(r_m(r_m+2r_0)(r_m^2-u^2)}]\sim 2\pi r_0 r_m^2$
As que, con la definici n de la humedad relativa ($RH$),
obtenemos:
Para minimizar la diferencia de la energía libre de Gibbs ($\Delta G$) con la tensión superficial ($\sigma$), el radio del menisco ($r_m$), el radio de un grano genérico ($r_0$), la constante universal de los gases ($R_C$), la temperatura absoluta ($T$) y la humedad relativa ($RH$), definimos el radio del menisco ($r_m$) de la siguiente manera:
Podemos derivar la diferencia de la energía libre de Gibbs ($\Delta G$) con respecto a el radio del menisco ($r_m$) y establecer la derivada en cero para encontrar el valor de el radio del menisco ($r_m$) que minimiza la diferencia de la energía libre de Gibbs ($\Delta G$). Esto nos lleva a la siguiente ecuaci n:
$\displaystyle\frac{\partial\Delta G}{\partial r_m} = 6 \pi \sqrt{2 r_0 r_m } \sigma - 4 \pi r_m r_0 \displaystyle\frac{ R T }{ V_m }\ln\left(\displaystyle\frac{1}{ RH }\right)$
Resolviendo para el radio del menisco ($r_m$), obtenemos:
Ejemplos
Las mol culas de agua que se encuentran en forma de vapor pueden ser capturadas por la superficie de los granos. Esta absorci n se produce debido a las fuerzas intermoleculares.
Por otro lado, debido a las oscilaciones t rmicas, una mol cula absorbida puede adquirir suficiente energ a para liberarse.
Se alcanza un estado de equilibrio cuando la cantidad de part culas absorbidas es igual a la cantidad que logra liberarse nuevamente.
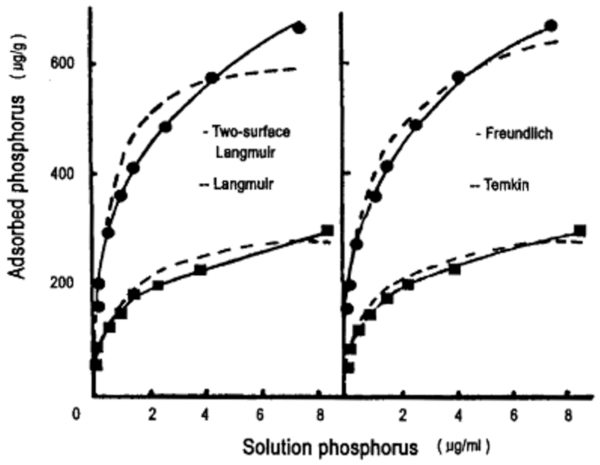
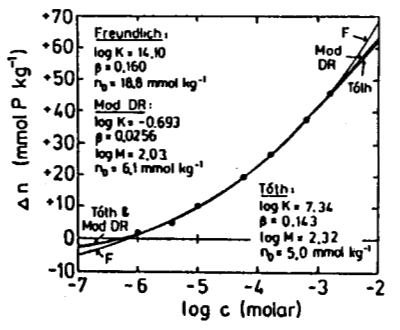
Cuando se compara el modelo de Langmuir con sistemas reales, se observan discrepancias significativas. Por esta raz n, han surgido varios modelos que se basan en el ajuste de curvas a datos experimentales.
En la gr fica mostrada, se presentan los modelos de Langmuir de una y dos capas en el lado izquierdo, junto con los modelos de Freundlich y Temkin:
[1] "A comparison of the Langmuir, Freundlich and Temkin equations to describe phosphate adsorption properties of soil." (Una comparaci n de las ecuaciones de Langmuir, Freundlich y Temkin para describir las propiedades de adsorci n de fosfato del suelo), Mead, J.A., Aust. J. Soil Res. 19:333-342 (1981)
Las mol culas en el interior de un l quido experimentan atracciones equitativas hacia todas sus vecinas. Esto resulta en que, en suma, las fuerzas ejercidas se anulan mutuamente, lo que hace que la mol cula se comporte como una part cula libre.
Sin embargo, la situaci n es diferente para las mol culas en la superficie. Dado que hay m s mol culas en el interior del l quido que generan una fuerza efectiva hacia adentro, esto evita que las mol culas en la superficie abandonen el l quido.
La fuerza descrita en la l mina anterior da origen a lo que se conoce como ERROR:tensi n superficial. Esta tensi n superficial crea una especie de membrana en la superficie, lo que permite que algunos insectos se desplacen sobre ella sin hundirse. Por ejemplo, la pata de la ara a en la imagen no perfora la superficie, evitando as que se hunda.
La tensi n superficial tambi n es responsable de la forma de las gotas de agua. La atracci n entre las mol culas tiende a hacer que la gota tenga la menor superficie posible, lo que significa que buscar asumir una forma esf rica. Esto provoca que un chorro de agua tienda a romperse en gotas, y estas gotas tienden a ser esf ricas o fluctuar en torno a esta forma.
La capilaridad provoca que el agua se acumule entre los granos del suelo. Se forma un menisco alrededor de la zona de uni n, como se muestra en la imagen con las flechas rojas:
la tensión superficial ($\sigma$) genera una presi n interna la presión por tensión superficial ($p_c$), que depende de ERROR:4962,0, contrarrestando la presi n sobre el menisco generado la presión de vapor de agua no saturado ($p_v$).
El efecto final del menisco es generar una fuerza que une los granos del suelo, proporcionando cohesi n, lo cual es fundamental para las propiedades mec nicas del suelo.
Por otro lado, la misma tensi n dificulta la eliminaci n del agua del suelo durante los procesos de secado.
Para ilustrar, consideremos la construcci n de castillos de arena en la playa. Si agregamos demasiada agua a la arena, los meniscos no se forman (el radio es mayor que el grano), y la arena no es moldeable. Por otro lado, a medida que el sol seca la arena, se pierde la cohesi n y el castillo se derrumba.
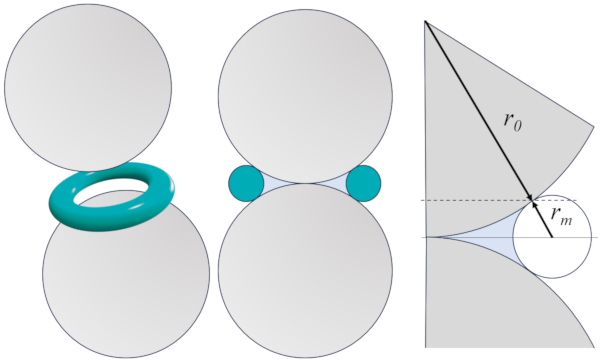
La geometr a est definida por dos granos que se asumen como esferas de el radio de un grano genérico ($r_0$) en contacto en un punto. En esta zona, se forma una regi n con agua que, gracias a la tensión superficial ($\sigma$), se concentra alrededor del punto de contacto y crea un menisco de el radio del menisco ($r_m$) en su entorno, de manera similar a si existiera un toro imaginario, como se muestra en la imagen a continuaci n:
&bull: la sección ($S$) corresponde a la l nea del toro imaginario entre los dos puntos de contacto entre el grano y el toro, que luego debe ser rotada en torno a un eje que pasa por los dos centros de los granos.
&bull: el volumen ($V$) corresponde al rea celeste que luego debe ser rotada en torno a un eje que pasa por los dos centros de los granos.
Las mol culas de agua pueden ser adsorbidas por la superficie de los granos, es decir, capturadas y retenidas mediante fuerzas intermoleculares.
La cantidad retenida depende tanto de estas fuerzas intermoleculares como de la concentraci n o presi n del vapor de agua presente en la superficie.
En 1918, Langmuir [1] estudi el equilibrio entre un gas de part culas asociado a la concentración segunda componente ($[P]$), los espacios vac os asociados a la concentración primera componente ($[S]$) y los espacios ocupados asociados a la concentración componente reaccionada ($[SP]$):
$S + P\rightleftharpoons SP$
Propuso que las concentraciones cumplen una ecuaci n del tipo:
[1] "The Adsorption of Gases on Plane Surfaces of Glass, Mica, and Platinum" (La adsorci n de gases en superficies planas de vidrio, mica y platino), Irving Langmuir, Journal of the American Chemical Society, Volume 40, Issue 9, pages 1361-1403 (1918).
Bas ndonos en la suposici n de que las concentraciones en una reacci n qu mica pueden compararse con las 'componentes': las mol culas de agua en el aire (la concentración segunda componente ($[P]$)), los espacios vac os sobre el grano (la concentración primera componente ($[S]$)), y los lugares ocupados (la concentración componente reaccionada ($[SP]$)), podemos modelar la cobertura del grano con la relaci n en el cociente de concentración ($K$):
De esta manera, utilizando la concentración molar ($c_m$), la fracción de cobertura de agua ($\theta$) y la constante de Langmuir ($\alpha$) [1], obtenemos el grado de cobertura en funci n de la presi n de vapor de agua:
El significado f sico de la constante de Langmuir es un coeficiente de afinidad de la superficie del grano con el agua. Cuanto mayor sea su valor, mayor ser la probabilidad de que las mol culas de agua se adhieran a la superficie.
[1] "The Constitution and Fundamental Properties of Solids and Liquids. Part I. Solids" (La Constituci n y Propiedades Fundamentales de S lidos y L quidos. Parte I. S lidos) - Irving Langmuir, Journal of the American Chemical Society, Volume 38, Issue 11, p ginas 2221-2295 (1916).
La obtenci n de la fracción de cobertura de agua ($\theta$) se basa en la concentración de particulas ($c_n$) y, por lo tanto, puede expresarse en funci n de la presión de vapor de agua no saturado ($p_v$) utilizando la constante universal de los gases ($R_C$) y la temperatura absoluta ($T$) mediante la ecuaci n:
En este caso, la constante de Langmuir ($\alpha$) puede ser sustituido por la constante de Langmuir ($\alpha_p$) utilizando la ecuaci n:
Se puede consultar un art culo que describe c mo estimar la constante de Langmuir en [1]. Otro art culo estudia la absorci n de diferentes iones en la superficie de los granos [2]. Para una constante de Langmuir ($\alpha$) del orden de 1000 L/mol, como se describe en el art culo, la constante de Langmuir ($\alpha_p$) ser de aproximadamente 4.1E-4 1/Pa a temperatura ambiente.
[1] "Evaluation of thermodynamic parameters of cadmium adsorption on sand from Temkin adsorption isotherm" (Evaluaci n de los par metros termodin micos de la adsorci n de cadmio en arena de la isoterma de adsorci n de Temkin), Abdul Satter Ali Khan, Turk J. Chem 36, 437-443 (2012).
[2] "A Comparison of the Langmuir, Freundlich and Temkin Equations to Describe Phosphate Sorption Characteristics of Some Representative Soils of Bangladesh" (Una comparaci n de las ecuaciones de Langmuir, Freundlich y Temkin para describir las caracter sticas de sorci n de fosfato de algunos suelos representativos de Bangladesh), Mohammad Z. Afsar, Sirajul Hoque, K.T. Osman, International Journal of Soil Science 7 (3): 91-99 (2012).
La fracción de cobertura de agua ($\theta$) se calcula en funci n de la concentración de particulas ($c_n$), lo que permite su reescritura en t rminos de la presión de vapor de agua no saturado ($p_v$) utilizando la constante universal de los gases ($R_C$) y la temperatura absoluta ($T$) a trav s de la ecuaci n:
En este caso, la expresi n para la fracción de cobertura de agua ($\theta$) se puede reescribir en t rminos de la presión de vapor de agua no saturado ($p_v$) como sigue:
La presión ($p$), el volumen ($V$), la temperatura absoluta ($T$), y el número de moles ($n$) est n relacionados por la siguiente ecuaci n:
donde la constante universal de los gases ($R_C$) tiene el valor de 8.314 J/K mol.
El número de moles ($n$) se determina dividiendo el volumen ($V$) de una sustancia por su el volumen molar ($V_m$), que corresponde al peso de un mol de la sustancia.
Por lo tanto, se puede establecer la siguiente relaci n:
El volumen molar se expresa en metros c bicos por mol ($m^3/mol$).
Es importante tener en cuenta que el volumen molar depende de las condiciones de presi n y temperatura en las que se encuentra la sustancia, especialmente en el caso de un gas, por lo que se define considerando las condiciones espec ficas.
En general, el diferencial de la energía libre de Gibbs ($dG$) es igual a la entropía ($S$), la variación de la temperatura ($dT$), el volumen ($V$), y la variación de la presión ($dp$), lo cual se expresa de la siguiente manera:
Durante un cambio de fase, es necesario tener en cuenta la diferencia de esta expresi n entre las dos fases. Sin embargo, en este caso, la temperatura absoluta ($T$) no var a, por lo que el t rmino $SdT$ no aparece. Por otro lado, al considerar la variaci n de los t rminos el volumen ($V$) y la variación de la presión ($dp$), se abarca la variación de volumen en cambio de fase ($\Delta V$). Finalmente, es necesario incluir el t rmino la tensión superficial ($\sigma$) y la variación de la superficie ($dS$):
En general, el diferencial de la energía libre de Gibbs ($dG$) es igual a la tensión superficial ($\sigma$), la variación de la superficie ($dS$), el volumen ($V$) y la variación de la presión ($dp$), lo cual se expresa de la siguiente manera:
Sin embargo, en el caso del menisco de agua, la temperatura absoluta ($T$) no var a, pero la superficie s cambia a medida que m s mol culas se condensan dentro de el volumen ($V$) de agua. Por lo tanto, al integrar desde la ausencia de mol culas de agua hasta alcanzar el estado de equilibrio, se obtiene la diferencia de la energía libre de Gibbs ($\Delta G$) en t rminos de la sección ($S$), la presión de vapor de agua no saturado ($p_v$), la presión de vapor de agua saturado ($p_s$), el volumen molar ($V_m$), y la constante universal de los gases ($R_C$):
La humedad relativa ($RH$) se puede expresar en t rminos de la presión de vapor de agua no saturado ($p_v$) y la presión de vapor de agua saturado ($p_s$) de la siguiente manera:
La diferencia de la energía libre de Gibbs ($\Delta G$) con la tensión superficial ($\sigma$), la sección ($S$), la presión de vapor de agua no saturado ($p_v$), la presión de vapor de agua saturado ($p_s$), el volumen ($V$), el volumen molar ($V_m$), la temperatura absoluta ($T$) y la constante universal de los gases ($R_C$) se iguala a:
Para calcular la diferencia de la energía libre de Gibbs ($\Delta G$), debemos calcular la tensión superficial ($\sigma$) y el volumen ($V$) para el mensico de radio el radio del menisco ($r_m$) que se forma entre los granos, suponiendo un valor de el radio de un grano genérico ($r_0$):
La suma de la diferencia de la energía libre de Gibbs ($\Delta G$) con la tensión superficial ($\sigma$), el radio del menisco ($r_m$), el radio de un grano genérico ($r_0$), la constante universal de los gases ($R_C$), la temperatura absoluta ($T$) y la humedad relativa ($RH$) es igual a:
El valor de el radio del menisco ($r_m$) debe ser elegido de manera que la diferencia de la energía libre de Gibbs ($\Delta G$) sea m nimo. Para lograr esto, podemos derivar la diferencia de la energía libre de Gibbs ($\Delta G$) con respecto a el radio del menisco ($r_m$), igualar la derivada a cero y resolver para el radio del menisco ($r_m$). Esto nos da:
ID:(374, 0)