mechanisms

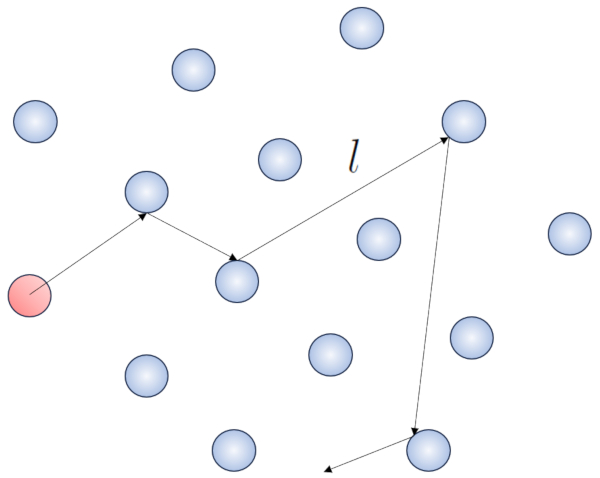
Cuando una part cula de un gas se desplaza, interact a con las dem s part culas en su entorno. La forma m s simple de esta interacci n es a trav s de choques el sticos, lo que significa que la part cula choca sin perder energ a, cambiando su direcci n para luego impactar con otra part cula.

image

Dentro de este proceso, tiene sentido definir el camino libre ($\bar{l}$), cuyo valor depender de una concentración de particulas ($c_n$).

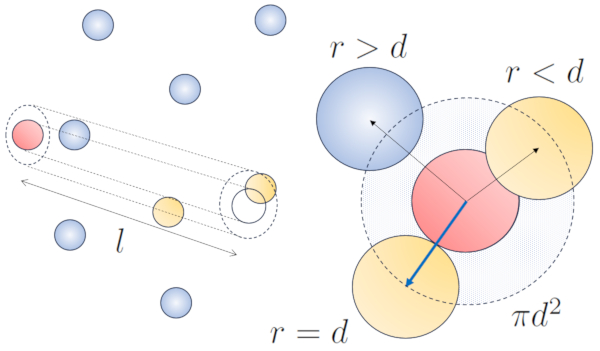
Cuando una part cula de un radio dado se desplaza en el espacio, efectivamente ocupa el espacio de un cilindro con el mismo radio. Para que esta part cula colisione con otra, esta segunda debe tener parte de su volumen dentro de dicho cilindro. En el caso m s extremo, la segunda part cula se encuentra a una distancia de dos radios del primero, de manera que el borde del cilindro est en contacto con un punto de la esfera m s cercano al eje del cilindro. El centro de esta esfera se encuentra a una distancia igual a un radio desde la superficie del cilindro:

image

Por lo tanto, la distancia entre el eje del cilindro y el centro de cualquier part cula es de dos radios, es decir, un di metro. En otras palabras, se puede concebir que el volumen ocupado de manera literal por la part cula que se desplaza en el espacio es un cilindro con una longitud igual al camino libre y un radio igual al di metro de la propia part cula.

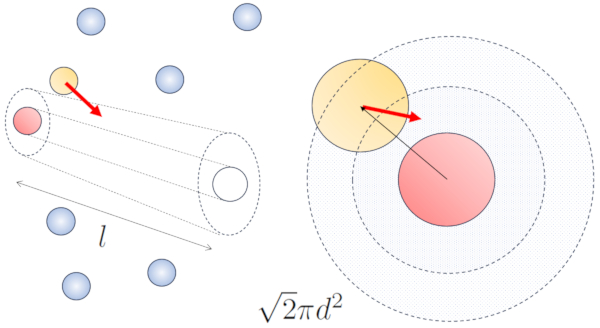
Cuando las part culas vecinas est n en movimiento, existe una mayor probabilidad de colisi n debido a que durante el mismo intervalo de tiempo, recorren una mayor distancia. Las componentes de velocidad, $v_x$, $v_y$, y $v_z$, fluct an alrededor de valores medios $\sqrt{\langle v_x^2\rangle}$, $\sqrt{\langle v_y^2\rangle}$ y $\sqrt{\langle v_z^2\rangle}$. Si asumimos que el sistema es isotr pico, el promedio de cada componente ser igual a $\displaystyle\frac{1}{3}\sqrt{\langle v^2\rangle}$. Por lo tanto, en el eje a lo largo del cual se desplaza la part cula, recorrer una distancia

$\sqrt{\langle v_z^2\rangle}dt=\displaystyle\frac{1}{3}\sqrt{\langle v^2\rangle}dt$

Al mismo tiempo, las part culas que se desplazan perpendicularmente habr n recorrido una distancia:

$\sqrt{\langle v_x^2\rangle+\langle v_y^2\rangle}dt=\displaystyle\frac{\sqrt{2}}{3}\sqrt{\langle v^2\rangle}dt$

Por lo tanto, la probabilidad de colisi n aumentar en un factor de $\sqrt{2}$ en comparaci n con el caso en el que las part culas no se desplazan:

image

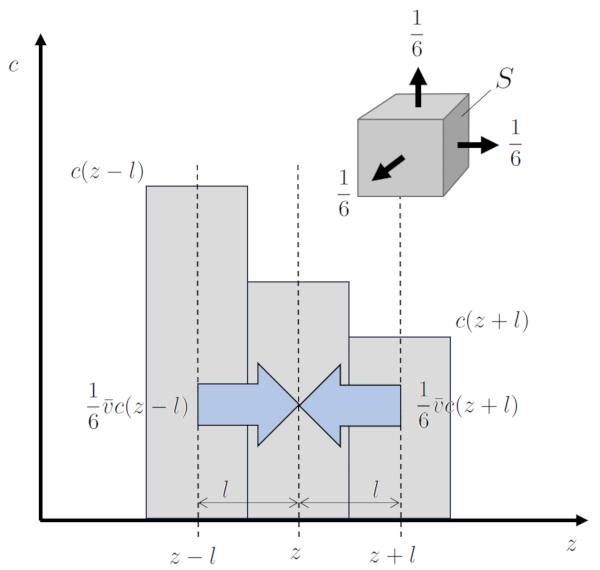
Si hay una diferencia espacial en la concentración de particulas ($c_n$), se genera un fen meno conocido como ERROR:6597,0. La probabilidad de que las part culas lleguen a una posición a lo largo de un eje ($z$) desde una posici n anterior a una distancia de el camino libre ($\bar{l}$) es diferente de la probabilidad desde una posici n posterior a la misma distancia. Esto conduce a cambios en la concentración de particulas ($c_n$), lo que se denomina difusi n. La velocidad a la que ocurre este proceso es la de la velocidad media de una partícula ($\bar{v}$), y en l participa siempre $1/6$ de las part culas en cada direcci n, ya que hay $6$ direcciones en un espacio tridimensional.

image

De esta manera, se genera la densidad de flujo de partículas ($j$), que en t rminos de rea corresponde a:

$j=\displaystyle\frac{1}{6}\bar{v}c(z-\bar{l}) - \displaystyle\frac{1}{6}\bar{v}c(z+\bar{l})=\displaystyle\frac{1}{6}\bar{v}[c(z-\bar{l})-c(z+\bar{l})]=-\displaystyle\frac{1}{6}\bar{v}2\bar{l}\displaystyle\frac{dc}{dz}$

Las constantes que se factorizan al calcular la densidad de flujo de partículas ($j$) se resumen en una constante que se denomina la constante de difusión ($D$) y que es igual a un tercio del producto de el camino libre ($\bar{l}$) y la velocidad media de una partícula ($\bar{v}$).

El c lculo de la densidad de flujo de partículas ($j$) en funci n de la variación de concentración ($dc_n$), ERROR:10192,0 y la constante de difusión ($D$):

equation=4820

nos permite determinar c mo se evapora el agua de la capa fre tica. Para ello, se deben seguir los siguientes pasos:

• Obtener la temperatura ambiente, la humedad relativa, la porosidad del suelo y la profundidad de la capa fre tica.

• Calcular la temperatura del agua en la superficie de la capa fre tica.

• Calcular la concentraci n saturada de vapor de agua sobre la capa fre tica.

• Calcular la concentraci n de vapor de agua sobre el suelo.

• Calcular el flujo de vapor de agua para el l mite de flujo estacionario.

model

La concentración molar ($c_m$) corresponde al ERROR:9339,0 por el volumen ($V$) de un gas y se calcula como sigue:

kyon

El número de moles ($n$) corresponde a el número de partículas ($N$) dividido por el número de Avogadro ($N_A$):

kyon

el número de Avogadro ($N_A$) es una constante universal cuyo valor es 6.028E+23 1/mol, por lo que no se incluye entre las variables asociadas al c lculo.

Para convertir la concentración molar ($c_m$) en la concentración de particulas ($c_n$), simplemente multiplique la primera por el número de Avogadro ($N_A$), as :

kyon

El número de moles ($n$) se determina dividiendo la masa ($M$) de una sustancia por su la masa molar ($M_m$), que corresponde al peso de un mol de la sustancia.

Por lo tanto, se puede establecer la siguiente relaci n:

kyon

La masa molar se expresa en gramos por mol (g/mol).

Si dividimos la densidad ($\rho$) por la masa de la partícula ($m$), obtendremos la concentración de particulas ($c_n$):

kyon

El camino libre medio se puede estimar en funci n del di metro de un cilindro imaginario que rodea una part cula, teniendo en promedio una colisi n con otra part cula.

El radio del cilindro corresponde a la distancia m xima que dos part culas deben tener para colisionar, lo que equivale a dos veces el radio de la part cula, es decir, el diámetro de la partícula ($d$). Dado que solo ocurre una colisi n en este cilindro, el n mero de part culas contenidas en l debe ser igual a uno. Esto significa que:

$l d^2\pi c_n= 1$

con la concentración de particulas ($c_n$) y resolviendo para el camino libre ($\bar{l}$), obtenemos:

kyon

Esto representa el camino libre medio.

Para el caso sin movimiento, la probabilidad es de el camino libre ($\bar{l}$), mientras que con movimiento, las probabilidades son de el diámetro de la partícula ($d$) y la concentración de particulas ($c_n$), respectivamente.

equation=3942

En el caso del movimiento, la probabilidad se incrementa en un factor de $\sqrt{2}$, lo que significa que el camino libre es

kyon

La energía cinética ($K$) junto con la masa de la partícula ($m$) y la velocidad media de una partícula ($\bar{v}$) es igual a

kyon

Nota: En un rigor m s estricto, la energ a cin tica depende del promedio de la velocidad al cuadrado $\bar{v^2}$. Sin embargo, se asume que este es aproximadamente igual al cuadrado del promedio de la velocidad:

$\bar{v^2}\sim\bar{v}^2$

La masa de la partícula ($m$) puede estimarse a partir de la masa molar ($M_m$) y el número de Avogadro ($N_A$) mediante

kyon

La ley de Stefan-Boltzmann, inicialmente propuesta por Josef Stefan [1] y posteriormente refinada por Ludwig Boltzmann [2], establece que la energía de una molécula ($E$) es proporcional a el grados de libertad ($f$) multiplicado por la temperatura absoluta ($T$) con una constante de proporcionalidad la constante de Boltzmann ($k_B$):

kyon

Es importante destacar que la temperatura absoluta ($T$) debe expresarse necesariamente en grados Kelvin.

El n mero de grados de libertad de una part cula corresponde al n mero de variables necesarias para describir su estado termodin mico. Por ejemplo, para una part cula puntual, se requieren solo tres coordenadas, lo que da lugar a tres grados de libertad. Si la part cula tiene forma y es r gida, se necesitan adem s dos ngulos, lo que resulta en un total de cinco grados de libertad. Cuando la part cula puede deformarse o vibrar en una o m s direcciones, estos modos adicionales tambi n se consideran grados de libertad. Sin embargo, es importante notar que estos grados de libertad adicionales solo existen a altas temperaturas, cuando la part cula tiene suficiente energ a para activar dichas vibraciones.

[1] " ber die Beziehung zwischen der W rmestrahlung und der Temperatur" (Sobre la relaci n entre la radiaci n de calor y la temperatura), Josef Stefan, Sitzungsberichte der mathematisch-naturwissenschaftlichen Classe der Kaiserlichen Akademie der Wissenschaften, Wien (1879).

[2] "Weitere Studien ber das W rmegleichgewicht unter Gasmolek len" (M s estudios sobre el equilibrio t rmico entre mol culas de gas), Ludwig Boltzmann, Sitzungsberichte der mathematisch-naturwissenschaftlichen Classe der Kaiserlichen Akademie der Wissenschaften, Wien (1884).

Si se iguala la energía cinética ($K$) con la energía de una molécula ($E$) se puede calcular en funci n de el grados de libertad ($f$), la constante de Boltzmann ($k_B$), la temperatura absoluta ($T$) y la masa de la partícula ($m$) lo que es la velocidad media de una partícula ($\bar{v}$) mediante

kyon

La constante de difusión ($D$) se puede calcular a partir de la velocidad media de una partícula ($\bar{v}$) y de el camino libre ($\bar{l}$) de las part culas.

kyon

Es importante reconocer que tanto el camino libre como la velocidad media dependen de la temperatura, y por lo tanto, tambi n lo hace la constante de difusi n. Por esta raz n, cuando se publican valores para la llamada constante, siempre se indica la temperatura a la que se refiere.

En 1855, Adolf Fick [1] formul una ecuaci n para el c lculo de la constante de difusión ($D$), que resulta en la densidad de flujo de partículas ($j$) debido a la variación de concentración ($dc_n$) a lo largo de ERROR:10192,0:

kyon

[1] " ber Diffusion" (Sobre difusi n), Adolf Fick, Annalen der Physik und Chemie, Volume 170, p ginas 59-86 (1855)

El c lculo de la densidad de flujo de partículas ($j$) en una dimensi n se realiza utilizando los valores la constante de difusión ($D$), la concentración de particulas ($c_n$) y la posición a lo largo de un eje ($z$), de acuerdo con la siguiente ley de Fick [1]:

equation=4820

Esta f rmula se puede generalizar para m s de una dimensi n seg n:

kyon

[1] " ber Diffusion" (Sobre difusi n), Adolf Fick, Annalen der Physik und Chemie, Volume 170, p ginas 59-86 (1855)

Si la constante de difusión ($D$) es igual a la densidad de flujo de partículas ($j$) debido a la variación de concentración ($dc_n$) a lo largo de ERROR:10192,0, esto se rige por la ley de Fick [1]:

equation=4820

Por lo tanto, para describir la variaci n de la concentraci n en el tiempo ($t$), que corresponde a la variaci n espacial de la densidad de flujo, obtenemos la ecuaci n

kyon

[1] " ber Diffusion" (Sobre difusi n), Adolf Fick, Annalen der Physik und Chemie, Volumen 170, p ginas 59-86 (1855)