Absorption d'eau dans les grains
Storyboard 
La vapeur d'eau interagit avec la surface des grains du sol, formant ainsi des couches d'eau à leur surface. Le degré de couverture dépend de la pression de la vapeur d'eau existante.
ID:(374, 0)
Absorption d'eau dans les grains
Storyboard 
La vapeur d'eau interagit avec la surface des grains du sol, formant ainsi des couches d'eau à leur surface. Le degré de couverture dépend de la pression de la vapeur d'eau existante.
Variables
Calculs
Calculs
Équations
A pression ($p$), le volume ($V$), a température absolue ($T$) et le nombre de taupes ($n$) sont li s par les lois physiques suivantes :
• Loi de Boyle
• Loi de Charles
• Loi de Gay-Lussac
• Loi d'Avogadro
Ces lois peuvent tre exprim es de mani re plus g n rale comme suit :
$\displaystyle\frac{pV}{nT}=cte$
Cette relation g n rale tablit que le produit de la pression et du volume divis par le nombre de moles et la temp rature reste constant :
A fraction de couverture d'eau ($\theta$) peut tre calcul en utilisant a constante de Langmuir ($\alpha$) et a concentration molaire ($c_m$) avec l' quation :
Si nous rempla ons a concentration molaire ($c_m$) par a pression de vapeur d'eau non saturée ($p_v$) en utilisant a constante du gaz universel ($R_C$) et a température absolue ($T$) travers l' quation :
il devient vident que a constante de Langmuir ($\alpha$) peut tre remplac par a constante de Langmuir ($\alpha_p$) en utilisant l' quation :
ce qui donne :
La relation entre a humidité relative ($RH$) avec a concentration de molécules de vapeur d'eau ($c_v$) et ERROR:4952,0 est exprim e comme suit :
et en reliant a pression ($p$) avec a concentration molaire ($c_m$), a température absolue ($T$), et a constante du gaz universel ($R_C$), nous obtenons :
Cela s'applique la pression de vapeur d'eau, o :
$p_v = c_v R T$
et la pression de vapeur satur e de l'eau :
$p_s = c_s R T$
ce qui donne l' quation suivante :
$ \theta =\displaystyle\frac{ \alpha c_m }{1+ \alpha c_m }$
theta = alpha * c_m /(1+ alpha * c_m )
En consid rant les espaces occup s a concentration du deuxième composant ($[P]$), les espaces vides associ s a concentration du premier composant ($[S]$), et les espaces occup s associ s a concentration des composants ayant réagi ($[SP]$) et le quotient de concentration ($K$) :
Si a fraction de couverture d'eau ($\theta$) repr sente la fraction de surface occup e par les mol cules :
$[SP] \propto \theta$ - espaces occup s sur le grain
$[S] \propto 1-\theta$ - espaces vides sur le grain, et
$[P] \propto c$ - concentration de vapeur d'eau dans l'espace intergranulaire
Alors, cela peut tre exprim comme
$\alpha=\displaystyle\frac{\theta}{(1-\theta)c}$
avec a constante de Langmuir ($\alpha$).
En r solvant pour a fraction de couverture d'eau ($\theta$), nous pouvons obtenir le degr de couverture en fonction de la pression de vapeur d'eau :
Le différentiel d'énergie libre de Gibbs ($dG$) avec a tension superficielle ($\sigma$), a variation de surface ($dS$), le volume ($V$) et a variation de pression ($dp$) peut s'exprimer comme suit :
L'int gration de le différentiel d'énergie libre de Gibbs ($dG$) depuis l' tat o il n'y a pas de mol cules d'eau dans le m nisque jusqu' l' tat d' quilibre requiert deux int grales triviales qui donnent a différence d'énergie libre de Gibbs ($\Delta G$) :
$\displaystyle\int dG = \Delta G$
et l'int gration de l'ensemble de a conductivité thermique ($\lambda$) :
$\displaystyle\int \sigma dS = \sigma S$
Pour int grer $Vdp$, il est important de noter que le volume ($V$) r sulte de la diff rence entre le volume du liquide $V_l$ et celui du gaz $V_g$ :
$\Delta V = V_l - V_g \sim - V$
car $V_l\ll V_g$.
De plus, si nous prenons en compte l' quation des gaz parfaits avec a constante du gaz universel ($R_C$)
la troisi me int grale devient
$-nRT\displaystyle\int_{p_v}^{p_s}\displaystyle\frac{dp}{p}=-nRT\ln\left(\displaystyle\frac{p_s}{p_v}\right)$
En tenant compte de ces consid rations, a différence d'énergie libre de Gibbs ($\Delta G$) peut tre exprim comme suit :
La somme de a différence d'énergie libre de Gibbs ($\Delta G$) avec a tension superficielle ($\sigma$), a section ($S$), a pression de vapeur d'eau non saturée ($p_v$), a pression de vapeur d'eau saturée ($p_s$), le volume ($V$), le volume molaire ($V_m$), a température absolue ($T$), et a constante du gaz universel ($R_C$) est gale :
L'int grale de a section ($S$) pour deux grains de le rayon d'un grain générique ($r_0$) avec un m nisque d'eau de le rayon du ménisque ($r_m$) dans la limite $r_m\ll r_0$ est donn e par :
$S=4\pi \displaystyle\int_0^{r_0r_m/(r_0+r_m)}du[\sqrt{r_0^2+2r_mr_0}-\sqrt{r_m^2-u^2}]\sim 4\pi \sqrt{2r_0r_m^3}$
Et pour le volume ($V$),
$V=4\pi\displaystyle\int_0^{r_0r_m/(r_0+r_m)}du[r_m^2+r_0(r_m-u)-\sqrt{(r_m(r_m+2r_0)(r_m^2-u^2)}]\sim 2\pi r_0 r_m^2$
Ainsi, avec la d finition de a humidité relative ($RH$),
nous obtenons :
Pour que a différence d'énergie libre de Gibbs ($\Delta G$) soit minimis avec a tension superficielle ($\sigma$), le rayon du ménisque ($r_m$), le rayon d'un grain générique ($r_0$), a constante du gaz universel ($R_C$), a température absolue ($T$) et a humidité relative ($RH$), nous d finissons le rayon du ménisque ($r_m$) comme suit :
Nous pouvons d river a différence d'énergie libre de Gibbs ($\Delta G$) par rapport le rayon du ménisque ($r_m$) et galiser la d riv e z ro pour trouver la valeur de le rayon du ménisque ($r_m$) qui minimise a différence d'énergie libre de Gibbs ($\Delta G$). Cela nous conduit l' quation suivante :
$\displaystyle\frac{\partial\Delta G}{\partial r_m} = 6 \pi \sqrt{2 r_0 r_m } \sigma - 4 \pi r_m r_0 \displaystyle\frac{ R T }{ V_m }\ln\left(\displaystyle\frac{1}{ RH }\right)$
En r solvant pour le rayon du ménisque ($r_m$), nous obtenons :
Exemples
Les mol cules d'eau suspendues sous forme de vapeur peuvent tre captur es par la surface des grains. Cette absorption est due aux forces intermol culaires.
D'autre part, en raison des oscillations thermiques, une mol cule absorb e peut acqu rir suffisamment d' nergie pour se lib rer.
Un tat d' quilibre est atteint lorsque le nombre de particules absorb es est gal au nombre de celles qui peuvent tre lib r es nouveau.
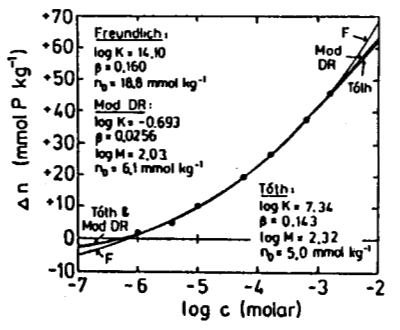
Lorsque l'on compare le mod le de Langmuir des syst mes r els, on observe des divergences significatives. C'est pourquoi plusieurs mod les ont t d velopp s, bas s sur l'ajustement de courbes des donn es exp rimentales.
Sur le graphique pr sent , on trouve les mod les de Langmuir une et deux couches du c t gauche, ainsi que les mod les de Freundlich et de Temkin :
[1] "A comparison of the Langmuir, Freundlich and Temkin equations to describe phosphate adsorption properties of soil." (Comparaison des quations de Langmuir, Freundlich et Temkin pour d crire les propri t s d'adsorption du phosphate dans le sol), Mead, J.A., Aust. J. Soil Res. 19:333-342 (1981).
Les mol cules l'int rieur d'un liquide subissent des attractions gales envers toutes leurs voisines. Cela a pour cons quence que les forces globalement exerc es s'annulent mutuellement, faisant en sorte que la mol cule se comporte comme une particule libre.
Cependant, la situation est diff rente pour les mol cules la surface. tant donn qu'il y a plus de mol cules l'int rieur du liquide g n rant une force effective vers l'int rieur, cela emp che les mol cules la surface de quitter le liquide.
La force d crite dans la section pr c dente donne naissance ce que l'on appelle la ERROR:tension superficielle. Cette tension superficielle cr e une sorte de membrane la surface, ce qui permet certains insectes de se d placer sur celle-ci sans couler. Par exemple, la patte de l'araign e sur l'image ne p n tre pas la surface, vitant ainsi de couler.
La tension superficielle est galement responsable de la forme des gouttes d'eau. L'attraction entre les mol cules tend faire en sorte que la goutte ait la plus petite surface possible, ce qui signifie qu'elle cherchera adopter une forme sph rique. Cela fait qu'un jet d'eau a tendance se briser en gouttes, et ces gouttes ont tendance tre sph riques ou fluctuer autour de cette forme.
La capillarit provoque l'accumulation de l'eau entre les grains du sol. Un m nisque se forme autour de la zone de jonction, comme indiqu par les fl ches rouges dans l'image ci-dessous :
a tension superficielle ($\sigma$) g n re une pression interne a pression de tension superficielle ($p_c$), qui d pend de ERROR:4962,0, contrecarrant la pression sur le m nisque g n r a pression de vapeur d'eau non saturée ($p_v$).
L'effet final du m nisque est de g n rer une force qui lie les grains du sol, fournissant une coh sion essentielle pour les propri t s m caniques du sol.
D'autre part, la m me tension entrave l' limination de l'eau du sol lors des processus de s chage.
Pour illustrer, envisagez la construction de ch teaux de sable sur la plage. Si nous ajoutons trop d'eau au sable, les m nisques ne se forment pas (le rayon est plus grand que le grain), et le sable n'est pas mall able. En revanche, lorsque le soleil s che le sable, la coh sion est perdue, et le ch teau s'effondre.
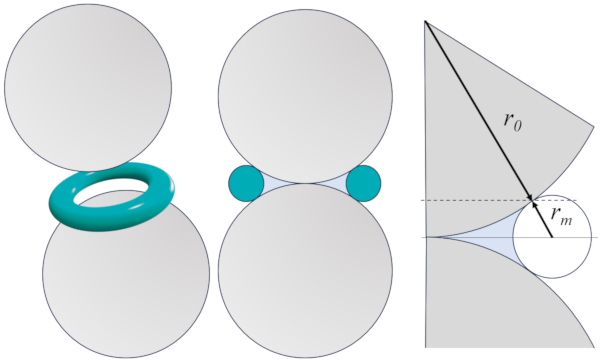
La g om trie est d finie par deux grains suppos s tre des sph res de le rayon d'un grain générique ($r_0$) en contact en un point. Dans cette r gion, une zone d'eau se forme, qui, gr ce a tension superficielle ($\sigma$), se concentre autour du point de contact et cr e un m nisque de le rayon du ménisque ($r_m$) dans son voisinage, de mani re similaire s'il existait un tore imaginaire, comme montr dans l'image ci-dessous :
&bull: a section ($S$) correspond la ligne du tore imaginaire entre les deux points de contact entre le grain et le tore, qui doit ensuite tre tourn e autour d'un axe passant par les deux centres des grains.
&bull: le volume ($V$) correspond la zone bleue, qui doit ensuite tre tourn e autour d'un axe passant par les deux centres des grains.
Les mol cules d'eau peuvent tre adsorb es par la surface des grains, c'est- -dire captur es et retenues par des forces intermol culaires.
La quantit retenue d pend la fois de ces forces intermol culaires et de la concentration ou de la pression de la vapeur d'eau pr sente la surface.
En 1918, Langmuir [1] a tudi l' quilibre entre un gaz de particules associ a concentration du deuxième composant ($[P]$), des espaces vides associ s a concentration du premier composant ($[S]$) et des espaces occup s associ s a concentration des composants ayant réagi ($[SP]$) :
$S + P\rightleftharpoons SP$
Il a propos que les concentrations ob issent une quation de ce type :
[1] "The Adsorption of Gases on Plane Surfaces of Glass, Mica, and Platinum" (L'adsorption des gaz sur des surfaces planes en verre, mica et platine) - Irving Langmuir, Journal of the American Chemical Society, Volume 40, Issue 9, pages 1361-1403 (1918).
En nous basant sur l'hypoth se que les concentrations dans une r action chimique peuvent tre compar es aux 'composants': les mol cules d'eau dans l'air (a concentration du deuxième composant ($[P]$)), les espaces vides la surface du grain (a concentration du premier composant ($[S]$)) et les emplacements occup s (a concentration des composants ayant réagi ($[SP]$)), nous pouvons mod liser la couverture du grain avec la relation en le quotient de concentration ($K$):
Ainsi, en utilisant a concentration molaire ($c_m$), a fraction de couverture d'eau ($\theta$) et a constante de Langmuir ($\alpha$) [1], nous obtenons le degr de couverture en fonction de la pression de vapeur d'eau :
La signification physique de la constante de Langmuir est un coefficient d'affinit de la surface du grain pour l'eau. Plus sa valeur est lev e, plus il est probable que les mol cules d'eau adh rent la surface.
[1] "The Constitution and Fundamental Properties of Solids and Liquids. Part I. Solids" (La Constitution et les Propri t s Fondamentales des Solides et des Liquides. Partie I. Solides) - Irving Langmuir, Journal of the American Chemical Society, Volume 38, Issue 11, pages 2221-2295 (1916).
L'obtention de a fraction de couverture d'eau ($\theta$) est bas e sur a concentration de particules ($c_n$) et peut donc tre exprim e en fonction de a pression de vapeur d'eau non saturée ($p_v$) en utilisant a constante du gaz universel ($R_C$) et a température absolue ($T$) via l' quation :
Dans ce cas, a constante de Langmuir ($\alpha$) peut tre remplac par a constante de Langmuir ($\alpha_p$) en utilisant l' quation :
Un article d crivant comment estimer la constante de Langmuir peut tre consult dans [1]. Un autre article tudie l'adsorption de diff rents ions la surface des grains [2]. Pour une constante de Langmuir ($\alpha$) de l'ordre de 1000 L/mol, tel que d crit dans l'article, a constante de Langmuir ($\alpha_p$) sera d'environ 4.1E-4 1/Pa temp rature ambiante.
[1] "Evaluation of thermodynamic parameters of cadmium adsorption on sand from Temkin adsorption isotherm" ( valuation des param tres thermodynamiques de l'adsorption du cadmium sur le sable partir de l'isotherme d'adsorption de Temkin), Abdul Satter Ali Khan, Turk J. Chem 36, 437-443 (2012).
[2] "A Comparison of the Langmuir, Freundlich and Temkin Equations to Describe Phosphate Sorption Characteristics of Some Representative Soils of Bangladesh" (Une comparaison des quations de Langmuir, Freundlich et Temkin pour d crire les caract ristiques d'adsorption du phosphate dans certains sols repr sentatifs du Bangladesh), Mohammad Z. Afsar, Sirajul Hoque, K.T. Osman, International Journal of Soil Science 7 (3) : 91-99 (2012).
A fraction de couverture d'eau ($\theta$) est calcul en fonction de a concentration de particules ($c_n$), ce qui permet de le r crire en termes de a pression de vapeur d'eau non saturée ($p_v$) en utilisant a constante du gaz universel ($R_C$) et a température absolue ($T$) travers l' quation :
Dans ce cas, l' quation pour a fraction de couverture d'eau ($\theta$) peut tre exprim e en termes de a pression de vapeur d'eau non saturée ($p_v$) comme suit :
A pression ($p$), le volume ($V$), a température absolue ($T$) et le nombre de taupes ($n$) sont li s par l' quation suivante :
o a constante du gaz universel ($R_C$) a une valeur de 8,314 J/K mol.
Le nombre de taupes ($n$) est d termin en divisant le volume ($V$) d'une substance par son le volume molaire ($V_m$), ce qui correspond au poids d'une mole de la substance.
Par cons quent, la relation suivante peut tre tablie :
Le volume molaire est exprim en m tres cubes par mole ($m^3/mol$).
Il est important de noter que le volume molaire d pend des conditions de pression et de temp rature dans lesquelles la substance se trouve, en particulier dans le cas d'un gaz. Il est donc d fini en tenant compte des conditions sp cifiques.
En g n ral, le différentiel d'énergie libre de Gibbs ($dG$) est gal a entropie ($S$), a variation de température ($dT$), le volume ($V$), et a variation de pression ($dp$), ce qui s'exprime comme suit :
Lors d'un changement de phase, il est n cessaire de prendre en compte la diff rence de cette expression entre les deux phases. Cependant, dans ce cas, a température absolue ($T$) ne varie pas, de sorte que le terme $SdT$ ne figure pas. D'autre part, en consid rant la variation des termes le volume ($V$) et a variation de pression ($dp$), cela comprend a variation de volume en changement de phase ($\Delta V$). Enfin, il faut inclure le terme a tension superficielle ($\sigma$) et a variation de surface ($dS$) :
En g n ral, le différentiel d'énergie libre de Gibbs ($dG$) est gal a tension superficielle ($\sigma$), a variation de surface ($dS$), le volume ($V$), et a variation de pression ($dp$), ce qui s'exprime comme suit :
Cependant, dans le cas du m nisque d'eau, a température absolue ($T$) ne varie pas, mais la surface change mesure que davantage de mol cules se condensent dans le volume ($V$) d'eau. Par cons quent, en int grant depuis l'absence de mol cules d'eau jusqu' atteindre l' tat d' quilibre, on obtient a différence d'énergie libre de Gibbs ($\Delta G$) en termes de a section ($S$), a pression de vapeur d'eau non saturée ($p_v$), a pression de vapeur d'eau saturée ($p_s$), le volume molaire ($V_m$), et a constante du gaz universel ($R_C$) :
A humidité relative ($RH$) peut tre exprim en termes de a pression de vapeur d'eau non saturée ($p_v$) et a pression de vapeur d'eau saturée ($p_s$) comme suitxa0:
A différence d'énergie libre de Gibbs ($\Delta G$) avec a tension superficielle ($\sigma$), a section ($S$), a pression de vapeur d'eau non saturée ($p_v$), a pression de vapeur d'eau saturée ($p_s$), le volume ($V$), le volume molaire ($V_m$), a température absolue ($T$) et a constante du gaz universel ($R_C$) quivaut :
Pour calculer a différence d'énergie libre de Gibbs ($\Delta G$), il est n cessaire de calculer a tension superficielle ($\sigma$) et le volume ($V$) pour le m nisque de rayon le rayon du ménisque ($r_m$), qui se forme entre les valeurs suppos es de le rayon d'un grain générique ($r_0$) :
La somme de a différence d'énergie libre de Gibbs ($\Delta G$) avec a tension superficielle ($\sigma$), le rayon du ménisque ($r_m$), le rayon d'un grain générique ($r_0$), a constante du gaz universel ($R_C$), a température absolue ($T$), et a humidité relative ($RH$) est gale :
Le choix de le rayon du ménisque ($r_m$) doit tre fait de mani re minimiser a différence d'énergie libre de Gibbs ($\Delta G$). Pour ce faire, nous pouvons d river a différence d'énergie libre de Gibbs ($\Delta G$) par rapport le rayon du ménisque ($r_m$), galer la d riv e z ro et r soudre pour le rayon du ménisque ($r_m$). Cela donne :
ID:(374, 0)