Absorção de Água em Grãos
Storyboard 
O vapor de água interage com a superfície dos grãos do solo, formando camadas de água em sua superfície. O grau de cobertura depende da pressão do vapor de água existente.
ID:(374, 0)
Absorção de Água em Grãos
Storyboard 
O vapor de água interage com a superfície dos grãos do solo, formando camadas de água em sua superfície. O grau de cobertura depende da pressão do vapor de água existente.
Variáveis
Cálculos
Cálculos
Equações
La pressão ($p$), o volume ($V$), la temperatura absoluta ($T$) e o número de moles ($n$) est o relacionados atrav s das seguintes leis f sicas:
• Lei de Boyle
• Lei de Charles
• Lei de Gay-Lussac
• Lei de Avogadro
Essas leis podem ser expressas de forma mais geral como:
$\displaystyle\frac{pV}{nT}=cte$
Essa rela o geral estabelece que o produto da press o e do volume dividido pelo n mero de moles e a temperatura permanece constante:
La fração de cobertura de água ($\theta$) pode ser calculado utilizando la constante de Langmuir ($\alpha$) e la concentração molar ($c_m$) com a equa o:
Se substituirmos la concentração molar ($c_m$) por la pressão de vapor de água insaturada ($p_v$) usando la constante de gás universal ($R_C$) e la temperatura absoluta ($T$) atrav s da equa o:
torna-se evidente que la constante de Langmuir ($\alpha$) pode ser substitu do por la constante de Langmuir ($\alpha_p$) usando a equa o:
resultando em:
A rela o entre la umidade relativa ($RH$) com la concentração de moléculas de vapor de água ($c_v$) e ERROR:4952,0 expressa como:
e relacionando la pressão ($p$) com la concentração molar ($c_m$), la temperatura absoluta ($T$) e la constante de gás universal ($R_C$), obtemos:
Isso se aplica press o de vapor de gua, onde:
$p_v = c_v R T$
e press o de vapor saturada de gua:
$p_s = c_s R T$
resultando na seguinte equa o:
$ \theta =\displaystyle\frac{ \alpha c_m }{1+ \alpha c_m }$
theta = alpha * c_m /(1+ alpha * c_m )
Considerando os espa os ocupados la concentração do segundo componente ($[P]$), os espa os vazios associados a la concentração do primeiro componente ($[S]$), e os espa os ocupados associados a la concentração do componente reagido ($[SP]$) e o quociente de concentração ($K$):
Se la fração de cobertura de água ($\theta$) representa a fra o da superf cie ocupada por mol culas:
$[SP] \propto \theta$ - espa os ocupados no gr o
$[S] \propto 1-\theta$ - espa os vazios no gr o, e
$[P] \propto c$ - concentra o de vapor de gua no espa o intergranular
Ent o, pode ser expresso como
$\alpha=\displaystyle\frac{\theta}{(1-\theta)c}$
com la constante de Langmuir ($\alpha$).
Resolvendo para la fração de cobertura de água ($\theta$), podemos obter o grau de cobertura como fun o da press o de vapor de gua:
O diferencial de energia livre de Gibbs ($dG$) com la tensão superficial ($\sigma$), la variação de superfície ($dS$), o volume ($V$) e la variação de pressão ($dp$) pode ser expresso da seguinte forma:
A integra o de o diferencial de energia livre de Gibbs ($dG$) desde o estado em que n o h mol culas de gua no menisco at o estado em que atingem a press o saturada requer duas integrais triviais que resultam em la diferença de energia livre de Gibbs ($\Delta G$):
$\displaystyle\int dG = \Delta G$
e a integra o de todo o la condutividade térmica ($\lambda$):
$\displaystyle\int \sigma dS = \sigma S$
Para integrar $Vdp$, importante lembrar que o volume ($V$) resulta da diferen a entre o volume do l quido $V_l$ e o g s $V_g$:
$\Delta V = V_l - V_g \sim - V$
uma vez que $V_l\ll V_g$.
Al m disso, se considerarmos a equa o do g s ideal com la constante de gás universal ($R_C$)
a terceira integral se torna
$-nRT\displaystyle\int_{p_v}^{p_s}\displaystyle\frac{dp}{p}=-nRT\ln\left(\displaystyle\frac{p_s}{p_v}\right)$
Com essas considera es, la diferença de energia livre de Gibbs ($\Delta G$) pode ser expresso como:
A soma de la diferença de energia livre de Gibbs ($\Delta G$) com la tensão superficial ($\sigma$), la seção ($S$), la pressão de vapor de água insaturada ($p_v$), la pressão de vapor de água saturada ($p_s$), o volume ($V$), o volume molar ($V_m$), la temperatura absoluta ($T$) e la constante de gás universal ($R_C$) igual a:
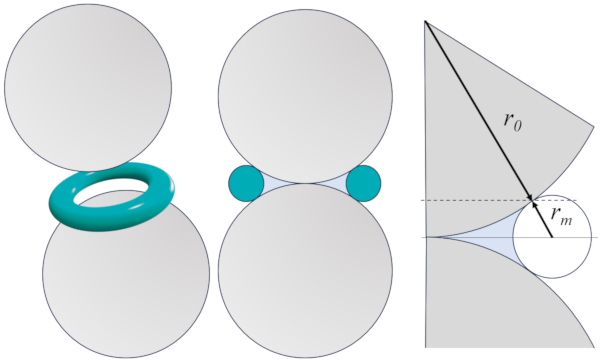
A integral de la seção ($S$) para dois gr os de o raio de um grão genérico ($r_0$) com um menisco de gua de o raio do menisco ($r_m$) no limite $r_m\ll r_0$ dada por:
$S=4\pi \displaystyle\int_0^{r_0r_m/(r_0+r_m)}du[\sqrt{r_0^2+2r_mr_0}-\sqrt{r_m^2-u^2}]\sim 4\pi \sqrt{2r_0r_m^3}$
E para o volume ($V$),
$V=4\pi\displaystyle\int_0^{r_0r_m/(r_0+r_m)}du[r_m^2+r_0(r_m-u)-\sqrt{(r_m(r_m+2r_0)(r_m^2-u^2)}]\sim 2\pi r_0 r_m^2$
Portanto, com a defini o de la umidade relativa ($RH$),
obtemos:
Para que la diferença de energia livre de Gibbs ($\Delta G$) seja minimizado com la tensão superficial ($\sigma$), o raio do menisco ($r_m$), o raio de um grão genérico ($r_0$), la constante de gás universal ($R_C$), la temperatura absoluta ($T$) e la umidade relativa ($RH$), definimos o raio do menisco ($r_m$) como:
Podemos derivar la diferença de energia livre de Gibbs ($\Delta G$) em rela o a o raio do menisco ($r_m$) e igual -lo a zero para encontrar o valor de o raio do menisco ($r_m$) que minimiza la diferença de energia livre de Gibbs ($\Delta G$). Isso nos leva seguinte equa o:
$\displaystyle\frac{\partial\Delta G}{\partial r_m} = 6 \pi \sqrt{2 r_0 r_m } \sigma - 4 \pi r_m r_0 \displaystyle\frac{ R T }{ V_m }\ln\left(\displaystyle\frac{1}{ RH }\right)$
Resolvendo para o raio do menisco ($r_m$), obtemos:
Exemplos
As mol culas de gua em forma de vapor podem ser capturadas pela superf cie dos gr os. Essa absor o ocorre devido s for as intermoleculares.
Por outro lado, devido s oscila es t rmicas, uma mol cula absorvida pode adquirir energia suficiente para se libertar.
Um estado de equil brio alcan ado quando o n mero de part culas absorvidas igual ao n mero que pode ser liberado novamente.
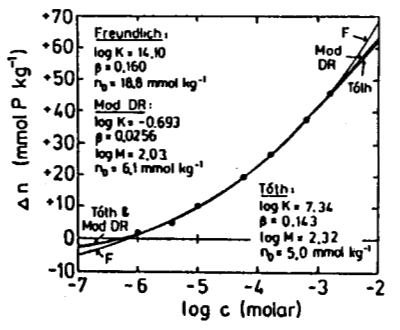
Quando se compara o modelo de Langmuir com sistemas reais, s o observadas discrep ncias significativas. Por esse motivo, surgiram v rios modelos que se baseiam no ajuste de curvas a dados experimentais.
No gr fico apresentado, est o os modelos de Langmuir de uma e duas camadas no lado esquerdo, juntamente com os modelos de Freundlich e Temkin:
[1] "A comparison of the Langmuir, Freundlich and Temkin equations to describe phosphate adsorption properties of soil." (Uma compara o das equa es de Langmuir, Freundlich e Temkin para descrever as propriedades de adsor o de fosfato no solo), Mead, J.A., Aust. J. Soil Res. 19:333-342 (1981).
As mol culas dentro de um l quido experimentam atra es iguais em rela o a todas as suas vizinhas. Isso resulta em que, no geral, as for as exercidas se anulem mutuamente, fazendo com que a mol cula se comporte como uma part cula livre.
No entanto, a situa o diferente para as mol culas na superf cie. Como h mais mol culas no interior do l quido gerando uma for a efetiva para dentro, isso impede que as mol culas na superf cie deixem o l quido.
A for a descrita na se o anterior d origem ao que conhecido como ERROR:tens o superficial. Essa tens o superficial cria uma esp cie de membrana na superf cie, permitindo que alguns insetos se movam sobre ela sem afundar. Por exemplo, a pata da aranha na imagem n o penetra na superf cie, evitando afundar.
A tens o superficial tamb m respons vel pela forma das gotas de gua. A atra o entre as mol culas tende a fazer com que a gota tenha a menor rea de superf cie poss vel, o que significa que ela buscar assumir uma forma esf rica. Isso faz com que um jato de gua tenda a se romper em gotas, e essas gotas tendem a ser esf ricas ou flutuar em torno dessa forma.
A capilaridade faz com que a gua se acumule entre os gr os do solo. Um menisco se forma ao redor da zona de uni o, como mostrado pelas setas vermelhas na imagem abaixo:
la tensão superficial ($\sigma$) gera uma press o interna la pressão de tensão superficial ($p_c$), que depende de ERROR:4962,0, contrabalan ando a press o sobre o menisco gerado la pressão de vapor de água insaturada ($p_v$).
O efeito final do menisco gerar uma for a que une os gr os do solo, proporcionando coes o que crucial para as propriedades mec nicas do solo.
Por outro lado, a mesma tens o dificulta a remo o da gua do solo durante os processos de secagem.
Para ilustrar, considere a constru o de castelos de areia na praia. Se adicionarmos gua demais areia, os meniscos n o se formam (o raio maior que o gr o), e a areia n o mold vel. Por outro lado, medida que o sol seca a areia, a coes o perdida, e o castelo desmorona.
A geometria definida por dois gr os que s o assumidos como esferas de o raio de um grão genérico ($r_0$) em contato em um ponto. Nesta regi o, forma-se uma regi o com gua que, gra as a la tensão superficial ($\sigma$), concentra-se ao redor do ponto de contato e cria um menisco de o raio do menisco ($r_m$) em sua vizinhan a, de maneira semelhante a se existisse um toro imagin rio, como mostrado na imagem abaixo:
&bull: la seção ($S$) corresponde linha do toro imagin rio entre os dois pontos de contato entre o gr o e o toro, que posteriormente deve ser girada em torno de um eixo que passa pelos dois centros dos gr os.
&bull: o volume ($V$) corresponde rea azul, que posteriormente deve ser girada em torno de um eixo que passa pelos dois centros dos gr os.
As mol culas de gua podem ser adsorvidas pela superf cie dos gr os, ou seja, capturadas e retidas por meio de for as intermoleculares.
A quantidade retida depende tanto dessas for as intermoleculares quanto da concentra o ou press o do vapor de gua presente na superf cie.
Em 1918, Langmuir [1] estudou o equil brio entre um g s de part culas associado a la concentração do segundo componente ($[P]$), espa os vazios associados a la concentração do primeiro componente ($[S]$) e espa os ocupados associados a la concentração do componente reagido ($[SP]$):
$S + P\rightleftharpoons SP$
Ele prop s que as concentra es obedecem a uma equa o do tipo:
[1] "The Adsorption of Gases on Plane Surfaces of Glass, Mica, and Platinum" (A adsor o de gases em superf cies planas de vidro, mica e platina) - Irving Langmuir, Journal of the American Chemical Society, Volume 40, Issue 9, p ginas 1361-1403 (1918).
Com base na suposi o de que as concentra es em uma rea o qu mica podem ser comparadas com as 'componentes': as mol culas de gua no ar (la concentração do segundo componente ($[P]$)), os espa os vazios na superf cie do gr o (la concentração do primeiro componente ($[S]$)) e os locais ocupados (la concentração do componente reagido ($[SP]$)), podemos modelar a cobertura do gr o com a rela o em o quociente de concentração ($K$):
Assim, utilizando la concentração molar ($c_m$), la fração de cobertura de água ($\theta$) e la constante de Langmuir ($\alpha$) [1], obtemos o grau de cobertura em fun o da press o de vapor de gua:
O significado f sico da constante de Langmuir um coeficiente de afinidade da superf cie do gr o com a gua. Quanto maior o seu valor, maior a probabilidade de que as mol culas de gua se adiram superf cie.
[1] "The Constitution and Fundamental Properties of Solids and Liquids. Part I. Solids" (A Constitui o e Propriedades Fundamentais de S lidos e L quidos. Parte I. S lidos) - Irving Langmuir, Journal of the American Chemical Society, Volume 38, Issue 11, p ginas 2221-2295 (1916).
A obten o de la fração de cobertura de água ($\theta$) baseada em la concentração de partículas ($c_n$) e, portanto, pode ser expressa em fun o de la pressão de vapor de água insaturada ($p_v$) utilizando la constante de gás universal ($R_C$) e la temperatura absoluta ($T$) por meio da equa o:
Nesse caso, la constante de Langmuir ($\alpha$) pode ser substitu do por la constante de Langmuir ($\alpha_p$) usando a equa o:
Um artigo que descreve como estimar a constante de Langmuir pode ser consultado em [1]. Outro artigo investiga a adsor o de diferentes ons na superf cie dos gr os [2]. Para uma constante de Langmuir ($\alpha$) da ordem de 1000 L/mol, conforme descrito no artigo, la constante de Langmuir ($\alpha_p$) ser aproximadamente 4.1E-4 1/Pa temperatura ambiente.
[1] "Evaluation of thermodynamic parameters of cadmium adsorption on sand from Temkin adsorption isotherm" (Avalia o de par metros termodin micos da adsor o de c dmio em areia a partir da isoterma de adsor o de Temkin), Abdul Satter Ali Khan, Turk J. Chem 36, 437-443 (2012).
[2] "A Comparison of the Langmuir, Freundlich and Temkin Equations to Describe Phosphate Sorption Characteristics of Some Representative Soils of Bangladesh" (Uma compara o das equa es de Langmuir, Freundlich e Temkin para descrever as caracter sticas de sor o de fosfato em alguns solos representativos de Bangladesh), Mohammad Z. Afsar, Sirajul Hoque, K.T. Osman, International Journal of Soil Science 7 (3): 91-99 (2012).
La fração de cobertura de água ($\theta$) calculado com base em la concentração de partículas ($c_n$), o que permite reescrev -lo em termos de la pressão de vapor de água insaturada ($p_v$) usando la constante de gás universal ($R_C$) e la temperatura absoluta ($T$) por meio da equa o:
Neste caso, a equa o para la fração de cobertura de água ($\theta$) pode ser expressa em termos de la pressão de vapor de água insaturada ($p_v$) da seguinte forma:
La pressão ($p$), o volume ($V$), la temperatura absoluta ($T$) e o número de moles ($n$) est o relacionados pela seguinte equa o:
onde la constante de gás universal ($R_C$) tem um valor de 8,314 J/K mol.
O número de moles ($n$) determinado dividindo o volume ($V$) de uma subst ncia pelo seu o volume molar ($V_m$), que corresponde ao peso de um mol da subst ncia.
Portanto, a seguinte rela o pode ser estabelecida:
O volume molar expresso em metros c bicos por mol ($m^3/mol$).
importante observar que o volume molar depende das condi es de press o e temperatura nas quais a subst ncia se encontra, especialmente no caso de um g s, portanto, definido considerando condi es espec ficas.
Em geral, o diferencial de energia livre de Gibbs ($dG$) igual a la entropia ($S$), la variação de temperatura ($dT$), o volume ($V$) e la variação de pressão ($dp$), o que expresso da seguinte forma:
Durante uma mudan a de fase, necess rio considerar a diferen a desta express o entre as duas fases. No entanto, neste caso, la temperatura absoluta ($T$) n o varia, de modo que o termo $SdT$ n o aparece. Por outro lado, ao considerar a varia o dos termos o volume ($V$) e la variação de pressão ($dp$), isso abrange la variação de volume na mudança de fase ($\Delta V$). Por fim, preciso incluir o termo la tensão superficial ($\sigma$) e la variação de superfície ($dS$):
Em geral, o diferencial de energia livre de Gibbs ($dG$) igual a la tensão superficial ($\sigma$), la variação de superfície ($dS$), o volume ($V$) e la variação de pressão ($dp$), o que expresso da seguinte forma:
No entanto, no caso do menisco de gua, la temperatura absoluta ($T$) n o varia, mas a superf cie muda medida que mais mol culas se condensam dentro de o volume ($V$) de gua. Portanto, ao integrar desde a aus ncia de mol culas de gua at atingir o estado de equil brio, obt m-se la diferença de energia livre de Gibbs ($\Delta G$) em termos de la seção ($S$), la pressão de vapor de água insaturada ($p_v$), la pressão de vapor de água saturada ($p_s$), o volume molar ($V_m$) e la constante de gás universal ($R_C$):
La umidade relativa ($RH$) pode ser expresso em termos de la pressão de vapor de água insaturada ($p_v$) e la pressão de vapor de água saturada ($p_s$) como segue:
La diferença de energia livre de Gibbs ($\Delta G$) com la tensão superficial ($\sigma$), la seção ($S$), la pressão de vapor de água insaturada ($p_v$), la pressão de vapor de água saturada ($p_s$), o volume ($V$), o volume molar ($V_m$), la temperatura absoluta ($T$) e la constante de gás universal ($R_C$) igual a:
Para calcular la diferença de energia livre de Gibbs ($\Delta G$), necess rio calcular la tensão superficial ($\sigma$) e o volume ($V$) para o mensico de r dio o raio do menisco ($r_m$), que formado entre os valores supostos de o raio de um grão genérico ($r_0$):
A soma de la diferença de energia livre de Gibbs ($\Delta G$) com la tensão superficial ($\sigma$), o raio do menisco ($r_m$), o raio de um grão genérico ($r_0$), la constante de gás universal ($R_C$), la temperatura absoluta ($T$) e la umidade relativa ($RH$) igual a:
O valor de o raio do menisco ($r_m$) deve ser escolhido de forma a minimizar la diferença de energia livre de Gibbs ($\Delta G$). Para alcan ar isso, podemos derivar la diferença de energia livre de Gibbs ($\Delta G$) em rela o a o raio do menisco ($r_m$), igualar a zero e resolver para o raio do menisco ($r_m$). Isso resulta em:
ID:(374, 0)