Evolución de temperatura
Storyboard 
La evolución de la temperatura en el suelo depende de la temperatura en la superficie y de la temperatura promedio en la profundidad. La conductividad térmica y la capacidad calorífica específica del suelo son los factores determinantes que establecen la profundidad a la cual se alcanza la temperatura media.
ID:(2051, 0)
Evolución de temperatura
Storyboard 
La evolución de la temperatura en el suelo depende de la temperatura en la superficie y de la temperatura promedio en la profundidad. La conductividad térmica y la capacidad calorífica específica del suelo son los factores determinantes que establecen la profundidad a la cual se alcanza la temperatura media.
Variables
Cálculos
Cálculos
Ecuaciones
Dado que la calor transportado ($dQ$) se expresa como una funci n de el largo del conductor ($L$), la sección ($S$), la variación de tiempo ($dt$), la diferencia de temperatura en el conductor ($\Delta T_0$) y la conductividad térmica ($\lambda$) mediante la siguiente ecuaci n:
Con la ecuaci n para la tasa de flujo de calor ($q$) definida como:
En el caso infinitesimal, donde el largo del conductor ($L$) se reduce a una distancia recorrida ($dz$) y la diferencia de temperatura en el conductor ($\Delta T_0$) se convierte en la variación de la temperatura ($dT$), la ecuaci n se simplifica a:
La cantidad de la calor transportado ($dQ$) a trav s de una distancia recorrida ($dz$) puede calcularse utilizando la tasa de flujo de calor ($q$) y la variación de tiempo ($dt$) con la sección ($S$) mediante la siguiente ecuaci n:
$dQ = -\displaystyle\frac{\partial}{\partial z}(q S dt) dz$
Dado que la tasa de flujo de calor ($q$) con la variación de la temperatura ($dT$) y la conductividad térmica ($\lambda$), obtenemos:
Por lo tanto,
$dQ = \displaystyle\frac{\partial}{\partial z}(\lambda \displaystyle\frac{\partial T}{\partial z}) S dz dt$
Por otro lado, podemos relacionar la calor suministrado al liquido o solido ($\Delta Q$) con la masa ($M$), el calor específico ($c$) y la variación de la temperatura ($\Delta T$) mediante la ecuaci n:
En este caso, con la variación del volumen ($\Delta V$), la ecuaci n se convierte en:
$dQ=\rho dV c dT = \rho c S dz dT$
Finalmente, obtenemos:
Como la tasa de flujo de calor ($q$) junto con la conductividad térmica ($\lambda$), la temperatura en el suelo ($T$) y la profundidad ($z$) da como resultado
Para la soluci n de la temperatura en el suelo ($T$) con la profundidad ($z$) y el tiempo ($t$), se utilizan la temperatura media ambiental ($T_m$), la variación anual de la temperatura en el suelo ($\Delta T_s$), la cambio de fase de tiempo ($t_0$), la profundidad media de la variación ($d_m$) y la frecuencia angular anual ($\omega_m$):
Esto se obtiene en la superficie ($z=0$) y sin desplazamiento de fase ($t_0=0$):
La tasa de flujo de calor ($q$) as a function of la conductividad térmica ($\lambda$), la variación anual de la temperatura en el suelo ($\Delta T_s$), la profundidad media de la variación ($d_m$), la frecuencia angular anual ($\omega_m$), el tiempo ($t$), and la cambio de fase de tiempo ($t_0$) is given by:
This represents the total flow passing through the area over the ground and the ground itself. In the first case, the flow is equal to el coeficiente de transmisión ($\alpha$) due to the temperature difference between the environment and the ground surface. For the situation where el tiempo ($t$) is equal to la cambio de fase de tiempo ($t_0$), the flow in the area over the ground is described by:
$\alpha \left(\displaystyle\frac{\Delta T_m}{2}-\displaystyle\frac{\Delta T_s}{2}\right) = \displaystyle\frac{\lambda \Delta T_s}{2 d_m}$
If we solve for la variación anual de la temperatura en el suelo ($\Delta T_s$), we obtain:
Ejemplos
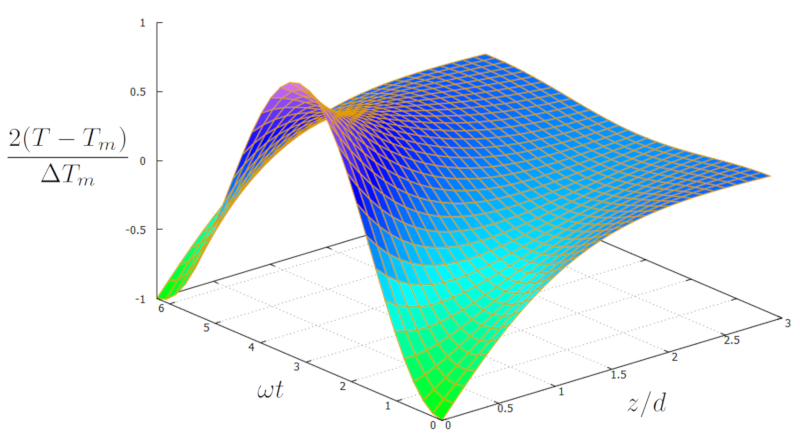
Si graficamos la soluci n para la temperatura en el suelo ($T$) en funci n de la profundidad ($z$) y el tiempo ($t$), utilizando la temperatura media ambiental ($T_m$), la variación anual de la temperatura en el suelo ($\Delta T_s$), la cambio de fase de tiempo ($t_0$), la profundidad media de la variación ($d_m$) y la frecuencia angular anual ($\omega_m$), obtenemos:
Esto nos da una curva que, en la superficie ($z=0$), muestra el m ximo del verano y el m nimo del invierno en temperatura. Luego, la temperatura converge hacia la temperatura promedio a medida que aumenta la profundidad, manteni ndose constante. Adem s, hay un efecto de inercia en el sistema:
La tasa de flujo de calor ($q$) se define en funci n de la calor transportado ($dQ$), la variación de tiempo ($dt$), y la sección ($S$) de la siguiente manera:
Para un conductor con valores de el largo del conductor ($L$) y la sección ($S$), se describe el flujo de la calor transportado ($dQ$) en la variación de tiempo ($dt$) bajo la diferencia de temperatura en el conductor ($\Delta T_0$) y la conductividad térmica ($\lambda$) mediante la siguiente ecuaci n:
En el caso infinitesimal, donde el largo del conductor ($L$) se reduce a una distancia recorrida ($dz$) y la diferencia de temperatura en el conductor ($\Delta T_0$) se convierte en la variación de la temperatura ($dT$), la ecuaci n para la tasa de flujo de calor ($q$) se simplifica a:
[1] "Th orie analytique de la chaleur" (La teor a anal tica del calor), Joseph Fourier, Cambridge University Press (2009) (original 1822)
La definici n de la tasa de flujo de calor ($q$) se realiza utilizando la conductividad térmica ($\lambda$) y la variación de la temperatura ($dT$) en funci n de la distancia recorrida ($dz$) mediante la siguiente ecuaci n:
Al estudiar el flujo de calor, se obtiene la ecuaci n para la temperatura absoluta ($T$) en funci n de la posición a lo largo de un eje ($z$), el tiempo ($t$) y la conductividad térmica ($\lambda$) que se convierte en el calor específico ($c$). La ecuaci n para la densidad ($\rho$) se simplifica a:
Si consideramos que la temperatura en la superficie experimenta fluctuaciones diarias r pidas y una lenta variaci n anual, y que la inercia del sistema impide que las fluctuaciones diarias afecten el suelo, podemos estimar la la temperatura en el suelo ($T$) en funci n de la profundidad ($z$) y el tiempo ($t$) a lo largo del a o como la soluci n de la siguiente ecuaci n:
donde la conductividad térmica ($\lambda$), el calor específico ($c$) y la densidad ($\rho$). Por lo tanto, la soluci n se obtiene con la temperatura media ambiental ($T_m$), la variación anual de la temperatura en el suelo ($\Delta T_s$), la profundidad media de la variación ($d_m$), la cambio de fase de tiempo ($t_0$) y la frecuencia angular anual ($\omega_m$) de la siguiente manera:
El valor de la cambio de fase de tiempo ($t_0$) se suele emplear para ajustar la soluci n al hemisferio correspondiente. En este sentido, en el hemisferio norte, este desfase es casi nulo, mientras que en el hemisferio sur es de aproximadamente medio a o.
La soluci n para la temperatura en el suelo ($T$) en la profundidad ($z$) y el tiempo ($t$) se obtiene utilizando la temperatura media ambiental ($T_m$), la variación anual de la temperatura en el suelo ($\Delta T_s$), la cambio de fase de tiempo ($t_0$), la profundidad media de la variación ($d_m$) y la frecuencia angular anual ($\omega_m$), lo que resulta en:
Esta soluci n resuelve la ecuaci n de conducci n cuando la profundidad media de la variación ($d_m$) es igual a la conductividad térmica ($\lambda$), el calor específico ($c$) y la densidad ($\rho$) mediante:
Para resolver la temperatura en el suelo ($T$) en la profundidad ($z$) y el tiempo ($t$), utilizamos la temperatura media ambiental ($T_m$), la variación anual de la temperatura en el suelo ($\Delta T_s$), la cambio de fase de tiempo ($t_0$), la profundidad media de la variación ($d_m$) y la frecuencia angular anual ($\omega_m$), lo que resulta en:
Esto nos permite calcular el flujo de calor en la superficie en el caso en que la cambio de fase de tiempo ($t_0$) se considere nulo y con la conductividad térmica ($\lambda$) y la profundidad media de la variación ($d_m$) mediante:
La variación anual de la temperatura en el ambiente ($\Delta T_m$) esta por lo general dado por la situaci n climatica a lo largo del a o. Sin embargo la variación anual de la temperatura en el suelo ($\Delta T_s$) es desconocido y depende del suelo en si y de el coeficiente de transmisión ($\alpha$).
Como el la tasa de flujo de calor ($q$) con la conductividad térmica ($\lambda$), la profundidad media de la variación ($d_m$), la frecuencia angular anual ($\omega_m$) esta dado para todo el tiempo ($t$) mediante
se puede calcular el flujo por la zona de la superficie y mostrar que la variación anual de la temperatura en el ambiente ($\Delta T_m$) es:
ID:(2051, 0)