Evolution de la température
Storyboard 
La température dans le sol évolue en fonction de la température en surface et de la température moyenne en profondeur. La conductivité thermique et la capacité calorifique spécifique du sol déterminent la profondeur à laquelle la température moyenne est atteinte.
ID:(2051, 0)
Evolution de la température
Storyboard 
La température dans le sol évolue en fonction de la température en surface et de la température moyenne en profondeur. La conductivité thermique et la capacité calorifique spécifique du sol déterminent la profondeur à laquelle la température moyenne est atteinte.
Variables
Calculs
Calculs
Équations
tant donn que a chaleur transportée ($dQ$) est une fonction de le longueur du pilote ($L$), a section ($S$), a variation temporelle ($dt$), a différence de température dans le conducteur ($\Delta T_0$) et a conductivité thermique ($\lambda$) selon l' quation suivante :
Avec l' quation pour a débit de chaleur ($q$) d finie comme suit :
Dans le cas infinit simal, o le longueur du pilote ($L$) se r duit une distance parcourue ($dz$) et a différence de température dans le conducteur ($\Delta T_0$) devient a variation de température ($dT$), l' quation se simplifie :
La quantit de a chaleur transportée ($dQ$) travers une distance parcourue ($dz$) peut tre calcul e en utilisant a débit de chaleur ($q$) et a variation temporelle ($dt$) avec a section ($S$) gr ce l' quation suivante :
$dQ = -\displaystyle\frac{\partial}{\partial z}(q S dt) dz$
Puisque a débit de chaleur ($q$) avec a variation de température ($dT$) et a conductivité thermique ($\lambda$) est d fini comme suit :
Par cons quent,
$dQ = \displaystyle\frac{\partial}{\partial z}(\lambda \displaystyle\frac{\partial T}{\partial z}) S dz dt$
D'autre part, nous pouvons relier a chaleur fournie au liquide ou au solide ($\Delta Q$) avec a masse ($M$), le chaleur spécifique ($c$) et a variation de température ($\Delta T$) gr ce l' quation suivante :
Dans ce cas, avec a variation de volume ($\Delta V$), l' quation devient :
$dQ=\rho dV c dT = \rho c S dz dT$
Et enfin, nous obtenons :
Comme a débit de chaleur ($q$) en combinaison avec a conductivité thermique ($\lambda$), a température du sol ($T$) et a profondeur ($z$) donne comme r sultat
Pour la solution de a température du sol ($T$) avec a profondeur ($z$) et le temps ($t$), nous utilisons a température ambiante moyenne ($T_m$), a variation annuelle de la température du sol ($\Delta T_s$), a changement de phase temporelle ($t_0$), a profondeur moyenne de variation ($d_m$) et a profondeur moyenne de variation ($\omega_m$) :
Cela est obtenu la surface ($z=0$) et sans d calage de phase ($t_0=0$) :
A débit de chaleur ($q$) en fonction de a conductivité thermique ($\lambda$), a variation annuelle de la température du sol ($\Delta T_s$), a profondeur moyenne de variation ($d_m$), a profondeur moyenne de variation ($\omega_m$), le temps ($t$) et a changement de phase temporelle ($t_0$) est repr sent par :
Ceci repr sente le flux total passant travers la zone au-dessus du sol et le sol lui-m me. Dans le premier cas, le flux est gal le coefficient de transmission ($\alpha$) en raison de la diff rence de temp rature entre l'environnement et la surface du sol. Pour la situation o le temps ($t$) est gal a changement de phase temporelle ($t_0$), le flux dans la zone au-dessus du sol peut tre d crit comme suit :
$\alpha \left(\displaystyle\frac{\Delta T_m}{2}-\displaystyle\frac{\Delta T_s}{2}\right) = \displaystyle\frac{\lambda \Delta T_s}{2 d_m}$
En r solvant pour a variation annuelle de la température du sol ($\Delta T_s$), nous obtenons :
Exemples
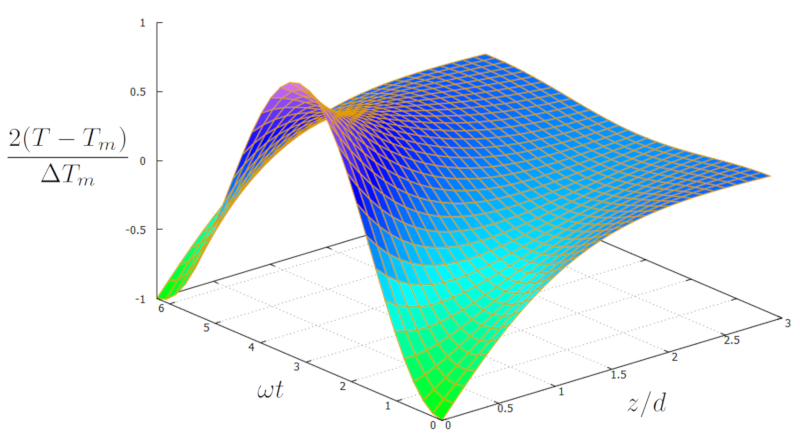
Si nous repr sentons graphiquement la solution pour a température du sol ($T$) en fonction de a profondeur ($z$) et le temps ($t$) en utilisant a température ambiante moyenne ($T_m$), a variation annuelle de la température du sol ($\Delta T_s$), a changement de phase temporelle ($t_0$), a profondeur moyenne de variation ($d_m$) et a profondeur moyenne de variation ($\omega_m$), le r sultat est le suivant :
Cela donne une courbe qui, la surface ($z=0$), montre le maximum de l' t et le minimum de l'hiver en termes de temp rature. La temp rature converge ensuite vers la temp rature moyenne avec la profondeur, restant constante. De plus, il y a un effet d'inertie dans le syst me :
A débit de chaleur ($q$) est d fini en fonction de a chaleur transportée ($dQ$), a variation temporelle ($dt$), et a section ($S$) comme suit :
Pour un conducteur avec les valeurs de le longueur du pilote ($L$) et a section ($S$), le flux de a chaleur transportée ($dQ$) est d crit sous a variation temporelle ($dt$) et a conductivité thermique ($\lambda$) comme suit :
Dans le cas infinit simal, o le longueur du pilote ($L$) se r duit une distance parcourue ($dz$) et a différence de température dans le conducteur ($\Delta T_0$) devient a variation de température ($dT$), l' quation pour a débit de chaleur ($q$) se simplifie :
[1] "Th orie analytique de la chaleur" (La Th orie Analytique de la Chaleur), Joseph Fourier, Cambridge University Press (2009) (original de 1822)
La d finition de a débit de chaleur ($q$) est tablie en utilisant a conductivité thermique ($\lambda$) et a variation de température ($dT$) en fonction de a distance parcourue ($dz$) travers l' quation suivante :
En tudiant le flux de chaleur, nous obtenons l' quation pour a température absolue ($T$) en fonction de a positionner le long d'un axe ($z$), le temps ($t$) et a conductivité thermique ($\lambda$), qui devient le chaleur spécifique ($c$). L' quation pour a densité ($\rho$) se simplifie :
Si l'on consid re que la temp rature de la surface subit des fluctuations quotidiennes rapides ainsi qu'une variation annuelle lente, et que l'inertie du syst me emp che les fluctuations quotidiennes d'affecter le sol, nous pouvons estimer la a température du sol ($T$) en fonction de a profondeur ($z$) et de le temps ($t$) tout au long de l'ann e en tant que solution de l' quation suivante :
o a conductivité thermique ($\lambda$), le chaleur spécifique ($c$) et a densité ($\rho$). Par cons quent, la solution est obtenue avec a température ambiante moyenne ($T_m$), a variation annuelle de la température du sol ($\Delta T_s$), a profondeur moyenne de variation ($d_m$), a changement de phase temporelle ($t_0$) et a profondeur moyenne de variation ($\omega_m$) de la mani re suivante :
La valeur de a changement de phase temporelle ($t_0$) est g n ralement utilis e pour ajuster la solution l'h misph re correspondant. cet gard, dans l'h misph re nord, ce d calage est presque nul, tandis que dans l'h misph re sud, il est d'environ un demi-ann e.
La solution pour a température du sol ($T$) dans a profondeur ($z$) et le temps ($t$) est obtenue en utilisant a température ambiante moyenne ($T_m$), a variation annuelle de la température du sol ($\Delta T_s$), a changement de phase temporelle ($t_0$), a profondeur moyenne de variation ($d_m$), et a profondeur moyenne de variation ($\omega_m$), ce qui donne :
Cette solution r sout l' quation de conduction lorsque a profondeur moyenne de variation ($d_m$) est gal a conductivité thermique ($\lambda$), le chaleur spécifique ($c$), et a densité ($\rho$) travers :
Pour r soudre a température du sol ($T$) dans a profondeur ($z$) et le temps ($t$), nous utilisons a température ambiante moyenne ($T_m$), a variation annuelle de la température du sol ($\Delta T_s$), a changement de phase temporelle ($t_0$), a profondeur moyenne de variation ($d_m$), et a profondeur moyenne de variation ($\omega_m$), ce qui donne :
Cela nous permet de calculer le flux de chaleur la surface dans le cas o a changement de phase temporelle ($t_0$) est suppos tre nul et avec a conductivité thermique ($\lambda$) et a profondeur moyenne de variation ($d_m$) en utilisant :
Pour r soudre a température du sol ($T$) dans a profondeur ($z$) et le temps ($t$), nous utilisons a température ambiante moyenne ($T_m$), a variation annuelle de la température du sol ($\Delta T_s$), a changement de phase temporelle ($t_0$), a profondeur moyenne de variation ($d_m$), et a profondeur moyenne de variation ($\omega_m$), ce qui donne :
Cela nous permet de calculer le flux de chaleur la surface dans le cas o a changement de phase temporelle ($t_0$) est suppos tre nul et avec a conductivité thermique ($\lambda$) et a profondeur moyenne de variation ($d_m$) en utilisant :
ID:(2051, 0)