Evolução da temperatura
Storyboard 
A temperatura no solo evolui com base na temperatura na superfície e na temperatura média na profundidade. A condutividade térmica e a capacidade calorífica específica do solo determinam a profundidade na qual a temperatura média é alcançada.
ID:(2051, 0)
Evolução da temperatura
Storyboard 
A temperatura no solo evolui com base na temperatura na superfície e na temperatura média na profundidade. A condutividade térmica e a capacidade calorífica específica do solo determinam a profundidade na qual a temperatura média é alcançada.
Variáveis
Cálculos
Cálculos
Equações
Uma vez que la calor transportado ($dQ$) uma fun o de o comprimento do conductor ($L$), la seção ($S$), la variação de tempo ($dt$), la diferença de temperatura no condutor ($\Delta T_0$) e la condutividade térmica ($\lambda$), de acordo com a seguinte equa o:
Com a equa o para la taxa de fluxo de calor ($q$) definida como:
No caso infinitesimal, onde o comprimento do conductor ($L$) se reduz a uma distância percorrida ($dz$) e la diferença de temperatura no condutor ($\Delta T_0$) se torna la variação de temperatura ($dT$), a equa o se simplifica para:
A quantidade de la calor transportado ($dQ$) atrav s de uma distância percorrida ($dz$) pode ser calculada usando la taxa de fluxo de calor ($q$) e la variação de tempo ($dt$) com la seção ($S$) atrav s da seguinte equa o:
$dQ = -\displaystyle\frac{\partial}{\partial z}(q S dt) dz$
Uma vez que la taxa de fluxo de calor ($q$) com la variação de temperatura ($dT$) e la condutividade térmica ($\lambda$) definido como:
Portanto,
$dQ = \displaystyle\frac{\partial}{\partial z}(\lambda \displaystyle\frac{\partial T}{\partial z}) S dz dt$
Por outro lado, podemos relacionar la calor fornecido ao líquido ou sólido ($\Delta Q$) com la massa ($M$), o calor específico ($c$) e la variação de temperatura ($\Delta T$) atrav s da seguinte equa o:
Neste caso, com la variação de volume ($\Delta V$), a equa o se torna:
$dQ=\rho dV c dT = \rho c S dz dT$
E finalmente, obtemos:
Como la taxa de fluxo de calor ($q$) junto com la condutividade térmica ($\lambda$), la temperatura do solo ($T$) e la profundidade ($z$) resulta em
Para a solu o de la temperatura do solo ($T$) com la profundidade ($z$) e o tempo ($t$), utilizamos la temperatura ambiente média ($T_m$), la variação anual da temperatura do solo ($\Delta T_s$), la mudança de fase de tempo ($t_0$), la profundidade média de variação ($d_m$) e la profundidade média de variação ($\omega_m$):
Isso obtido na superf cie ($z=0$) e sem deslocamento de fase ($t_0=0$):
La taxa de fluxo de calor ($q$) como uma fun o de la condutividade térmica ($\lambda$), la variação anual da temperatura do solo ($\Delta T_s$), la profundidade média de variação ($d_m$), la profundidade média de variação ($\omega_m$), o tempo ($t$) e la mudança de fase de tempo ($t_0$) representado por:
Isso representa o fluxo total que passa pela rea acima do solo e pelo pr prio solo. No primeiro caso, o fluxo igual a o coeficiente de transmissão ($\alpha$) devido diferen a de temperatura entre o ambiente e a superf cie do solo. Para a situa o em que o tempo ($t$) igual a la mudança de fase de tempo ($t_0$), o fluxo na rea acima do solo pode ser descrito como:
$\alpha \left(\displaystyle\frac{\Delta T_m}{2}-\displaystyle\frac{\Delta T_s}{2}\right) = \displaystyle\frac{\lambda \Delta T_s}{2 d_m}$
Resolvendo para la variação anual da temperatura do solo ($\Delta T_s$), obtemos:
Exemplos
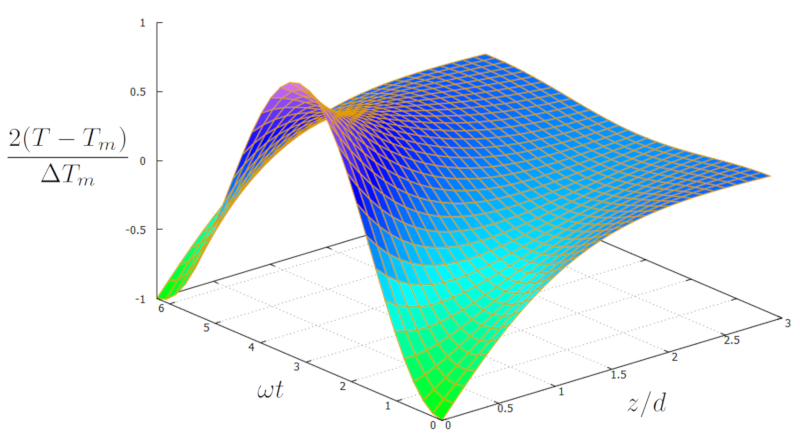
Se plotarmos a solu o para la temperatura do solo ($T$) em fun o de la profundidade ($z$) e o tempo ($t$) usando la temperatura ambiente média ($T_m$), la variação anual da temperatura do solo ($\Delta T_s$), la mudança de fase de tempo ($t_0$), la profundidade média de variação ($d_m$) e la profundidade média de variação ($\omega_m$), o resultado :
Isso produz uma curva que, na superf cie ($z=0$), exibe o m ximo do ver o e o m nimo do inverno em temperatura. A temperatura ent o converge para a temperatura m dia com a profundidade, mantendo-se constante. Al m disso, h um efeito de in rcia no sistema:
La taxa de fluxo de calor ($q$) definido em termos de la calor transportado ($dQ$), la variação de tempo ($dt$) e la seção ($S$) da seguinte forma:
Para um condutor com valores de o comprimento do conductor ($L$) e la seção ($S$), o fluxo de la calor transportado ($dQ$) descrito sob la variação de tempo ($dt$) e la condutividade térmica ($\lambda$) da seguinte forma:
No caso infinitesimal, onde o comprimento do conductor ($L$) se reduz a uma distância percorrida ($dz$) e la diferença de temperatura no condutor ($\Delta T_0$) se torna la variação de temperatura ($dT$), a equa o para la taxa de fluxo de calor ($q$) se simplifica para:
[1] "Th orie analytique de la chaleur" (A Teoria Anal tica do Calor), Joseph Fourier, Cambridge University Press (2009) (original de 1822)
A defini o de la taxa de fluxo de calor ($q$) estabelecida utilizando la condutividade térmica ($\lambda$) e la variação de temperatura ($dT$) como fun o de la distância percorrida ($dz$) atrav s da seguinte equa o:
Ao estudar o fluxo de calor, obtemos a equa o para la temperatura absoluta ($T$) como fun o de la posição ao longo de um eixo ($z$), o tempo ($t$) e la condutividade térmica ($\lambda$), que se torna o calor específico ($c$). A equa o para la densidade ($\rho$) se simplifica para:
Se considerarmos que a temperatura da superf cie sofre flutua es di rias r pidas e uma varia o anual lenta, e que a in rcia do sistema impede que as flutua es di rias afetem o solo, podemos estimar a la temperatura do solo ($T$) como fun o de la profundidade ($z$) e o tempo ($t$) ao longo do ano como a solu o da seguinte equa o:
onde la condutividade térmica ($\lambda$), o calor específico ($c$) e la densidade ($\rho$). Portanto, a solu o obtida com la temperatura ambiente média ($T_m$), la variação anual da temperatura do solo ($\Delta T_s$), la profundidade média de variação ($d_m$), la mudança de fase de tempo ($t_0$) e la profundidade média de variação ($\omega_m$) da seguinte maneira:
O valor de la mudança de fase de tempo ($t_0$) geralmente usado para ajustar a solu o ao hemisf rio correspondente. Nesse sentido, no hemisf rio norte, esse desfasamento quase nulo, enquanto no hemisf rio sul aproximadamente meio ano.
A solu o para la temperatura do solo ($T$) em la profundidade ($z$) e o tempo ($t$) obtida utilizando la temperatura ambiente média ($T_m$), la variação anual da temperatura do solo ($\Delta T_s$), la mudança de fase de tempo ($t_0$), la profundidade média de variação ($d_m$) e la profundidade média de variação ($\omega_m$), resultando em:
Esta solu o resolve a equa o de condu o quando la profundidade média de variação ($d_m$) igual a la condutividade térmica ($\lambda$), o calor específico ($c$) e la densidade ($\rho$) atrav s de:
Para resolver la temperatura do solo ($T$) em la profundidade ($z$) e o tempo ($t$), utilizamos la temperatura ambiente média ($T_m$), la variação anual da temperatura do solo ($\Delta T_s$), la mudança de fase de tempo ($t_0$), la profundidade média de variação ($d_m$) e la profundidade média de variação ($\omega_m$), resultando em:
Isso nos permite calcular o fluxo de calor na superf cie no caso em que la mudança de fase de tempo ($t_0$) considerado nulo e com la condutividade térmica ($\lambda$) e la profundidade média de variação ($d_m$) usando:
Para resolver la temperatura do solo ($T$) em la profundidade ($z$) e o tempo ($t$), utilizamos la temperatura ambiente média ($T_m$), la variação anual da temperatura do solo ($\Delta T_s$), la mudança de fase de tempo ($t_0$), la profundidade média de variação ($d_m$) e la profundidade média de variação ($\omega_m$), resultando em:
Isso nos permite calcular o fluxo de calor na superf cie no caso em que la mudança de fase de tempo ($t_0$) considerado nulo e com la condutividade térmica ($\lambda$) e la profundidade média de variação ($d_m$) usando:
ID:(2051, 0)