Utilisateur:
Transport de chaleur
Storyboard 
L'humidité du sol dépend de sa température, il est donc important de calculer cette distribution. Cette relation est déterminée par le flux de chaleur échangé avec la surface du sol.
ID:(2054, 0)
Mécanisme de transport de chaleur
Image
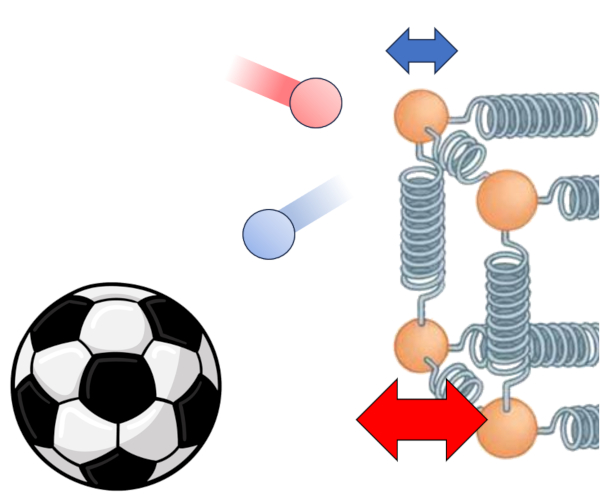
Dans le cas d'un solide, et de manière similaire pour un liquide, nous pouvons décrire le système comme une structure d'atomes liés par quelque chose qui se comporte comme un ressort. Lorsque les deux extrémités ont des températures de une différence de température dans le conducteur ($\Delta T_0$), avec a température de la surface intérieure ($T_{is}$) et a température de la surface extérieure ($T_{es}$) :
| $ \Delta T_0 = T_{is} - T_{es} $ |
La différence de température implique que les atomes aux extrémités oscillent de manière différente ; les atomes dans la zone à haute température auront une amplitude plus grande dans leurs oscillations par rapport aux atomes dans la zone à basse température.
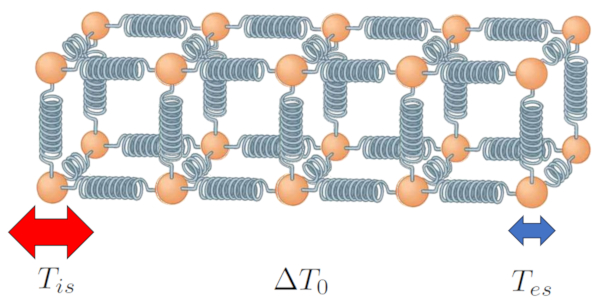
Cependant, cette différence conduira progressivement à ce que toute la chaîne oscille de telle manière qu'à la fin, l'amplitude variera le long du chemin, depuis les valeurs les plus élevées là où la température est également plus élevée, jusqu'aux valeurs les plus basses dans la zone à basse température.
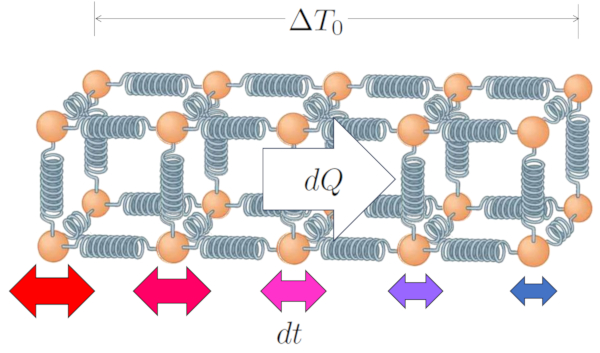
De cette manière, a différence de température dans le conducteur ($\Delta T_0$) mène à Une chaleur transportée ($dQ$) en une variation temporelle ($dt$).
ID:(15234, 0)
Géométrie et dépendance aux matériaux
Noter
L'un des facteurs clés déterminant la quantité de chaleur pouvant être conduite à travers un solide ou un liquide est sa section transversale, c'est-à-dire la quantité de chaînes d'atomes disponibles. Plus nous avons de ces chaînes, plus notre capacité de transport de chaleur est grande.
Cependant, la longueur de ces chaînes peut être contreproductive. À mesure que la chaîne de ressorts devient plus longue, notre capacité à transmettre la chaleur diminue, car de plus en plus d'atomes doivent ajuster leurs amplitudes d'oscillation.
Si nous représentons cela avec a section ($S$) et le longueur du pilote ($L$), le diagramme prend la forme suivante :
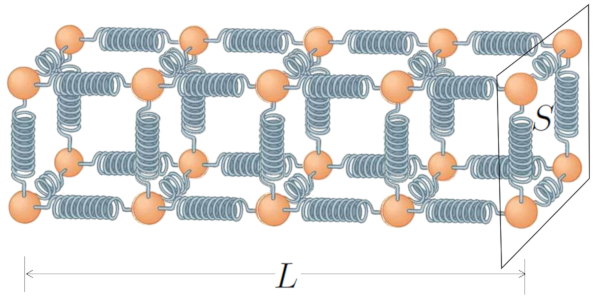
Enfin, la capacité du milieu et du matériau à transporter la chaleur, décrite par les coefficients le coefficient de transmission interne ($\alpha_i$) et le coefficient de transmission externe ($\alpha_e$), ainsi que a conductivité thermique ($\lambda$), explique comment la chaleur se déplace en réponse à A différence de température ($\Delta T$) créée par la différence entre a température intérieure ($T_i$) et a température extérieure ($T_e$) :
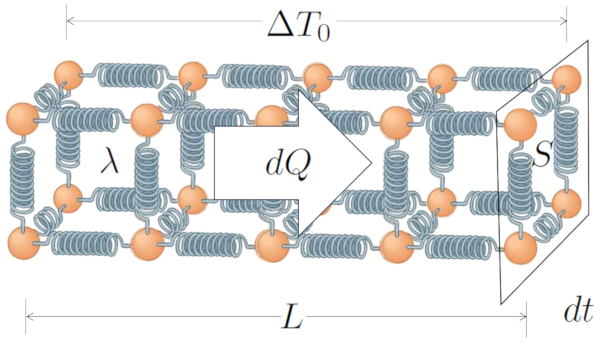
Ceci est calculé comme suit :
| $ \Delta T = T_i - T_e $ |
ID:(15235, 0)
Conduction thermique
Citation
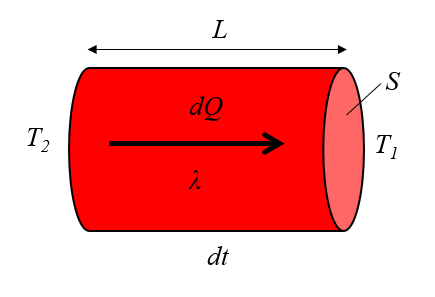
La conduction thermique a été modélisée pour la première fois par Jean Baptiste Joseph Fourier [1], qui a établi que a débit de chaleur ($q$), défini par a chaleur transportée ($dQ$), a variation temporelle ($dt$) et a section ($S$), est exprimée par :
| $ q \equiv \displaystyle\frac{1}{ S }\displaystyle\frac{ dQ }{ dt }$ |
Cette théorie est également liée à A section ($S$), le longueur du pilote ($L$), a différence de température dans le conducteur ($\Delta T_0$) et a conductivité thermique ($\lambda$), comme illustré dans :
| $ q = \displaystyle\frac{ \lambda }{ L } \Delta T_0 $ |
et est décrite avec le diagramme suivant :
[1] "Théorie Analytique de la Chaleur", Jean Baptiste Joseph Fourier, 1822.
ID:(15236, 0)
Dépendance du transfert de chaleur sur la géométrie du conducteur
Exercer
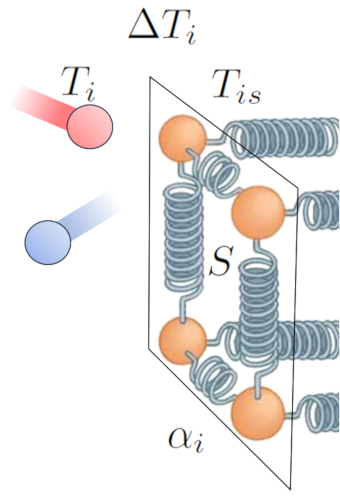
Le principal moteur du transfert de chaleur d'un milieu à un conducteur est la différence de température. Dans le milieu a température intérieure ($T_i$), les particules ont plus d'énergie, et lorsqu'elles entrent en collision avec celles du conducteur à Une température de la surface intérieure ($T_{is}$), elles ont tendance à augmenter l'énergie de ce dernier. Cette interaction peut être représentée comme suit :
Au-delà de la température en elle-même, le flux de chaleur dépend de a différence de température à l'interface interne ($\Delta T_i$) :
| $ \Delta T_i = T_i - T_{is} $ |
Un autre facteur clé est le nombre d'atomes dont l'amplitude d'oscillation peut être augmentée, ce qui dépend de a section ($S$). Enfin, nous devons également prendre en compte les propriétés de surface, décrites par le coefficient de transmission interne ($\alpha_i$), qui correspondent à la relation entre la chaleur transmise, la surface, la différence de température et le temps écoulé :
ID:(15237, 0)
Calcul de la transmission thermique au conducteur
Équation
De cette manière, nous établissons une relation qui nous permet de calculer a débit de chaleur ($q$) en fonction de a différence de température à l'interface interne ($\Delta T_i$) et le coefficient de transmission interne ($\alpha_i$) :
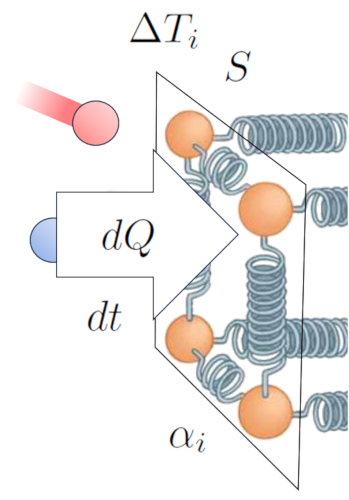
Cela peut s'exprimer mathématiquement comme suit :
| $ q = \alpha_i \Delta T_i $ |
ID:(15238, 0)
Dépendance du transfert de chaleur sur la géométrie du conducteur
Script
Le principal moteur du transfert de chaleur d'un conducteur à un milieu est la différence de température. Lorsque a température de la surface extérieure ($T_{es}$), les particules ont plus d'énergie et oscillent avec une amplitude plus grande en interagissant avec les atomes et les molécules du milieu à Une température extérieure ($T_e$). Cela a tendance à augmenter l'énergie de ces derniers. Cette interaction peut être représentée comme suit :
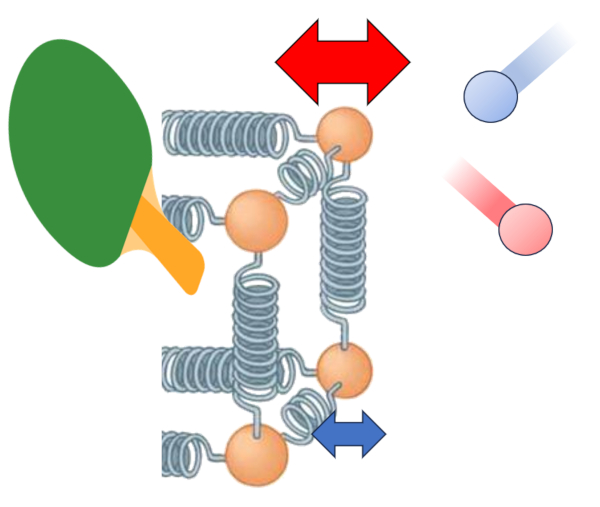
Au-delà de la température, le flux de chaleur dépend de a différence de température à l'interface externe ($\Delta T_e$).
| $ \Delta T_e = T_{es} - T_e $ |
Un autre facteur clé est le nombre d'atomes qui peuvent avoir leur amplitude d'oscillation augmentée, ce qui dépend de a section ($S$). Enfin, nous devons également tenir compte des propriétés de surface, représentées par le coefficient de transmission externe ($\alpha_e$), qui correspondent à la relation entre la chaleur transférée, la surface, la différence de température et le temps écoulé :
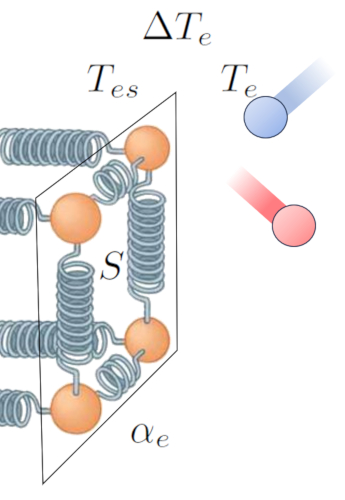
ID:(15239, 0)
Transfert de chaleur du conducteur
Variable
De cette manière, nous établissons une relation qui nous permet de calculer a débit de chaleur ($q$) en fonction de a différence de température à l'interface externe ($\Delta T_e$) et le coefficient de transmission externe ($\alpha_e$) :
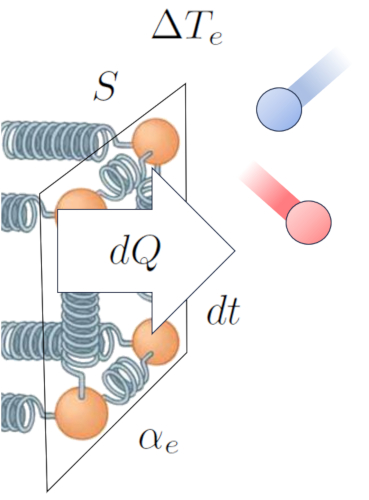
Cela peut être exprimé mathématiquement comme suit :
| $ q = \alpha_e \Delta T_e $ |
ID:(15240, 0)
Transport de chaleur total par un conducteur
Audio
Les modèles de transfert de chaleur et de conduction suggèrent qu'il est possible de développer une relation qui intègre ces trois mécanismes ensemble. Cette équation devrait prendre en compte a chaleur transportée ($dQ$), a variation temporelle ($dt$), a différence de température ($\Delta T$), a section ($S$) et le coefficient de transport total (supports multiples, deux interfaces) ($k$) :
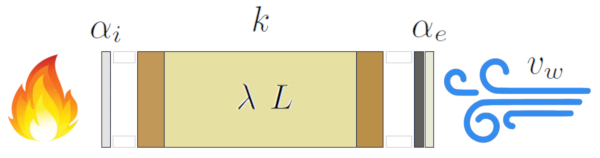
Mathématiquement, cela peut s'exprimer comme suit :
| $ q = k \Delta T $ |
ID:(15241, 0)
Dépendance du coefficient de transfert sur la vitesse du milieu
Video
L'un des effets du transfert de chaleur d'un conducteur à un milieu externe est le réchauffement du milieu près de l'interface, créant une zone d'interférence dans la transmission. Cela diminue l'efficacité du transfert et tend à former une couche isolante qui réduit le flux d'énergie.
Cependant, cet effet peut changer en présence de vent. Le vent peut éliminer la couche d'atomes et de molécules à haute température, améliorant ainsi l'efficacité du transfert de chaleur. Cela suggère que le coefficient de transmission ($\alpha$) est influencé par a vitesse moyenne ($v_m$) [1,2] :
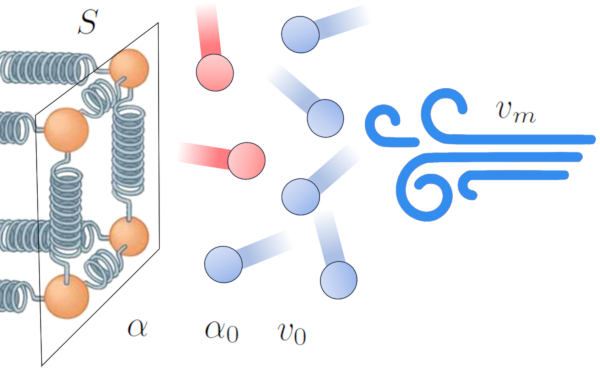
Dans ce contexte, nous modélisons la relation en fonction de ERROR:9844,0 et d'un facteur de référence de le vitesse de référence du support ($v_0$).
La relation mathématique qui décrit ce phénomène pour un gaz avec le coefficient de transmission dans les gaz, en fonction de la vitesse ($\alpha_{gv}$), a vitesse moyenne ($v_m$), le coefficient de transmission dans les gaz, indépendant de la vitesse ($\alpha_{g0}$) et le coefficient de transmission Facteur de vitesse du gaz ($v_{g0}$) est :
| $ \alpha_{gv} = \alpha_{g0} \left(1+\displaystyle\frac{ v_m }{ v_{g0} }\right)$ |
Et pour un liquide avec le coefficient de transmission dans le liquide, en fonction de la vitesse ($\alpha_{wv}$), a vitesse moyenne ($v_m$), le coefficient de transmission dans le liquide, indépendant de la vitesse ($\alpha_{w0}$) et le coefficient de transmission Facteur de vitesse du liquide ($v_{w0}$) :
| $ \alpha_{wv} = \alpha_{w0} \left(1+\sqrt{\displaystyle\frac{ v_m }{ v_{w0} }}\right)$ |
Cela illustre comment le vent peut influencer de manière significative l'efficacité du transfert de chaleur entre un conducteur et un milieu externe.
[1] "Über Flüssigkeitsbewegung bei sehr kleiner Reibung" (Sur le mouvement des fluides avec très peu de friction), Ludwig Prandtl, 1904
[2] "Die Abhängigkeit der Wärmeübergangszahl von der Rohrlänge" (La dépendance du coefficient de transfert de chaleur à la longueur du tuyau), Wilhelm Nusselt, 1910
ID:(3620, 0)
Transport de chaleur
Storyboard
L'humidité du sol dépend de sa température, il est donc important de calculer cette distribution. Cette relation est déterminée par le flux de chaleur échangé avec la surface du sol.
Variables
Calculs
à 
,
puis, sélectionnez la variable: 
à 
Calculs
Variable
Donnée
Calculer
Cible :
Équation
À utiliser
Équations
Avec a différence de température à l'interface interne ($\Delta T_i$), a différence de température dans le conducteur ($\Delta T_0$), a différence de température à l'interface externe ($\Delta T_e$) et a différence de température ($\Delta T$), nous obtenons
qui peut tre r crit avec a chaleur transportée ($dQ$), a variation temporelle ($dt$), a section ($S$)
et avec a conductivité thermique ($\lambda$) et le longueur du pilote ($L$)
comme
$\Delta T_i + \Delta T_0 + \Delta T_e = \displaystyle\frac{1}{S} \displaystyle\frac{dQ}{dt} \left(\displaystyle\frac{1}{\alpha_i} + \displaystyle\frac{1}{\alpha_e} + \displaystyle\frac{L}{\lambda}\right)$
nous pouvons donc d finir un coefficient combin comme
Avec a différence de température à l'interface interne ($\Delta T_i$), a différence de température dans le conducteur ($\Delta T_0$), a différence de température à l'interface externe ($\Delta T_e$), et a différence de température ($\Delta T$), nous obtenons
qui peut tre r crit avec a chaleur transportée ($dQ$), a variation temporelle ($dt$), a section ($S$)
et avec a conductivité thermique ($\lambda$) et le longueur du pilote ($L$)
et
comme
$\Delta T = \Delta T_i + \Delta T_0 + \Delta T_e = \displaystyle\frac{1}{S} \frac{dQ}{dt} \left(\displaystyle\frac{1}{\alpha_i} + \displaystyle\frac{1}{\alpha_e} + \displaystyle\frac{L}{\lambda}\right) = \displaystyle\frac{1}{Sk} \displaystyle\frac{dQ}{dt}$
aboutissant
Avec a chaleur transportée ($dQ$), a variation temporelle ($dt$), a section ($S$), a différence de température ($\Delta T$) et le coefficient de transport total (supports multiples, deux interfaces) ($k$), nous avons
ce qui, avec le coefficient de transmission interne ($\alpha_i$) et a différence de température à l'interface interne ($\Delta T_i$)
aboutit
$k\Delta T = \alpha_i \Delta T_i$
et avec a température intérieure ($T_i$) et a température de la surface intérieure ($T_{is}$) et
aboutit
Avec a chaleur transportée ($dQ$), a variation temporelle ($dt$), a section ($S$), a différence de température ($\Delta T$) et le coefficient de transport total (supports multiples, deux interfaces) ($k$), nous obtenons
ce qui, avec le coefficient de transmission externe ($\alpha_e$) et a différence de température à l'interface externe ($\Delta T_e$)
aboutit
$k\Delta T = \alpha_e \Delta T_e$
et avec a température extérieure ($T_e$) et a température de la surface extérieure ($T_{es}$) et
aboutit
Exemples
Dans le cas d'un solide, et de mani re similaire pour un liquide, nous pouvons d crire le syst me comme une structure d'atomes li s par quelque chose qui se comporte comme un ressort. Lorsque les deux extr mit s ont des temp ratures de une différence de température dans le conducteur ($\Delta T_0$), avec a température de la surface intérieure ($T_{is}$) et a température de la surface extérieure ($T_{es}$) :
La diff rence de temp rature implique que les atomes aux extr mit s oscillent de mani re diff rente ; les atomes dans la zone haute temp rature auront une amplitude plus grande dans leurs oscillations par rapport aux atomes dans la zone basse temp rature.
Cependant, cette diff rence conduira progressivement ce que toute la cha ne oscille de telle mani re qu' la fin, l'amplitude variera le long du chemin, depuis les valeurs les plus lev es l o la temp rature est galement plus lev e, jusqu'aux valeurs les plus basses dans la zone basse temp rature.
De cette mani re, a différence de température dans le conducteur ($\Delta T_0$) m ne une chaleur transportée ($dQ$) en une variation temporelle ($dt$).
L'un des facteurs cl s d terminant la quantit de chaleur pouvant tre conduite travers un solide ou un liquide est sa section transversale, c'est- -dire la quantit de cha nes d'atomes disponibles. Plus nous avons de ces cha nes, plus notre capacit de transport de chaleur est grande.
Cependant, la longueur de ces cha nes peut tre contreproductive. mesure que la cha ne de ressorts devient plus longue, notre capacit transmettre la chaleur diminue, car de plus en plus d'atomes doivent ajuster leurs amplitudes d'oscillation.
Si nous repr sentons cela avec a section ($S$) et le longueur du pilote ($L$), le diagramme prend la forme suivante :
Enfin, la capacit du milieu et du mat riau transporter la chaleur, d crite par les coefficients le coefficient de transmission interne ($\alpha_i$) et le coefficient de transmission externe ($\alpha_e$), ainsi que a conductivité thermique ($\lambda$), explique comment la chaleur se d place en r ponse a différence de température ($\Delta T$) cr e par la diff rence entre a température intérieure ($T_i$) et a température extérieure ($T_e$) :
Ceci est calcul comme suit :
La conduction thermique a t mod lis e pour la premi re fois par Jean Baptiste Joseph Fourier [1], qui a tabli que a débit de chaleur ($q$), d fini par a chaleur transportée ($dQ$), a variation temporelle ($dt$) et a section ($S$), est exprim e par :
Cette th orie est galement li e a section ($S$), le longueur du pilote ($L$), a différence de température dans le conducteur ($\Delta T_0$) et a conductivité thermique ($\lambda$), comme illustr dans :
et est d crite avec le diagramme suivant :
[1] "Th orie Analytique de la Chaleur", Jean Baptiste Joseph Fourier, 1822.
Le principal moteur du transfert de chaleur d'un milieu un conducteur est la diff rence de temp rature. Dans le milieu a température intérieure ($T_i$), les particules ont plus d' nergie, et lorsqu'elles entrent en collision avec celles du conducteur une température de la surface intérieure ($T_{is}$), elles ont tendance augmenter l' nergie de ce dernier. Cette interaction peut tre repr sent e comme suit :
Au-del de la temp rature en elle-m me, le flux de chaleur d pend de a différence de température à l'interface interne ($\Delta T_i$) :
Un autre facteur cl est le nombre d'atomes dont l'amplitude d'oscillation peut tre augment e, ce qui d pend de a section ($S$). Enfin, nous devons galement prendre en compte les propri t s de surface, d crites par le coefficient de transmission interne ($\alpha_i$), qui correspondent la relation entre la chaleur transmise, la surface, la diff rence de temp rature et le temps coul :
De cette mani re, nous tablissons une relation qui nous permet de calculer a débit de chaleur ($q$) en fonction de a différence de température à l'interface interne ($\Delta T_i$) et le coefficient de transmission interne ($\alpha_i$) :
Cela peut s'exprimer math matiquement comme suit :
Le principal moteur du transfert de chaleur d'un conducteur un milieu est la diff rence de temp rature. Lorsque a température de la surface extérieure ($T_{es}$), les particules ont plus d' nergie et oscillent avec une amplitude plus grande en interagissant avec les atomes et les mol cules du milieu une température extérieure ($T_e$). Cela a tendance augmenter l' nergie de ces derniers. Cette interaction peut tre repr sent e comme suit :
Au-del de la temp rature, le flux de chaleur d pend de a différence de température à l'interface externe ($\Delta T_e$).
Un autre facteur cl est le nombre d'atomes qui peuvent avoir leur amplitude d'oscillation augment e, ce qui d pend de a section ($S$). Enfin, nous devons galement tenir compte des propri t s de surface, repr sent es par le coefficient de transmission externe ($\alpha_e$), qui correspondent la relation entre la chaleur transf r e, la surface, la diff rence de temp rature et le temps coul :
De cette mani re, nous tablissons une relation qui nous permet de calculer a débit de chaleur ($q$) en fonction de a différence de température à l'interface externe ($\Delta T_e$) et le coefficient de transmission externe ($\alpha_e$) :
Cela peut tre exprim math matiquement comme suit :
Les mod les de transfert de chaleur et de conduction sugg rent qu'il est possible de d velopper une relation qui int gre ces trois m canismes ensemble. Cette quation devrait prendre en compte a chaleur transportée ($dQ$), a variation temporelle ($dt$), a différence de température ($\Delta T$), a section ($S$) et le coefficient de transport total (supports multiples, deux interfaces) ($k$) :
Math matiquement, cela peut s'exprimer comme suit :
L'un des effets du transfert de chaleur d'un conducteur un milieu externe est le r chauffement du milieu pr s de l'interface, cr ant une zone d'interf rence dans la transmission. Cela diminue l'efficacit du transfert et tend former une couche isolante qui r duit le flux d' nergie.
Cependant, cet effet peut changer en pr sence de vent. Le vent peut liminer la couche d'atomes et de mol cules haute temp rature, am liorant ainsi l'efficacit du transfert de chaleur. Cela sugg re que le coefficient de transmission ($\alpha$) est influenc par a vitesse moyenne ($v_m$) [1,2] :
Dans ce contexte, nous mod lisons la relation en fonction de ERROR:9844,0 et d'un facteur de r f rence de le vitesse de référence du support ($v_0$).
La relation math matique qui d crit ce ph nom ne pour un gaz avec le coefficient de transmission dans les gaz, en fonction de la vitesse ($\alpha_{gv}$), a vitesse moyenne ($v_m$), le coefficient de transmission dans les gaz, indépendant de la vitesse ($\alpha_{g0}$) et le coefficient de transmission Facteur de vitesse du gaz ($v_{g0}$) est :
Et pour un liquide avec le coefficient de transmission dans le liquide, en fonction de la vitesse ($\alpha_{wv}$), a vitesse moyenne ($v_m$), le coefficient de transmission dans le liquide, indépendant de la vitesse ($\alpha_{w0}$) et le coefficient de transmission Facteur de vitesse du liquide ($v_{w0}$) :
Cela illustre comment le vent peut influencer de mani re significative l'efficacit du transfert de chaleur entre un conducteur et un milieu externe.
[1] " ber Fl ssigkeitsbewegung bei sehr kleiner Reibung" (Sur le mouvement des fluides avec tr s peu de friction), Ludwig Prandtl, 1904
[2] "Die Abh ngigkeit der W rme bergangszahl von der Rohrl nge" (La d pendance du coefficient de transfert de chaleur la longueur du tuyau), Wilhelm Nusselt, 1910
Dans le cas d'un solide, et de mani re similaire pour un liquide, nous pouvons d crire le syst me comme une structure d'atomes li s par quelque chose qui se comporte comme un ressort. Lorsque les deux extr mit s ont des temp ratures de une différence de température dans le conducteur ($\Delta T_0$), avec a température de la surface intérieure ($T_{is}$) et a température de la surface extérieure ($T_{es}$) :
A différence de température ($\Delta T$) est calcul en soustrayant a température extérieure ($T_e$) et a température intérieure ($T_i$), ce qui s'exprime comme suit :
Le flux de chaleur ($q$) est une fonction de a conductivité thermique ($\lambda$), le longueur du pilote ($L$) et a différence de température dans le conducteur ($\Delta T_0$)xa0:
A différence de température à l'interface interne ($\Delta T_i$) est calcul en soustrayant a température de la surface intérieure ($T_{is}$) de a température intérieure ($T_i$) :
De cette mani re, nous tablissons une relation qui nous permet de calculer a débit de chaleur ($q$) en fonction de a différence de température à l'interface interne ($\Delta T_i$) et le coefficient de transmission interne ($\alpha_i$) :
A différence de température à l'interface externe ($\Delta T_e$) est calcul en soustrayant a température de la surface extérieure ($T_{es}$) de a température extérieure ($T_e$) :
De cette mani re, nous tablissons une relation qui nous permet de calculer a débit de chaleur ($q$) en fonction de a différence de température à l'interface externe ($\Delta T_e$) et le coefficient de transmission externe ($\alpha_e$) :
De cette mani re, nous tablissons une relation qui nous permet de calculer a débit de chaleur ($q$) en fonction de le coefficient de transport total (supports multiples, deux interfaces) ($k$) et a différence de température ($\Delta T$) :
Dans le processus de transfert de chaleur, la temp rature diminue progressivement du syst me ayant la plus haute temp rature (interne) vers celui ayant la plus basse temp rature (externe). Dans ce processus, elle diminue d'abord de la temp rature moyenne interne a différence de température à l'interface interne ($\Delta T_i$), puis a différence de température dans le conducteur ($\Delta T_0$), et enfin a différence de température à l'interface externe ($\Delta T_e$). La somme de ces trois variations quivaut la chute totale, c'est- -dire a différence de température ($\Delta T$), comme illustr ci-dessous :
La valeur de le coefficient de transport total ($k$) dans l' quation de transport est d termin e en utilisant le coefficient de transmission externe ($\alpha_e$), le coefficient de transmission interne ($\alpha_i$), a conductivité thermique ($\lambda$) et le longueur du pilote ($L$) comme suit :
A température de la surface intérieure ($T_{is}$) n'est pas gal la temp rature du milieu lui-m me, qui est a température intérieure ($T_i$). Cette temp rature peut tre calcul e partir de a différence de température ($\Delta T$), le coefficient de transport total (supports multiples, deux interfaces) ($k$) et le coefficient de transmission interne ($\alpha_i$) en utilisant la formule suivante :
A température de la surface extérieure ($T_{es}$) n'est pas gal la temp rature du milieu, qui est a température extérieure ($T_e$). Cette temp rature peut tre calcul e partir de a différence de température ($\Delta T$), le coefficient de transport total (supports multiples, deux interfaces) ($k$), et le coefficient de transmission externe ($\alpha_e$) en utilisant la formule suivante :
La valeur de le coefficient de transport total ($k$) dans l' quation de transport est d termin e l'aide de le coefficient de transmission externe ($\alpha_e$), a conductivité thermique ($\lambda$) et le longueur du pilote ($L$) comme suitxa0:
La valeur de a débit de chaleur ($q$) dans l' quation de transport est d termin e l'aide de le coefficient de transmission interne ($\alpha_i$), le coefficient de transmission externe ($\alpha_e$), a élément de conductivité thermique i ($\lambda_i$) et ERROR:9880 < /var> comme suitxa0:
Dans le cas o un milieu se d place avec une constante de ERROR:5250.1 et que le coefficient de transmission dans les gaz, en fonction de la vitesse ($\alpha_{gv}$) est gal
o le coefficient de transmission dans les gaz, indépendant de la vitesse ($\alpha_{g0}$) repr sente le sc nario o le milieu ne se d place pas, et le coefficient de transmission Facteur de vitesse du gaz ($v_{g0}$) est la vitesse de r f rence.
La constante de transfert thermique pour le mat riau dans le cas d'un gaz au repos est de $5.6 J/m^2sK$, tandis que la vitesse de r f rence est de $1.41 m/s$.
Si un milieu se d place avec une constante de le coefficient de transmission dans le liquide, en fonction de la vitesse ($\alpha_{wv}$), et que a vitesse moyenne ($v_m$) est gal
o le coefficient de transmission dans le liquide, indépendant de la vitesse ($\alpha_{w0}$) repr sente le cas o le milieu ne se d place pas, et le coefficient de transmission Facteur de vitesse du liquide ($v_{w0}$) est la vitesse de r f rence.
La constante de transfert thermique du mat riau pour le cas d'un liquide au repos est gale $340 J/m^2sK$, tandis que la vitesse de r f rence est de $0,0278 m/s$.
La mod lisation de la conductivit thermique dans un milieu poreux tel que le sol est un d fi. Dans cette tude, des analyses ont t effectu es sur un large chantillon de pr l vements, et un mod le num rique a t d velopp pour pr dire a conductivité thermique dans un sol sec ($\lambda_b$) en fonction des textures du sol [1].
La relation de a conductivité thermique dans un sol sec ($\lambda_b$) a t d termin e en fonction de a conductivité thermique dans le sable ($\lambda_a$), a conductivité thermique dans le limon ($\lambda_i$), a conductivité thermique dans l'argile ($\lambda_c$) et a fraction massique de sable dans l'échantillon ($g_a$), a fraction massique de limon dans l'échantillon ($g_i$), a fraction massique d'argile dans l'échantillon ($g_c$), en utilisant la formule suivante :
[1] "Physical principles and calculation methods of moisture and heat transfer in cable trenches." (Principes physiques et m thodes de calcul de transfert d'humidit et de chaleur dans les tranch es de c bles), Brakelmann, H., etz-Report 19, 93 p. (1984), Berlin; Offenbach.
La mod lisation de la conductivit thermique dans un milieu poreux tel que le sol est un d fi. Dans cette tude, des analyses ont t effectu es sur un large chantillon de pr l vements, et un mod le num rique a t d velopp pour pr dire a conductivité thermique dans un sol sec ($\lambda_b$) en fonction des textures du sol [1].
La relation de a conductivité thermique dans un sol sec ($\lambda_b$) a t d termin e en fonction de a conductivité thermique dans le sable ($\lambda_a$), a conductivité thermique dans le limon ($\lambda_i$), a conductivité thermique dans l'argile ($\lambda_c$) et a fraction massique de sable dans l'échantillon ($g_a$), a fraction massique de limon dans l'échantillon ($g_i$), a fraction massique d'argile dans l'échantillon ($g_c$), en utilisant la formule suivante :
[1] "Physical principles and calculation methods of moisture and heat transfer in cable trenches." (Principes physiques et m thodes de calcul de transfert d'humidit et de chaleur dans les tranch es de c bles), Brakelmann, H., etz-Report 19, 93 p. (1984), Berlin; Offenbach.
ID:(2054, 0)