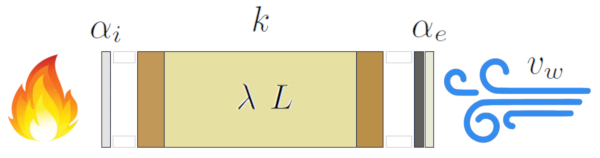Utilizador:
Transporte de calor
Storyboard 
A umidade do solo depende da sua temperatura, tornando importante calcular essa distribuição. Essa relação é determinada pelo fluxo de calor que é trocado com a superfície do solo.
ID:(2054, 0)
Transporte de calor
Storyboard
A umidade do solo depende da sua temperatura, tornando importante calcular essa distribuição. Essa relação é determinada pelo fluxo de calor que é trocado com a superfície do solo.
Variáveis
Cálculos
para 
,
depois, selecione a variável: 
para 
Cálculos
Variáve
Dado
Calcular
Objetivo :
Equação
A ser usado
Equações
Com la diferença de temperatura na interface interna ($\Delta T_i$), la diferença de temperatura no condutor ($\Delta T_0$), la diferença de temperatura na interface externa ($\Delta T_e$) e la diferença de temperatura ($\Delta T$), obtemos
que pode ser reescrito com la calor transportado ($dQ$), la variação de tempo ($dt$), la seção ($S$)
e com la condutividade térmica ($\lambda$) e o comprimento do conductor ($L$)
como
$\Delta T_i + \Delta T_0 + \Delta T_e = \displaystyle\frac{1}{S} \displaystyle\frac{dQ}{dt} \left(\displaystyle\frac{1}{\alpha_i} + \displaystyle\frac{1}{\alpha_e} + \displaystyle\frac{L}{\lambda}\right)$
ent o podemos definir um coeficiente combinado como
Com la diferença de temperatura na interface interna ($\Delta T_i$), la diferença de temperatura no condutor ($\Delta T_0$), la diferença de temperatura na interface externa ($\Delta T_e$) e la diferença de temperatura ($\Delta T$), obtemos
que pode ser reescrito com la calor transportado ($dQ$), la variação de tempo ($dt$), la seção ($S$)
e com la condutividade térmica ($\lambda$) e o comprimento do conductor ($L$)
e
como
$\Delta T = \Delta T_i + \Delta T_0 + \Delta T_e = \displaystyle\frac{1}{S} \frac{dQ}{dt} \left(\displaystyle\frac{1}{\alpha_i} + \displaystyle\frac{1}{\alpha_e} + \displaystyle\frac{L}{\lambda}\right) = \displaystyle\frac{1}{Sk} \displaystyle\frac{dQ}{dt}$
resultando em
Com la calor transportado ($dQ$), la variação de tempo ($dt$), la seção ($S$), la diferença de temperatura ($\Delta T$) e o coeficiente de transporte total (médio múltiplo, duas interfaces) ($k$), temos
o que, com o coeficiente de transmissão interna ($\alpha_i$) e la diferença de temperatura na interface interna ($\Delta T_i$)
resulta em
$k\Delta T = \alpha_i \Delta T_i$
e com la temperatura interna ($T_i$) e la temperatura da superfície interna ($T_{is}$) e
resulta em
Com la calor transportado ($dQ$), la variação de tempo ($dt$), la seção ($S$), la diferença de temperatura ($\Delta T$) e o coeficiente de transporte total (médio múltiplo, duas interfaces) ($k$), obtemos
que, com o coeficiente de transmissão externa ($\alpha_e$) e la diferença de temperatura na interface externa ($\Delta T_e$)
resulta em
$k\Delta T = \alpha_e \Delta T_e$
e com la temperatura externa ($T_e$) e la temperatura da superfície externa ($T_{es}$) e
resulta em
Exemplos
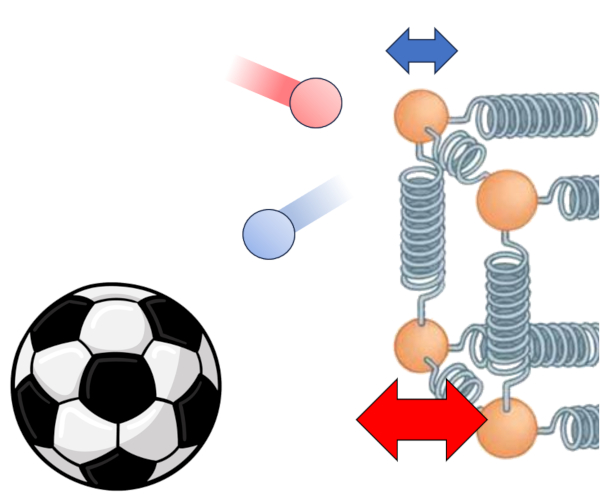
No caso de um s lido e de maneira semelhante para um l quido, podemos descrever o sistema como uma estrutura de tomos ligados por algo que se comporta como uma mola. Quando ambas as extremidades t m temperaturas de uma diferença de temperatura no condutor ($\Delta T_0$), com la temperatura da superfície interna ($T_{is}$) e la temperatura da superfície externa ($T_{es}$):
A diferen a de temperatura implica que os tomos nas extremidades oscilam de forma diferente; os tomos na zona de alta temperatura ter o uma amplitude maior em suas oscila es em compara o com os tomos na zona de baixa temperatura.
No entanto, essa diferen a gradualmente levar toda a cadeia a oscilar de tal forma que, no final, a amplitude variar ao longo do caminho, desde os valores mais altos onde a temperatura tamb m maior, at os valores mais baixos na zona de menor temperatura.
Dessa forma, la diferença de temperatura no condutor ($\Delta T_0$) leva a uma calor transportado ($dQ$) em uma variação de tempo ($dt$).
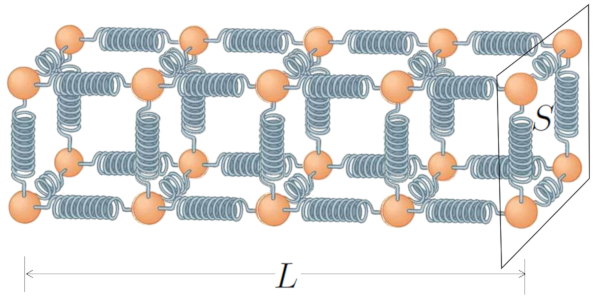
Um dos fatores-chave que determina quanto calor pode ser conduzido atrav s de um s lido ou l quido a sua se o transversal, ou seja, a quantidade de cadeias de tomos dispon veis. Quanto mais dessas cadeias tivermos, maior ser nossa capacidade de transporte de calor.
No entanto, o comprimento dessas cadeias pode ser contraproducente. medida que a cadeia de molas se torna mais longa, nossa capacidade de transmitir calor diminui, uma vez que mais tomos precisam ajustar suas amplitudes de oscila o.
Se representarmos isso com la seção ($S$) e o comprimento do conductor ($L$), o diagrama assume a seguinte forma:
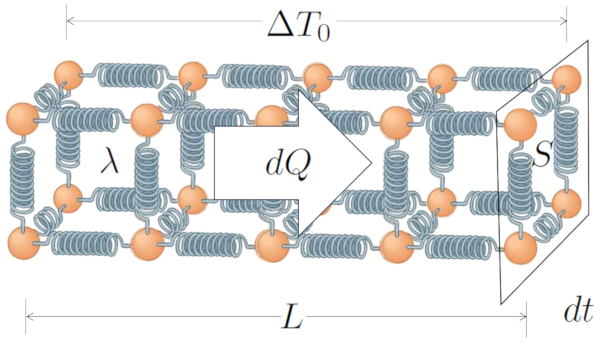
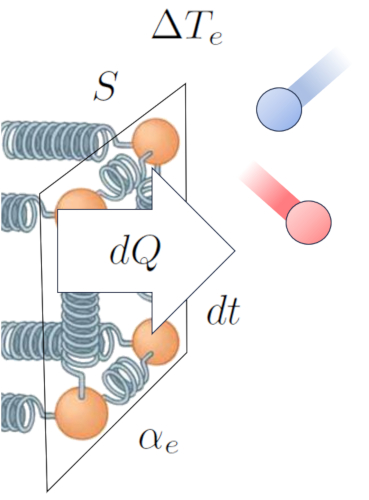
Por fim, a capacidade do meio e do material de transportar calor, descrita pelos coeficientes o coeficiente de transmissão interna ($\alpha_i$) e o coeficiente de transmissão externa ($\alpha_e$), e la condutividade térmica ($\lambda$), explica como o calor se desloca em resposta a la diferença de temperatura ($\Delta T$) criado pela diferen a entre la temperatura interna ($T_i$) e la temperatura externa ($T_e$):
Isso calculado da seguinte forma:
A condu o de calor foi modelada pela primeira vez por Jean Baptiste Joseph Fourier [1], que estabeleceu que la taxa de fluxo de calor ($q$), definido por la calor transportado ($dQ$), la variação de tempo ($dt$) e la seção ($S$), expressa pela:
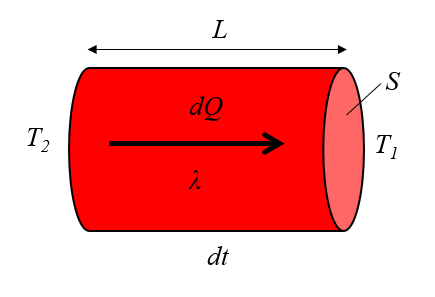
Esta teoria tamb m est relacionada a la seção ($S$), o comprimento do conductor ($L$), la diferença de temperatura no condutor ($\Delta T_0$) e la condutividade térmica ($\lambda$), conforme mostrado em:
e ilustrada pelo seguinte diagrama:
[1] "Th orie Analytique de la Chaleur" (A Teoria Anal tica do Calor), Jean Baptiste Joseph Fourier, 1822.
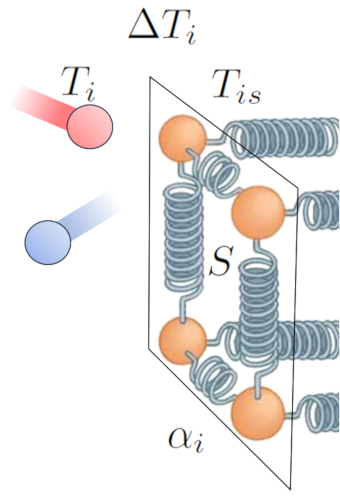
O principal impulsionador da transfer ncia de calor de um meio para um condutor a diferen a de temperatura. No meio la temperatura interna ($T_i$), as part culas t m mais energia e, ao colidirem com as do condutor a uma temperatura da superfície interna ($T_{is}$), tendem a aumentar a energia deste ltimo. Essa intera o pode ser representada da seguinte forma:
Al m da temperatura em si, o fluxo de calor depende de la diferença de temperatura na interface interna ($\Delta T_i$):
Outro fator fundamental o n mero de tomos aos quais a amplitude de oscila o pode ser aumentada, o que depende de la seção ($S$). Por fim, devemos considerar as propriedades da superf cie, descritas por o coeficiente de transmissão interna ($\alpha_i$), que corresponde rela o entre o calor transmitido, a rea superficial, a diferen a de temperatura e o tempo decorrido:
Dessa maneira, estabelecemos uma rela o que nos permite calcular la taxa de fluxo de calor ($q$) com base em la diferença de temperatura na interface interna ($\Delta T_i$) e o coeficiente de transmissão interna ($\alpha_i$):
Isso pode ser expresso matematicamente da seguinte forma:
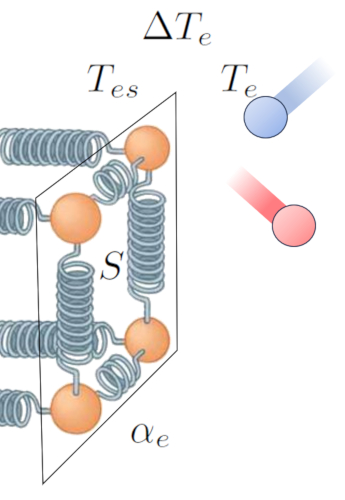
O principal impulsionador da transfer ncia de calor de um condutor para um meio a diferen a de temperatura. Quando la temperatura da superfície externa ($T_{es}$), as part culas t m mais energia e oscilam com uma amplitude maior ao interagirem com os tomos e mol culas do meio a uma temperatura externa ($T_e$). Isso tende a aumentar a energia destes ltimos. Essa intera o pode ser representada da seguinte forma:
Al m da temperatura, o fluxo de calor depende de la diferença de temperatura na interface externa ($\Delta T_e$).
Outro fator fundamental o n mero de tomos que podem ter aumentada a sua amplitude de oscila o, o que depende de la seção ($S$). Por fim, devemos considerar as propriedades superficiais, representadas por o coeficiente de transmissão externa ($\alpha_e$), que correspondem rela o entre o calor transmitido, a rea superficial, a diferen a de temperatura e o tempo decorrido:
Dessa forma, estabelecemos uma rela o que nos permite calcular la taxa de fluxo de calor ($q$) com base em la diferença de temperatura na interface externa ($\Delta T_e$) e o coeficiente de transmissão externa ($\alpha_e$):
Isso pode ser expresso matematicamente da seguinte maneira:
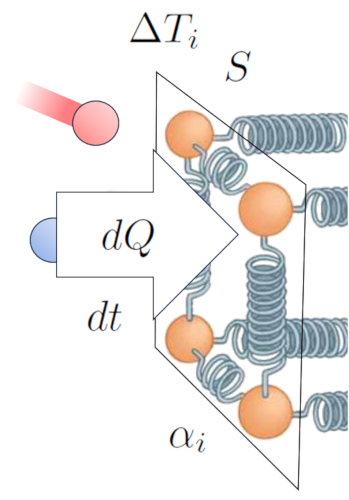
Os modelos de transfer ncia e condu o de calor sugerem que poss vel desenvolver uma rela o que incorpore os tr s mecanismos juntos. Esta equa o deve levar em considera o la calor transportado ($dQ$), la variação de tempo ($dt$), la diferença de temperatura ($\Delta T$), la seção ($S$) e o coeficiente de transporte total (médio múltiplo, duas interfaces) ($k$):
Matematicamente, isso pode ser expresso da seguinte forma:
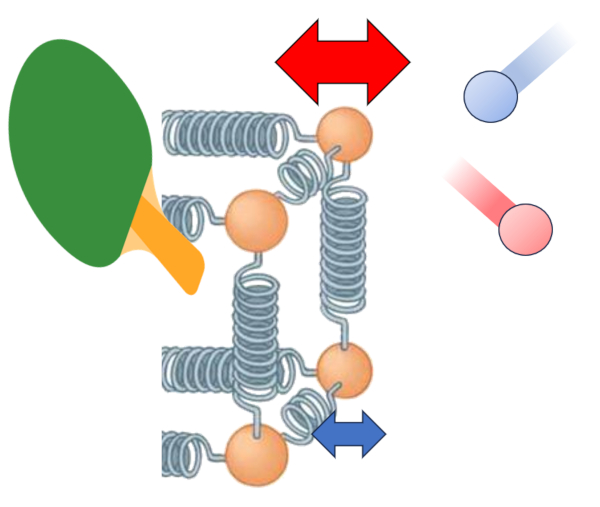
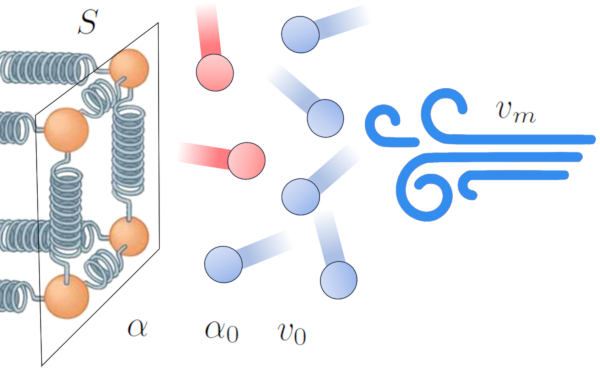
Um dos efeitos da transfer ncia de calor de um condutor para um meio externo o aquecimento do meio pr ximo interface, criando uma zona de interfer ncia na transmiss o. Isso diminui a efici ncia da transfer ncia e tende a formar uma camada isolante que reduz o fluxo de energia.
No entanto, esse efeito pode mudar na presen a de vento. O vento pode remover a camada de tomos e mol culas em alta temperatura, aumentando a efici ncia da transfer ncia de calor. Isso indica que o coeficiente de transmissão ($\alpha$) influenciado por la velocidade média ($v_m$) [1,2]:
Nesse contexto, modelamos a rela o com base em ERROR:9844,0 e um fator de refer ncia de o velocidade de referência de mídia ($v_0$).
A rela o matem tica que descreve esse fen meno para um g s com o coeficiente de transmissão em gases, dependente da velocidade ($\alpha_{gv}$), la velocidade média ($v_m$), o coeficiente de transmissão em gases, independente da velocidade ($\alpha_{g0}$) e o coeficiente de transmissão fator de velocidade do gás ($v_{g0}$) :
E para um l quido com o coeficiente de transmissão em líquido, dependente da velocidade ($\alpha_{wv}$), la velocidade média ($v_m$), o coeficiente de transmissão em líquido, independente da velocidade ($\alpha_{w0}$) e o coeficiente de transmissão fator de velocidade do líquido ($v_{w0}$):
Isso demonstra como o vento pode influenciar significativamente a efici ncia da transfer ncia de calor entre um condutor e um meio externo.
[1] " ber Fl ssigkeitsbewegung bei sehr kleiner Reibung" (Sobre o Movimento de Fluidos com Muito Pouca Fric o), Ludwig Prandtl, 1904
[2] "Die Abh ngigkeit der W rme bergangszahl von der Rohrl nge" (A Depend ncia do Coeficiente de Transfer ncia de Calor com o Comprimento da Tubula o), Wilhelm Nusselt, 1910
No caso de um s lido e de maneira semelhante para um l quido, podemos descrever o sistema como uma estrutura de tomos ligados por algo que se comporta como uma mola. Quando ambas as extremidades t m temperaturas de uma diferença de temperatura no condutor ($\Delta T_0$), com la temperatura da superfície interna ($T_{is}$) e la temperatura da superfície externa ($T_{es}$):
La diferença de temperatura ($\Delta T$) calculado subtraindo la temperatura externa ($T_e$) e la temperatura interna ($T_i$), o que expresso como:
O fluxo de calor ($q$) uma fun o de la condutividade térmica ($\lambda$), o comprimento do conductor ($L$) e la diferença de temperatura no condutor ($\Delta T_0$):
La diferença de temperatura na interface interna ($\Delta T_i$) calculado subtraindo la temperatura da superfície interna ($T_{is}$) de la temperatura interna ($T_i$):
Dessa maneira, estabelecemos uma rela o que nos permite calcular la taxa de fluxo de calor ($q$) com base em la diferença de temperatura na interface interna ($\Delta T_i$) e o coeficiente de transmissão interna ($\alpha_i$):
La diferença de temperatura na interface externa ($\Delta T_e$) calculado subtraindo la temperatura da superfície externa ($T_{es}$) de la temperatura externa ($T_e$):
Dessa forma, estabelecemos uma rela o que nos permite calcular la taxa de fluxo de calor ($q$) com base em la diferença de temperatura na interface externa ($\Delta T_e$) e o coeficiente de transmissão externa ($\alpha_e$):
Dessa forma, estabelecemos uma rela o que nos permite calcular la taxa de fluxo de calor ($q$) como fun o de o coeficiente de transporte total (médio múltiplo, duas interfaces) ($k$) e la diferença de temperatura ($\Delta T$):
No processo de transfer ncia de calor, a temperatura diminui gradualmente do sistema com a maior temperatura (interno) para o sistema com a menor temperatura (externo). Nesse processo, primeiro diminui da temperatura m dia interna para la diferença de temperatura na interface interna ($\Delta T_i$), depois para la diferença de temperatura no condutor ($\Delta T_0$) e finalmente para la diferença de temperatura na interface externa ($\Delta T_e$). A soma dessas tr s varia es equivale queda total, ou seja, la diferença de temperatura ($\Delta T$), como mostrado abaixo:
O valor de o coeficiente de transporte total ($k$) na equa o de transporte determinado usando o coeficiente de transmissão externa ($\alpha_e$), o coeficiente de transmissão interna ($\alpha_i$), la condutividade térmica ($\lambda$) e o comprimento do conductor ($L$) da seguinte forma:
La temperatura da superfície interna ($T_{is}$) n o igual temperatura do pr prio meio, que la temperatura interna ($T_i$). Essa temperatura pode ser calculada a partir de la diferença de temperatura ($\Delta T$), o coeficiente de transporte total (médio múltiplo, duas interfaces) ($k$) e o coeficiente de transmissão interna ($\alpha_i$) usando a seguinte f rmula:
La temperatura da superfície externa ($T_{es}$) n o igual temperatura do meio, que la temperatura externa ($T_e$). Essa temperatura pode ser calculada a partir de la diferença de temperatura ($\Delta T$), o coeficiente de transporte total (médio múltiplo, duas interfaces) ($k$) e o coeficiente de transmissão externa ($\alpha_e$) usando a seguinte f rmula:
O valor de o coeficiente de transporte total ($k$) na equa o de transporte determinado usando o coeficiente de transmissão externa ($\alpha_e$), la condutividade térmica ($\lambda$) e o comprimento do conductor ($L$) da seguinte forma:
O valor de la taxa de fluxo de calor ($q$) na equa o de transporte determinado usando o coeficiente de transmissão interna ($\alpha_i$), o coeficiente de transmissão externa ($\alpha_e$), la elemento de condutividade térmica i ($\lambda_i$) e ERROR:9880 < /var> da seguinte forma:
No caso de um meio se deslocar com uma constante de uma velocidade média ($v_m$) e o coeficiente de transmissão em gases, dependente da velocidade ($\alpha_{gv}$) ser igual a
onde o coeficiente de transmissão em gases, independente da velocidade ($\alpha_{g0}$) representa a situa o em que o meio n o se desloca e o coeficiente de transmissão fator de velocidade do gás ($v_{g0}$) a velocidade de refer ncia.
A constante de transfer ncia t rmica do material no caso de um g s em repouso igual a $5,6 J/m^2sK$, enquanto a velocidade de refer ncia de $1,41 m/s$.
Se um meio est se deslocando com uma constante de o coeficiente de transmissão em líquido, dependente da velocidade ($\alpha_{wv}$) e la velocidade média ($v_m$) igual a
onde o coeficiente de transmissão em líquido, independente da velocidade ($\alpha_{w0}$) representa o caso em que o meio n o est se deslocando, e o coeficiente de transmissão fator de velocidade do líquido ($v_{w0}$) a velocidade de refer ncia.
A constante de transfer ncia t rmica do material para o caso de um l quido em repouso igual a $340 J/m^2sK$, enquanto a velocidade de refer ncia de $0,0278 m/s$.
A modelagem da condutividade t rmica em um meio poroso, como o solo, um desafio. Neste estudo, foram realizadas an lises em uma ampla variedade de amostras e foi desenvolvido um modelo num rico para prever la condutividade térmica em solo seco ($\lambda_b$) com base nas texturas do solo [1].
A rela o de la condutividade térmica em solo seco ($\lambda_b$) foi determinada com base em la condutividade térmica na areia ($\lambda_a$), la condutividade térmica em lodo ($\lambda_i$), la condutividade térmica em argila ($\lambda_c$) e la fração mássica de areia na amostra ($g_a$), la fração de massa de lodo na amostra ($g_i$), la fração mássica de argila na amostra ($g_c$), usando a seguinte f rmula:
[1] "Physical principles and calculation methods of moisture and heat transfer in cable trenches." (Princ pios f sicos e m todos de c lculo de transfer ncia de umidade e calor em valas de cabos), Brakelmann, H., etz-Report 19, 93p. (1984), Berlim; Offenbach.
A modelagem da condutividade t rmica em um meio poroso, como o solo, um desafio. Neste estudo, foram realizadas an lises em uma ampla variedade de amostras e foi desenvolvido um modelo num rico para prever la condutividade térmica em solo seco ($\lambda_b$) com base nas texturas do solo [1].
A rela o de la condutividade térmica em solo seco ($\lambda_b$) foi determinada com base em la condutividade térmica na areia ($\lambda_a$), la condutividade térmica em lodo ($\lambda_i$), la condutividade térmica em argila ($\lambda_c$) e la fração mássica de areia na amostra ($g_a$), la fração de massa de lodo na amostra ($g_i$), la fração mássica de argila na amostra ($g_c$), usando a seguinte f rmula:
[1] "Physical principles and calculation methods of moisture and heat transfer in cable trenches." (Princ pios f sicos e m todos de c lculo de transfer ncia de umidade e calor em valas de cabos), Brakelmann, H., etz-Report 19, 93p. (1984), Berlim; Offenbach.
ID:(2054, 0)
