Aceleración angular constante
Storyboard
Para que un objeto alcance una velocidad angular determinada, primero debe aumentar su velocidad angular desde el reposo. Este proceso se denomina aceleración angular y se define en función de la variación de la velocidad angular en el tiempo. Por otro lado, si se busca reducir la velocidad angular e incluso detener la rotación del objeto, también se introduce una aceleración angular, pero con el signo opuesto al de la velocidad angular (si la velocidad angular es positiva, la aceleración angular es negativa, y viceversa), lo que se conoce como frenado angular.
ID:(612, 0)
Orientación: Aceleración angular media
Descripción
Con la variación de la velocidad angular y el tiempo transcurrido, podemos definir una aceleración angular media:

Esto nos permite predecir la velocidad angular futura siempre que la aceleración sea constante.
ID:(12519, 0)
Variación de velocidades angulares
Ecuación
La aceleración corresponde a la variación de la velocidad angular por unidad de tiempo.
Por lo tanto, la variación de la velocidad angular se expresa como:
ID:(3681, 0)
Aceleración angular media
Ecuación
La aceleración angular media se define como la proporción en la que varía la velocidad angular a lo largo del tiempo. Para medir esta magnitud, es necesario cuantificar cómo cambia la velocidad angular en el transcurso del tiempo.

La ecuación que describe esta aceleración angular media es la siguiente:
| $ \alpha \equiv \displaystyle\frac{ \Delta\omega }{ \Delta t }$ |
Es importante tener en cuenta que la aceleración angular media es una estimación de la aceleración angular real. Sin embargo, existe un problema fundamental:
Si la aceleración angular varía a lo largo del tiempo, el valor de la aceleración angular media puede diferir significativamente de la aceleración angular promedio.
Por lo tanto, la clave reside en
Determinar la aceleración angular en un intervalo de tiempo lo suficientemente corto para minimizar cualquier variación significativa.
ID:(3234, 0)
Aceleración y aceleración angular
Ecuación
Si dividimos la relación de la velocidad tangencial
| $ v = r \omega $ |
por el tiempo transcurrido, podemos obtener la razón que nos permite calcular la aceleración angular a lo largo de la órbita:
Dado que la aceleración de traslación es igual a
| $ a =\displaystyle\frac{ dv }{ dt }$ |
y la velocidad tangencial se expresa en función del radio y la velocidad angular
| $ v = r \omega $ |
y la aceleración angular media se define como
| $ \alpha \equiv \displaystyle\frac{ \Delta\omega }{ \Delta t }$ |
se deduce que
$a=\displaystyle\frac{\Delta v}{\Delta t}=r\displaystyle\frac{\Delta\omega}{\Delta t}=\alpha$
Dado que esta relación es general, se puede aplicar a los valores instantáneos, lo que lleva a
| $ a = r \alpha $ |
ID:(3236, 0)
Aceleración tangencial, forma vectorial
Ecuación
La aceleración angular se expresa como un vector en la dirección del eje de rotación. Dado que el radio de rotación y la aceleración angular son perpendiculares a la aceleración tangencial, se obtiene la siguiente relación:
| $ a = r \alpha $ |
Esta relación puede escribirse como el producto cruz entre la aceleración angular y el radio, representado de la siguiente manera:
Dado que la aceleración tangencial es
| $ a = r \alpha $ |
Si el versor del eje es $\hat{n}$ y el radial es $\hat{r}$, el versor tangencial puede calcularse mediante el producto cruz:
$\hat{t} = \hat{n} \times \hat{r}$
En consecuencia, considerando que
$\vec{a} = a \hat{t}$
,
$\vec{r} = r \hat{r}$
y
$\vec{\alpha} = \alpha \hat{n}$
,
podemos deducir que
$\vec{a} = a \hat{t} = a \hat{n} \times \hat{r} = r \alpha \hat{n} \times \hat{r} = \vec{\alpha} \times \vec{r}$
,
lo que se traduce en
| $ \vec{a} = \vec{\alpha} \times \vec{r} $ |
ID:(11598, 0)
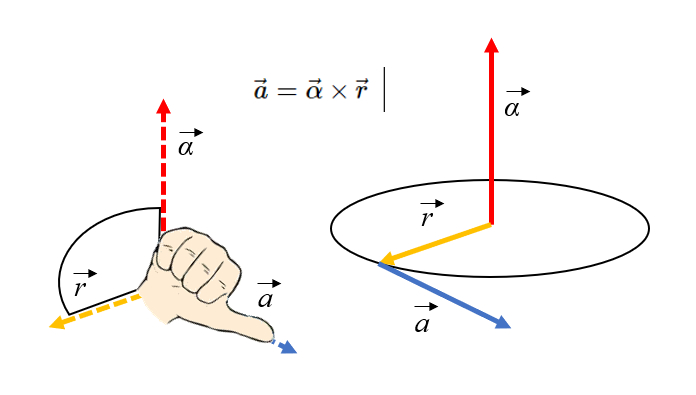
Aceleración tangencial, regla de la mano derecha
Imagen
La dirección de la aceleración tangencial puede determinarse utilizando la regla de la mano derecha, donde los dedos se orientan hacia el eje y luego se giran en dirección al radio:
ID:(11600, 0)
