Velocidad constante
Storyboard 
Para describir cómo evoluciona la posición en el tiempo, es necesario analizar la variación de ésta a lo largo del tiempo.
La relación entre la variación de la posición equivale a la distancia recorrida en el tiempo transcurrido, que, al dividirla por dicho tiempo, se convierte en la velocidad.
Cuando se considera un intervalo de tiempo finito, la velocidad representa la velocidad promedio durante ese lapso.
ID:(608, 0)
Posición
Imagen 
La posición ($s$) de un objeto en un sistema unidimensional se refiere a la ubicación del objeto en relación con un punto de referencia. Esta ubicación se expresa como la distancia entre el objeto y el punto de origen. Esta distancia puede ser una línea recta en un eje cartesiano, o puede seguir un camino curvo:
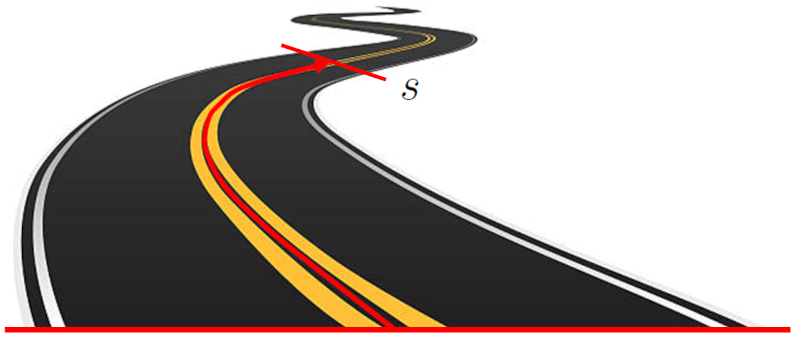
ID:(15, 0)
Posición inicial
Nota 
La posición inicial ($s_0$) es la ubicación inicial de un objeto antes de que comience un movimiento. Esta ubicación se define como la distancia entre el objeto y el punto de origen. Esta distancia puede ser una línea recta sobre un eje cartesiano, o puede seguir una trayectoria curva.
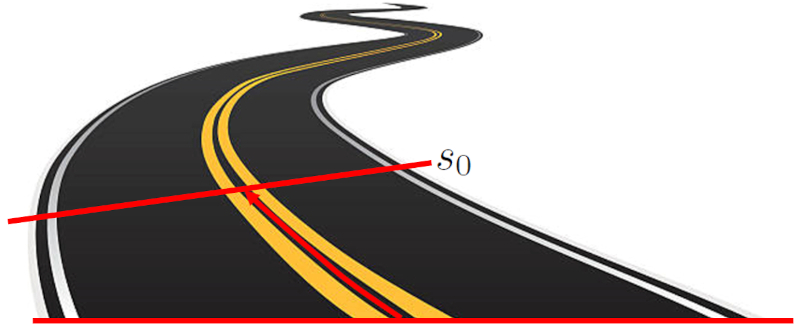
ID:(10302, 0)
Distancia recorrida
Cita 
La distancia recorrida en un tiempo ($\Delta s$) por un objeto se mide midiendo la distancia entre dos puntos específicos a lo largo de una trayectoria. Esta trayectoria puede ser una línea recta en un eje cartesiano, o bien un camino curvo. La distancia se calcula midiendo la longitud de la trayectoria entre los dos puntos de partida y llegada.
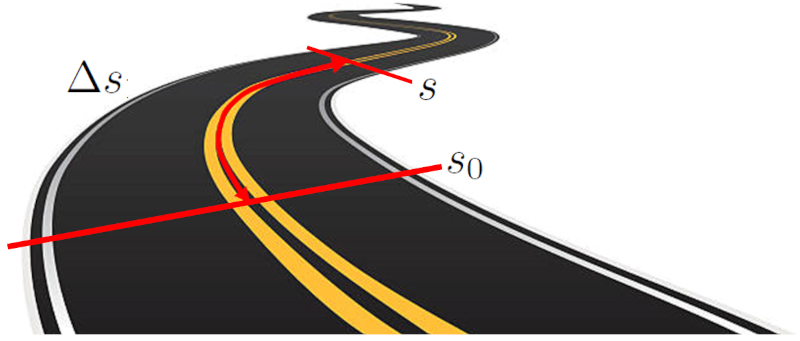
ID:(9495, 0)
Velocidad como pendiente de la curva posición
Audio 
Si se representa el desplazamiento como una recta entre el origen O y el punto A:
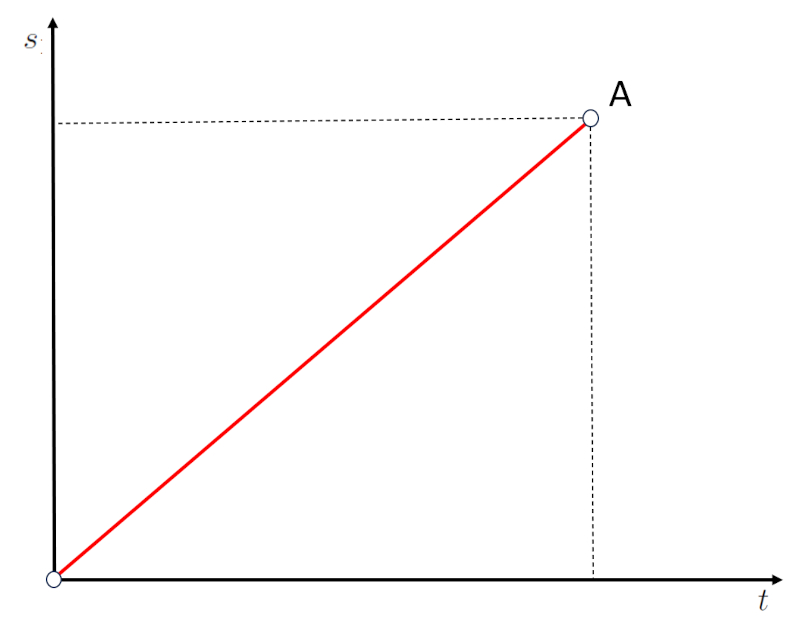
Diagrama posición-tiempo
se observa que se ha recorrido una distancia en un tiempo transcurrido. Por lo tanto, la pendiente de la gráfica distancia vs tiempo transcurrido corresponde a la velocidad.
Si la pendiente es mayor, significa que se ha recorrido una mayor distancia en un tiempo menor, lo que corresponde a una velocidad mayor.
Si la pendiente es menor, significa que se ha recorrido una menor distancia en un tiempo mayor, lo que corresponde a una velocidad menor.
ID:(2239, 0)
Diagrama camino tiempo con segmento horizontal
Video 
Un segundo tipo de caso son segmentos horizontales en el diagrama camino vs tiempo:
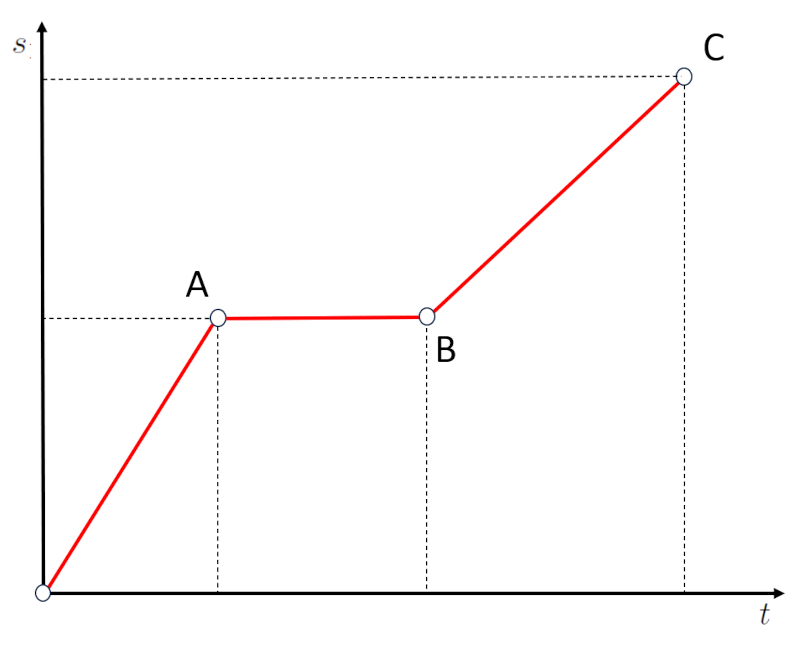
Si observamos el segmento AB notaremos que pese a que ha transcurrido tiempo el camino no ha variado. Esto significa que el objeto esta detenido. Por ello segmentos horizontales, que corresponden a una pendiente nula, corresponde a etapas en que la velocidad es nula.
ID:(2241, 0)
Gráfica camino tiempo para velocidad constante y tiempo inicial
Unidad 
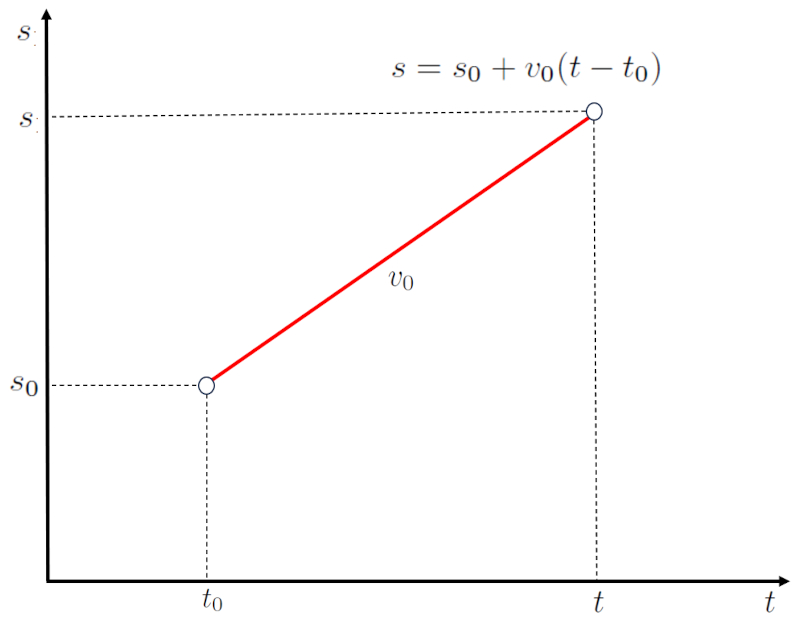
Para el caso de velocidad constante y tiempo inicial, la posición puede calcularse utilizando los valores la posición ($s$), la posición inicial ($s_0$), la velocidad constante ($v_0$), el tiempo ($t$) y el tiempo inicial ($t_0$) mediante la siguiente ecuación:
| $ s = s_0 + v_0 ( t - t_0 )$ |
que corresponde a una recta con:
• una pendiente igual a la velocidad constante ($v_0$)
• un punto de corte en la posición inicial ($s_0$) para el tiempo inicial ($t_0$)
que se muestra a continuación:
ID:(2243, 0)
Pendiente negativa
Code 
En el caso de la gráfica en la que un segmento tiene pendiente negativa:
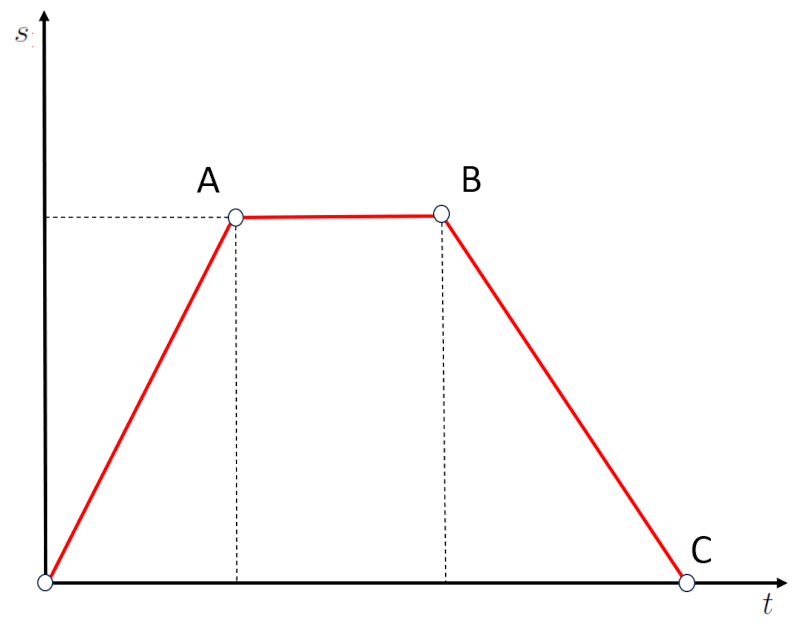
presenta una situación en la que se regresó de la posición B a C, la cual se encuentra a una distancia nula. En otras palabras, las pendientes negativas corresponden a viajar en dirección opuesta, no alejándose, sino acercándose al origen.
ID:(2245, 0)
Paradoja del cuerpo en reposo
Flujo 
Si un objeto se encuentra en "reposo", esto significa que está en reposo en relación a nuestro sistema de referencia o sistema de coordenadas. Sin embargo, este "reposo" es totalmente relativo. Es decir, desde el punto de vista de un objeto que se mueve con respecto a nuestro sistema, el objeto en "reposo" también está en movimiento.
En este sentido, no existe un "objeto en reposo" como algo absoluto, sino que es relativo a un sistema de referencia particular. Por lo tanto, en general, todas las mediciones de velocidad se realizan en relación a un sistema de referencia específico.
Por ejemplo, si un objeto parece desplazarse muy lentamente, esto solo significa que su velocidad es muy similar a la velocidad del sistema de referencia en el que se observa el movimiento lento.
ID:(4405, 0)
Velocidad constante
Descripción 
Para describir cómo evoluciona la posición en el tiempo, es necesario analizar la variación de ésta a lo largo del tiempo.
La relación entre la variación de la posición equivale a la distancia recorrida en el tiempo transcurrido, que, al dividirla por dicho tiempo, se convierte en la velocidad.
Variables
Cálculos
Cálculos
Ecuaciones
Con la distancia recorrida en un tiempo ($\Delta s$) es con la posición ($s$) y la posición inicial ($s_0$):
| $ \Delta s = s_2 - s_1 $ |
y el tiempo transcurrido ($\Delta t$) es con el tiempo ($t$) y el tiempo inicial ($t_0$):
| $ \Delta t \equiv t - t_0 $ |
Se tiene que la ecuaci n de la velocidad media:
| $ v_0 \equiv\displaystyle\frac{ \Delta s }{ \Delta t }$ |
puede escribirse como:
$v_0 = \bar{v} = \displaystyle\frac{\Delta s}{\Delta t} = \displaystyle\frac{s - s_0}{t - t_0}$
Por lo tanto, despejando, se obtiene:
| $ s = s_0 + v_0 ( t - t_0 )$ |
(ID 3154)
(ID 10276)
Ejemplos
(ID 2239)
(ID 2241)
(ID 2243)
(ID 2245)
(ID 4405)
ID:(608, 0)
