Constant angular acceleration
Storyboard
To achieve a certain angular velocity, an object must first increase its angular velocity from rest. This process is called angular acceleration and is defined in terms of the change in angular velocity over time. On the other hand, if the goal is to decrease the angular velocity and even stop the rotation of the object, angular deceleration is introduced, with the opposite sign to that of the angular velocity (if the angular velocity is positive, the angular deceleration is negative, and vice versa), known as angular braking.
ID:(612, 0)
Orientation: Mean Angular Acceleration
Description
With the variation of angular velocity and elapsed time, we can define an average angular acceleration:

This allows us to predict the future angular velocity as long as the acceleration remains constant.
ID:(12519, 0)
Variation of angular speeds
Equation
Acceleration corresponds to the change in angular velocity per unit of time.
Therefore, the change in angular velocity can be expressed as:
ID:(3681, 0)
Mean Angular Acceleration
Equation
The average angular acceleration is defined as the proportion in which the angular velocity changes over time. To measure this quantity accurately, it is necessary to quantify how the angular velocity changes over the course of time.

The equation that describes this average angular acceleration is as follows:
| $ \alpha \equiv \displaystyle\frac{ \Delta\omega }{ \Delta t }$ |
It is important to note that the average angular acceleration is an estimation of the actual angular acceleration. However, there is a fundamental issue:
If the angular acceleration varies over time, the value of the average angular acceleration can differ significantly from the average angular acceleration.
Therefore, the key lies in
Determining the angular acceleration within a sufficiently short time interval to minimize any significant variation.
ID:(3234, 0)
Acceleration and Angular Acceleration
Equation
To calculate the angular acceleration along the orbit, one can derive it by dividing the tangential velocity relationship
| $ v = r \omega $ |
by the elapsed time:
Since the translational acceleration is equal to
| $ a =\displaystyle\frac{ dv }{ dt }$ |
and the tangential velocity is expressed in terms of radius and angular velocity
| $ v = r \omega $ |
and the definition of average angular acceleration is
| $ \alpha \equiv \displaystyle\frac{ \Delta\omega }{ \Delta t }$ |
we have
$a=\displaystyle\frac{\Delta v}{\Delta t}=r\displaystyle\frac{\Delta\omega}{\Delta t}=\alpha$
Since this relation is general, it can be applied to instantaneous values, resulting in
| $ a = r \alpha $ |
ID:(3236, 0)
Tangential acceleration, vector shape
Equation
Angular acceleration is represented as a vector aligned with the axis of rotation. Because the radius of rotation and angular acceleration are orthogonal to tangential acceleration, we have:
| $ a = r \alpha $ |
This relationship can be expressed as the cross product of angular acceleration and radius, written as:
Given that the tangential acceleration is
| $ a = r \alpha $ |
If the unit vector of the axis is $\hat{n}$ and the radial unit vector is $\hat{r}$, the tangential unit vector can be calculated using the cross product:
$\hat{t} = \hat{n} \times \hat{r}$
As a result, considering that
$\vec{a} = a \hat{t}$
,
$\vec{r} = r \hat{r}$
, and
$\vec{\alpha} = \alpha \hat{n}$
,
we can deduce that
$\vec{a} = a \hat{t} = a \hat{n} \times \hat{r} = r \alpha \hat{n} \times \hat{r} = \vec{\alpha} \times \vec{r}$
,
which translates to
| $ \vec{a} = \vec{\alpha} \times \vec{r} $ |
.
ID:(11598, 0)
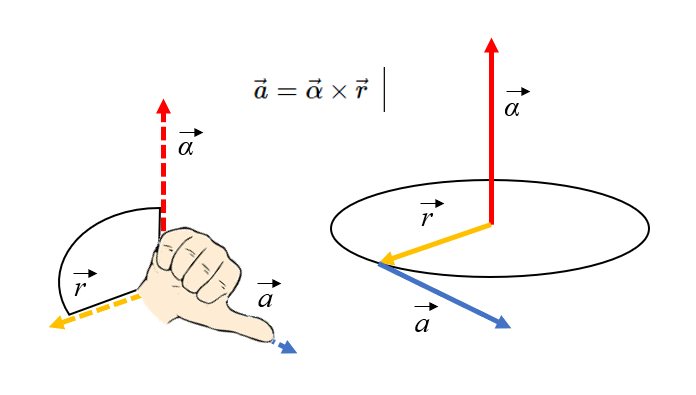
Tangential acceleration, right hand rule
Image
The orientation of tangential acceleration can be obtained using the right-hand rule, with fingers pointing towards the axis and then rotating towards the radius:
ID:(11600, 0)
