Storyboard

Any object with velocity tends to move in a straight line. To follow a circular orbit, an object needs to "fall" radically from its straight path to the orbit's radius. This "fall" corresponds to centripetal acceleration (centri = center, petal = toward), as observed by an external observer.

On the other hand, if the object continues on its straight path instead of following the circular orbit, an observer within the rotating system would perceive the same acceleration, but moving away from the center. This is known as centrifugal acceleration (centri = center, fuga = moving away).

>Model

ID:(758, 0)

Description

>Top

If an object is subjected to a mode of maintaining a constant radius, it will rotate as indicated in the figure. Upon observing the figure, one would notice that the mass undergoes a translational motion with a tangential velocity that is equal to the radius times the angular velocity:

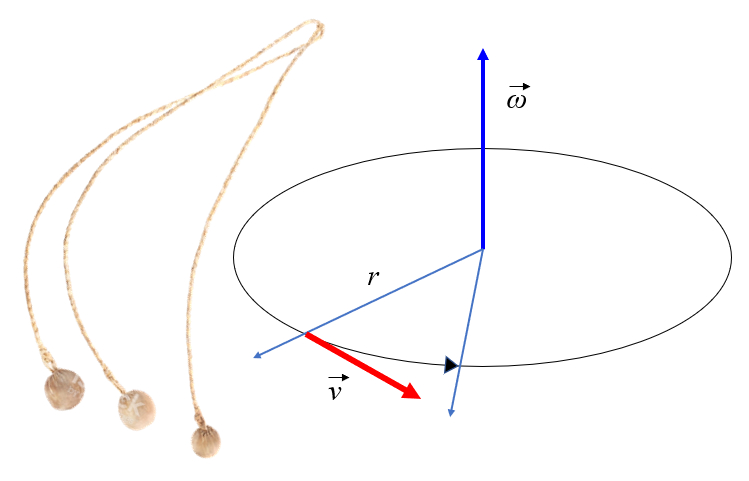
However, if the element connecting the object to the axis is cut, the object will continue to move tangentially in a straight line.

ID:(310, 0)

Description

>Top

If a body fixed to a rope of length $r$ rotates with a tangential velocity $v$, and the rope is cut, the body will continue to move in a straight line with a constant velocity $v$ due to inertia.

Orbit circulates of radio r and path traveled v\,dt in case the object is not retained. Both distances represent the legs of a hypotenuse rectangle of length equal to the radius r and the radial distance x traveled. Applying Pythagoras can thus estimate this path x as a function of time t.

In a time interval $\Delta t$, the body will have traveled a distance of $v\Delta t$ tangentially to its previous orbit. From the perspective of an observer on the axis of the rotating system, the distance is calculated using the Pythagorean theorem, by adding the square of the orbit radius to the square of the distance traveled:

$\sqrt{r^2+v^2\Delta t^2}$

ID:(1155, 0)

Description

>Top

If we study a catapult, we will notice that the projectile initially moves along the curve described by the spoon. This happens because the spoon is designed to hold the projectile. Once the arm stops, the projectile continues in a straight line tangential to the circle it was following.

If an object is not restrained and travels with a tangential velocity $v$, it will cover a distance of $v\Delta t$ in a time interval $\Delta t$, moving from point B to point C. However, if it continues to orbit, after the time interval $\Delta t$, it will reach point D. If the object reaches point C, from the perspective of an observer on Earth, there will be an acceleration that causes the object to move away from Earth (centrifugal acceleration), covering the distance $\Delta r$ in the time interval $\Delta t$.

For an observer in space, an object in orbit is constantly falling: instead of ending up at point C, it falls over the time interval $\Delta t$ covering the distance $\Delta r$ until it reaches point D. In both cases, we can represent the situation graphically, and using the Pythagorean theorem, we can see that the following equation must hold true:

$(r+\Delta r)^2=r^2+(v\Delta t)^2$

Expanding the equation, we get:

$2\Delta rr+\Delta r^2=v^2\Delta t^2$

Since the variation in radius $\Delta r$ is much smaller than the radius itself ($r\ll\Delta r$), we can conclude that:

$2\Delta rr=v^2\Delta t^2$

Solving for $\Delta r$, we find:

$\Delta r=\displaystyle\frac{1}{2}\displaystyle\frac{v^2}{r}\Delta t^2$

Comparing this equation with the equation $s=at^2/2$, we can conclude that the object is accelerating with an acceleration equal to $v^2/r$.

ID:(313, 0)

Equation

>Top, >Model

Bodies tend, by inertia, to move in a straight line at a constant velocity. Therefore, if a body orbits around another, it deviates from its straight path and 'falls' into an orbit. Similarly, if there is nothing to hold a body, it will start moving away from the orbit, experiencing, for an object at the center of the rotating system, an apparent acceleration that moves it away from the center, known as centrifugal acceleration. The acceleration is defined as:

$ a_c =\displaystyle\frac{ v ^2}{ r }$

Conditions

Variables

$a_c$

Centrifuge Acceleration

$m/s^2$

$r$

Radio

$m$

$v$

Speed

$m/s$

Relation

Development

If the distance traveled is small ($v\Delta t\ll r$), the square root of the distance between the center and the body,

$\sqrt{r^2+(v\Delta t)^2}$

can be approximated as

$r+\displaystyle\frac{1}{2}\displaystyle\frac{v^2}{r}\Delta t^2$

which corresponds to a parabolic relationship with respect to time $\Delta t$. Therefore, the behavior can be described with an acceleration equal to:

$ a_c =\displaystyle\frac{ v ^2}{ r }$

Centrifugal acceleration is an acceleration observed by a system on the axis of rotation when an object moves away (flees) at a constant velocity. For the object moving away, such acceleration does not exist.

ID:(4735, 0)

Equation

>Top, >Model

If we express the tangential velocity in terms of angular velocity, the centrifugal acceleration is given by:

$ a_c = r \omega ^2$

Conditions

Variables

$a_c$

Centrifuge Acceleration

$m/s^2$

$\omega$

Instantaneous Angular Speed

$rad/s$

$r$

Radio

$m$

Relation

Development

Since the centrifugal acceleration is equal to

$ a_c =\displaystyle\frac{ v ^2}{ r }$

with v as the velocity and r as the radius, and considering the relationship between tangential velocity and angular velocity as

$ v = r \omega $

we can conclude that:

$ a_c = r \omega ^2$

ID:(4384, 0)

Equation

>Top, >Model

When an object orbits at a radius $r$ with a tangential velocity $v$, it maintains a constant distance from the center equal to the radius.

For an observer external to the system, the body, which would otherwise travel in a straight line due to inertia, deviates from this trajectory while maintaining the distance from the center. From the perspective of this observer, the body is accelerating towards the center (centripetal acceleration) of the orbit. Unlike centrifugal acceleration, the object is experiencing a real acceleration. The magnitude of this acceleration is equal to the centrifugal acceleration but with the opposite sign. Therefore, the magnitude of the centripetal acceleration is:

Unlike centrifugal acceleration, the centripetal acceleration is measurable for the object that is literally 'falling\' towards the center.

ID:(4383, 0)