Druyd:Knowledge

Probabilidad de Complicaciones en Tejido Normal (NTCP)

Storyboard

>Modelo

ID:(741, 0)

Análisis de la fracción de tejido y su dosis

Definición

ID:(2714, 0)

Modelo de Lyman-Kutcher-Burman (NTCP)

Imagen

ID:(2715, 0)

Factor DVH

Nota

Para poder estimar que tan bueno es un plan cuando la información es 3D se puede proceder a sumar todos los voxeles que tienen la misma dosis y así generar un diagrama unidimensional:

ID:(1501, 0)

Calculo del DVH

Cita

ID:(2718, 0)

Probabilidad de complicaciones en tejido normal (NTCP)

Ejercicio

El segundo aspecto claves dentro del desarrollo del tratamiento optimo es minimizar la probabilidad de efectos adversos por el tratamiento, lo que en ingles se denomina el normal tissue complication probability, NTCP. Existen varios modelos que permiten estimar dicha probabilidad.

ID:(1499, 0)

Comparación TCP y NTCP

Ecuación

ID:(2713, 0)

Probabilidad de Complicaciones en Tejido Normal (NTCP)

Descripción

Variables

Símbolo

Texto

Variable

Valor

Unidades

Calcule

Valor MKS

Unidades MKS

$D_1$

D_1

Dosis 1

$D_2$

D_2

Dosis 2

$D_3$

D_3

Dosis 3

$D_4$

D_4

Dosis 4

$D_5$

D_5

Dosis 5

$TD_{50}$

TD_50

Dosis Critica $50%$

$D_{eff}$

D_eff

Dosis Efectiva del Modelo LKB

$m$

Factor $m$ Pendiente de la Curva del Modelo LKB

$n$

Factor $n$ del Exponente del Modelo LKB

$t$

Factor $t$ de la Distribución del Modelo LKB

$v_1$

v_1

Factor de Volumen de Voxels de Dosis 1

$v_2$

v_2

Factor de Volumen de Voxels de Dosis 2

m^3

$v_3$

v_3

Factor de Volumen de Voxels de Dosis 3

$v_4$

v_4

Factor de Volumen de Voxels de Dosis 4

$v_5$

v_5

Factor de Volumen de Voxels de Dosis 5

$v_i$

v_i

Fracción de Volumen (Voxels)

$NTCP$

NTCP

Probabilidad de complicaciones en tejido sano (NTCP)

$NTCP_1$

NTCP_1

Probabilidad de complicaciones en tejido sano (NTCP), órgano 1

$NTCP_2$

NTCP_2

Probabilidad de complicaciones en tejido sano (NTCP), órgano 2

$V_i$

V_i

Volumen de Voxels $i$

m^3

$V$

Volumen Total Irradiado

m^3

Cálculos

Ecuación

Número

Primero, seleccione la ecuación:

, luego, seleccione la variable:

Símbolo

Ecuación

Resuelto

Traducido

Cálculos

Símbolo

Ecuación

Resuelto

Traducido

Variable

Dado

Calcule

Objetivo :

Ecuación

A utilizar

Ecuaciones

$NTCP=\displaystyle\frac{1}{\sqrt{2\pi}}\int_{-\infty}^t e^{-u^2/2}du$

NTCP=\displaystyle\frac{1}{\sqrt{2\pi}}\int_{-\infty}^t e^{-u^2/2}du

(ID 4699)

$NTCP=\displaystyle\frac{1}{1+e^{-1.5976t-0.07056t^3}}$

NTCP=1/(1+e^(-1.5976t-0.07056t^3))

(ID 4700)

$D_{eff}=\left(\sum_iv_iD_i^{1/n}\right)^n$

D_{eff}=\left(\sum_iv_iD_i^{1/n}\right)^n

(ID 4708)

$NTCP(D,v)=e^{-N_0v^{-k}P_n}$

NTCP(D,v)=e^{-N_0v^{-k}P_n}

(ID 4709)

$ t =\displaystyle\frac{ D_{eff} - TD_{50} }{ mTD_{50} }$

t =\displaystyle\frac{ D_{eff} - TD_{50} }{ mTD_{50} }

(ID 4846)

$ v_i =\displaystyle\frac{ V_i }{ V }$

v_i =\displaystyle\frac{ V_i }{ V }

(ID 4847)

$D_{eff}=\left(v_1D_1^{1/n}+v_2D_2^{1/n}\right)^n$

D_{eff}=\left(v_1D_1^{1/n}+v_2D_2^{1/n}\right)^n

(ID 4848)

$D_{eff}=\left(v_1D_1^{1/n}+v_2D_2^{1/n}+v_3D_3^{1/n}\right)^n$

D_{eff}=\left(v_1D_1^{1/n}+v_2D_2^{1/n}+v_3D_3^{1/n}\right)^n

(ID 4849)

$D_{eff}=\left(v_1D_1^{1/n}+v_2D_2^{1/n}+v_3D_3^{1/n}+v_4D_4^{1/n}\right)^n$

D_eff=(v_1D_1^1/n+v_2D_2^1/n+v_3D_3^1/n+v_4D_4^1/n)^n

(ID 8111)

$D_{eff}=\left(v_1D_1^{1/n}+v_2D_2^{1/n}+v_3D_3^{1/n}+v_4D_4^{1/n}+v_5D_5^{1/n}\right)^n$

D_eff=(v_1D_1^1/n+v_2D_2^1/n+v_3D_3^1/n+v_4D_4^1/n+v_5D_5^1/n)^n

(ID 8112)

$D_{eff}=D_i$

D_{eff}=D_i

(ID 9037)

$NTCP=1-\prod_i(1-NTCP_i)$

NTCP=1-\prod_i(1-NTCP_i)

(ID 9038)

$NTCP=1-(1-NTCP_1)(1-NTCP_2)$

NTCP=1-(1-NTCP_1)(1-NTCP_2)

(ID 9039)

Ejemplos

An lisis de la fracci n de tejido y su dosis

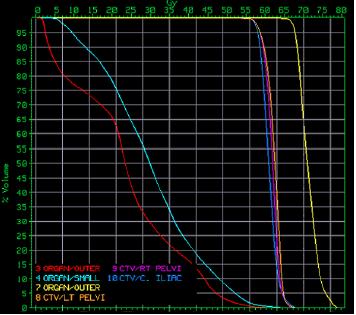
(ID 2714)

Modelo de Lyman-Kutcher-Burman (NTCP)

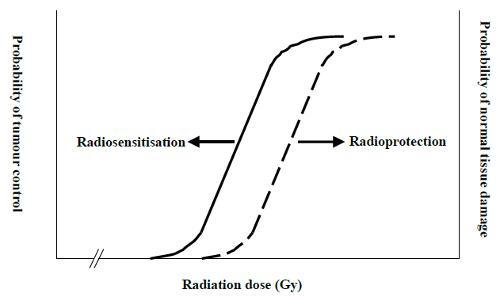
(ID 2715)

Factor DVH

Para poder estimar que tan bueno es un plan cuando la informaci n es 3D se puede proceder a sumar todos los voxeles que tienen la misma dosis y as generar un diagrama unidimensional:

(ID 1501)

Calculo del DVH

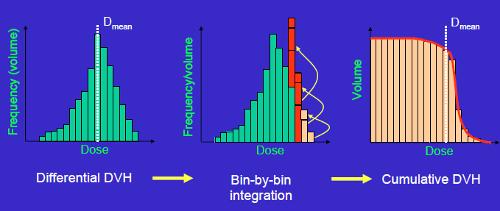
(ID 2718)

Probabilidad de complicaciones en tejido normal (NTCP)

(ID 1499)

Comparaci n TCP y NTCP

La siguiente gr fica muestra la distribuci n probabil stica de da o a rganos (linea azul) que da origen a la funci n de probabilidad de complicaciones en tejido normal (NTCP) (linea amarilla):

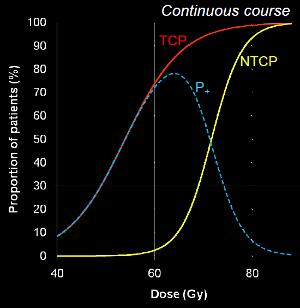
Adicionalmente se incluye la curva probabilidad de control de tumor TCP para compararla con la de TCP (linea roja).

El objetivo debe ser:

- lograr evitar irradiar rganos sensibles de modo de que la distribuci n de probable secuela sea m nima (linea azul) y con ello el NTCP (linea amarilla) sea lo mas plana posible solo aumentando para dosis mayores que la que se usara

- lograr que la linea de control de tumor TCP (linea roja) llegue a los mayores valores posibles a baja dosis asegurando asi el control del tumor

(ID 2713)

ID:(741, 0)