Usuario:
Efecto biológico
Definición 
El análisis del modelo L-Q entrega una serie de herramientas para estudiar el efecto biológico de la radiación e introducir medidas de efectividad biológica de los distintos tipos de radiación ionizante.
ID:(1495, 0)
Efecto Biológico para distinto Fraccionamiento
Imagen
Si se no se considera la multiplicación de las células se pueden determinar distintas combinaciones de dosis por tratamiento $d$ y numero de tratamientos (fraccionamiento) $n$ que arrojan una dosis radio-biológica equivalente. Las zonas equivalentes en una gráfica (n,d) se muestran a continuación para un $\alpha$ y $\beta$ especifico:
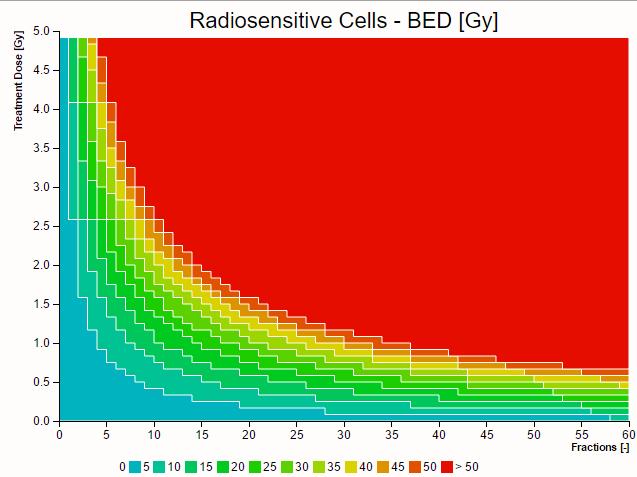
En el "Simulador Modelo L-Q y BED" se pueden estudiar distintos $\alpha$ y $\beta$. Cabe notar que las zonas de igual BED se desplazan según el tejido es radio-resistente o radio-sensible.
ID:(8849, 0)
Simulador modelo L-Q y BED
Nota
El siguiente simulador permite estudiar:
- las curvas L-Q para duplas de tejidos con distintas radiosensibilidades
- el efecto de fraccionar dosis sobre la dosis biologicamente equivalente
ID:(8745, 0)
Efecto Biológico
Descripción
Variables
Cálculos
a 
,
luego, seleccione la variable: 
a 
Cálculos
Variable
Dado
Calcule
Objetivo :
Ecuación
A utilizar
Ecuaciones
Ejemplos
El an lisis del modelo L-Q entrega una serie de herramientas para estudiar el efecto biol gico de la radiaci n e introducir medidas de efectividad biol gica de los distintos tipos de radiaci n ionizante.
(ID 1495)
La pregunta es cual es la combinaci n optima de numero $n$ y dosis por tratamiento $d$ que maximiza la destrucci n de las c lulas cancer genas.
Para determinar el optimo en numero $n$ y dosis de cada tratamiento $d$ hay que tener presente que c lulas sanas y cancer genas son irradiadas en la misma forma. Por ello debemos minimizar la fracci n de c lulas cancer genas y maximizar la fracci n de c lulas sanas que sobreviven. Por ello es importante considera la dependencia de la probabilidad de sobrevivencia de los factores $\alpha$ y $\beta$ seg n el tipo de c lula (ver gr fico). Matem ticamente se puede apreciar el efecto de la dosifcaci n si reescribimos la probabilidad de la forma
| $SF_n=e^{-\alpha BED }$ |
(ID 4021)
Si se re escribe la probabilidad del modelo L-Q como
| $SF_n=e^{-\alpha nd-\beta nd^2}$ |
por lo que se puede reescribir como una probabilidad que cumple la ley de Poissone
con
| $BED=nd\left(1+\displaystyle\frac{\beta d}{\alpha}\right)$ |
(ID 4696)
Si se supone que el BED puede ser aplicado en forma cl nica se tiene que planes de distinta dosis fraccional
| $BED=nd\left(1+\displaystyle\frac{\beta d}{\alpha}\right)$ |
serian equivalentes para cualquier combinaci n de
| $n_1d_1\left(1+\displaystyle\frac{d_1}{\alpha/\beta}\right)=n_2d_2\left(1+\displaystyle\frac{d_2}{\alpha/\beta}\right)$ |
(ID 3227)
Si se no se considera la multiplicaci n de las c lulas se pueden determinar distintas combinaciones de dosis por tratamiento $d$ y numero de tratamientos (fraccionamiento) $n$ que arrojan una dosis radio-biol gica equivalente. Las zonas equivalentes en una gr fica (n,d) se muestran a continuaci n para un $\alpha$ y $\beta$ especifico:
En el "Simulador Modelo L-Q y BED" se pueden estudiar distintos $\alpha$ y $\beta$. Cabe notar que las zonas de igual BED se desplazan seg n el tejido es radio-resistente o radio-sensible.
(ID 8849)
El siguiente simulador permite estudiar:
- las curvas L-Q para duplas de tejidos con distintas radiosensibilidades
- el efecto de fraccionar dosis sobre la dosis biologicamente equivalente
(ID 8745)
ID:(737, 0)