Un ejemplo de datos de sobre-vivencia representa la siguiente tabla de dosis en Gray y tasa de sobre-vivencia de c lulas:

Dosis [Gy] | Sobrevivientes

---------------|:------------------:

0 | 1.00000

1 | 0.90937

2 | 0.78820

3 | 0.65116

4 | 0.51273

5 | 0.38481

6 | 0.27527

7 | 0.18768

8 | 0.12197

9 | 0.07555

10 | 0.04460

(ID 7401)

Si se gr fica la fracci n de c lulas que sobrevive en funci n de la dosis aplicada se obtiene una curva del tipo:

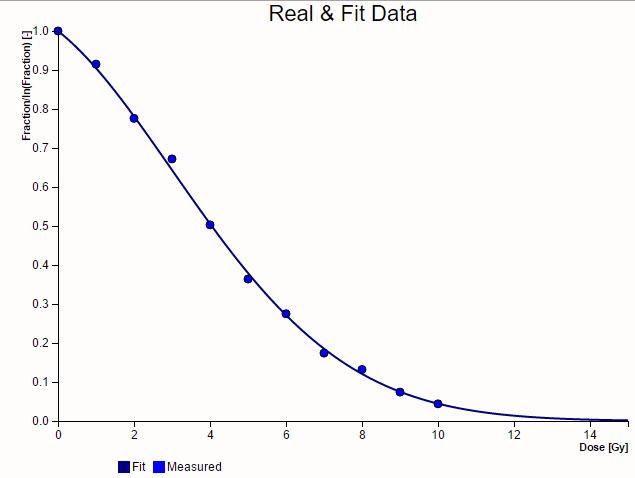
(ID 2709)

Si se gr fica la fracci n de c lulas que sobreviven con escala logar tmica se obtiene una gr fica de la forma

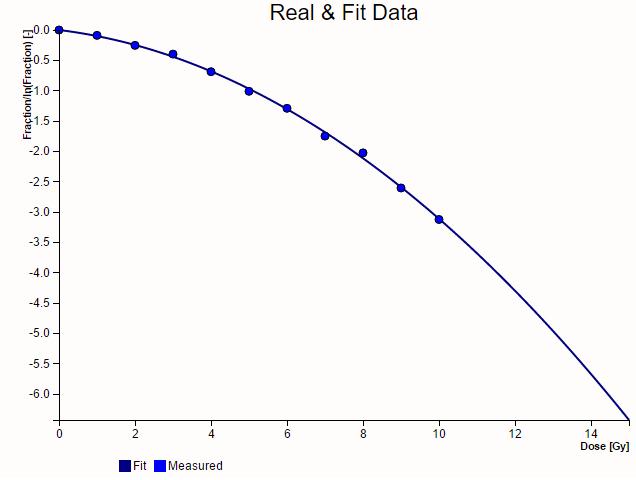
en donde se reconoce la forma de una "par bola negativa".

En otras palabras la fracci n de sobre-vivencia se puede expresar mediante una funci n exponencial en que su exponente es un polinomio de segundo orden de la dosis.

$SF=e^{polinomio,en,la,dosis}$

Sin embargo, como en el caso de dosis nula la tasa de sobre-vivencia debe ser igual a 1.0, se tiene para dosis nula el polinomio debe ser nulo. Por ello el polinomio no tiene un factor constante, solo un factor lineal y otro cuadr tico en la dosis. Por ello el modelo que se emplea se denomina el modelo lineal cuadr tico o por sus ciclas en ingles, el modelo LQ (linear-quadratic).

(ID 1977)

Los factores \alpha y \beta se pueden calcular tomando los logaritmos naturales de las tasas de sobre-vivencia y sus respectivas dosis y realizando un regresi n para una par bola que pasa por el origen (0,0):

(ID 7384)

Si se gr fica la tasa de sobre-vivencia para tejidos de distintos rganos se observa que existen distintos niveles de radio-sensibilidad o radio-resistencia:

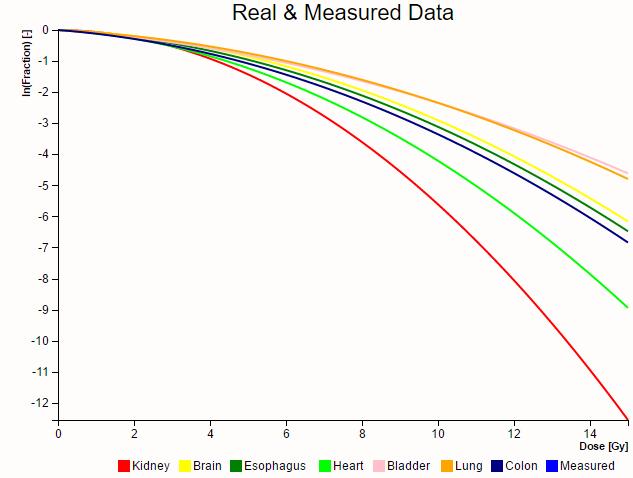
(ID 2707)

El siguiente simulador permite estudiar:

- las curvas L-Q para duplas de tejidos con distintas radiosensibilidades

- el efecto de fraccionar dosis sobre la dosis biologicamente equivalente

(ID 8745)

El factor \alpha corresponde a la pendiente inicial mientras que el factor \beta domina para dosis mayores.
Por ello tejidos con una relaci n \alpha/\beta grande (\alpha/\beta entre 5 y 20) tienden a decrecer a baja dosis m s pero luego menos que relaciones peque as (\alpha/\beta entre 1 y 5):

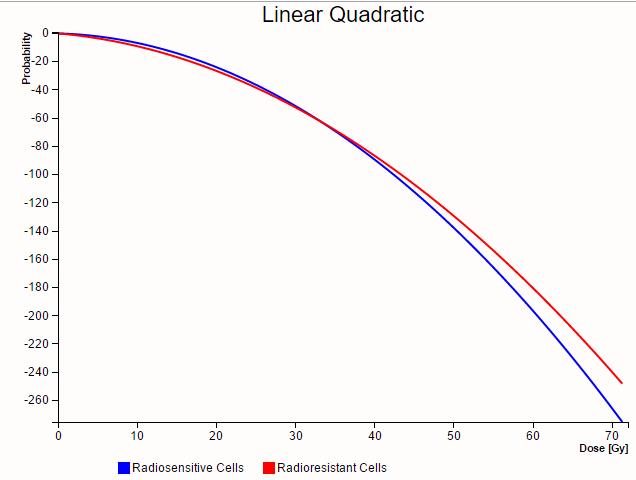
Por ello se habla de que tejidos con gran \alpha/\beta son radio-resistentes y con menor \alpha/\beta que son radio-sensibles.

(ID 2706)