Solving problems with networks of equations
Storyboard 
A simpler approach is to use the same network of equations used to design the resolution strategy to perform the actual calculation.
In this case, the given variables are associated with those in the model by entering their value and units, and then conversion is performed. Next, equations and variables to be calculated are chosen by clicking on the graph of the network. Finally, the unit in which the result should be delivered is selected, and the final conversion is carried out.
In this scenario, the only risk, aside from making errors in model selection, is erroneously associating the given variable with the model variable. Hence, it is important to understand what the model describes in order to correctly interpret the problem.
ID:(1936, 0)
Access to the Equation Networks application
Image 
To enter the Equation Networks application, you can use the main page or via the Work menu under Learning the Buchow Svensson Method and Instructions.

ID:(14425, 0)
Generation and analysis of a Problem
Image 
To enter the Equations Network application, you can use the main page or via the Work menu under Learning the Buchow Svensson Method and Instructions.
The method allows using the same network with which the solution strategy is determined to perform the calculation of the searched variable.
ID:(14426, 0)
Identification of the model and the given variables
Image 
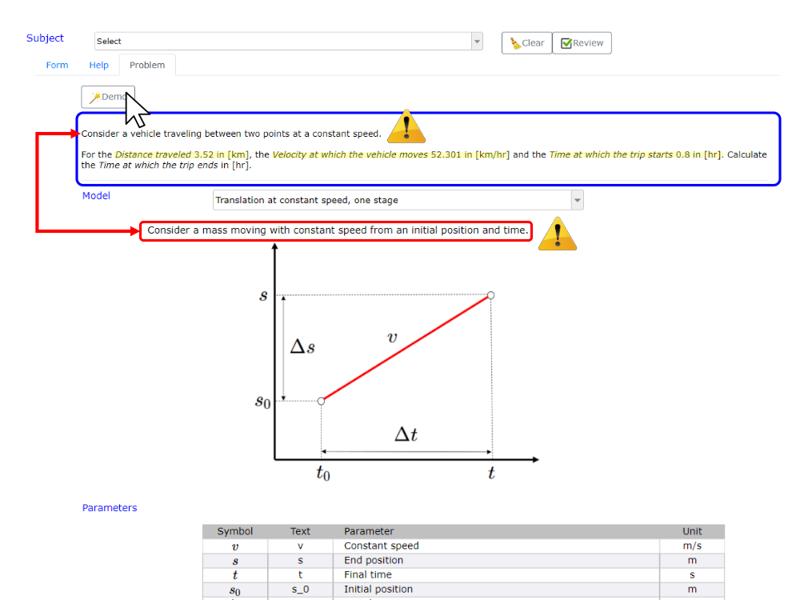
First, the Problem must be studied and identified based on the restrictions it has, the variables it delivers and the variable it seeks.
Once the model is loaded, those that correspond to the given data must be identified in the list of variables.
Once the variables have been identified, they must be located in the network of equations. An effective help is to use the search function of the browser (Ctrl + f). Entering the symbol as listed under Text lights up (presents a bright yellow background) the variable in the network.
ID:(14427, 0)
Load the variables
Image 
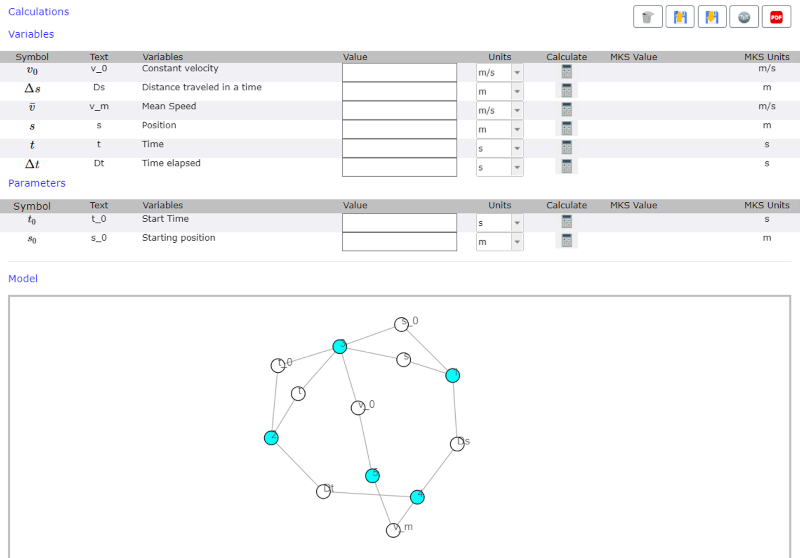
For each variable, locate the node in the white network and click on it.
The node becomes a bright light green color and a line appears at the bottom of the network with the name of the variable, its MKS unit and a field to enter its value and unit.
ID:(14428, 0)
Convert the units of variables
Image 
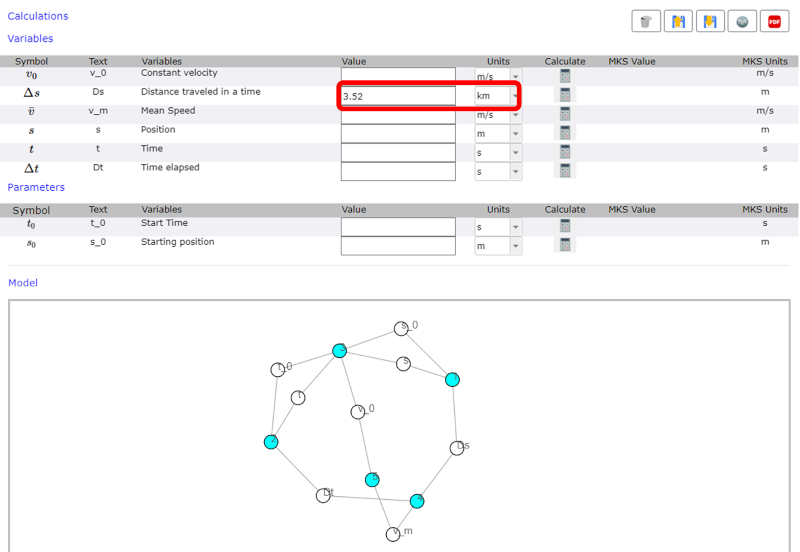
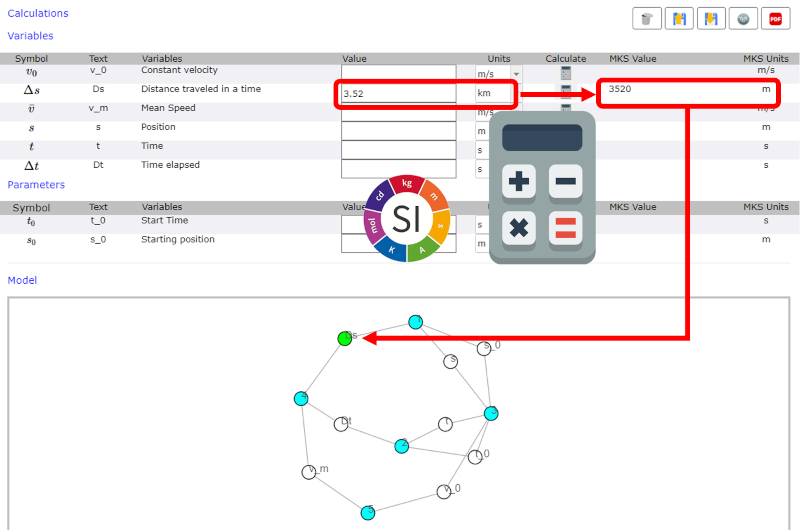
Once the line for each variable is generated, the value of the variable must be entered.
Since the variable already has its unit defined, all possible units of this type are listed.
After selecting the unit, the calculator icon is pressed, which generates the value converted to an MKS unit.
ID:(14429, 0)
System prepared to carry out the calculations
Image 
At the end of the first step, there is a network of equations in which the variables whose values are given are observed.
Additionally, there is a list of variables with their original values and units and the corresponding MKS values.
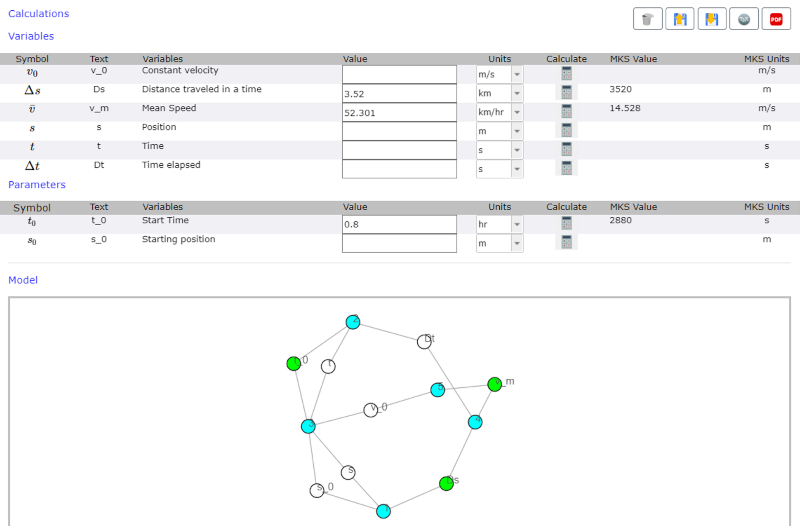
ID:(14430, 0)
Identification of equation that can be calculated
Image 
To calculate the result sought, the node of the result variable is located and the equations that allow its calculation are reviewed.
If an equation is found for which the remaining variables have values (green nodes), the calculation can be carried out.
If none of the equations can be applied at this stage, the missing variables should be studied, identifying an equation that allows their calculation (all of the challenging variables have data values). In this case, this intermediate variable is calculated and with it the final calculation is made.
In some cases it is necessary to work with multiple calculations of intermediate variables.
When finding an equation, click on the node of the equation. If it is feasible to perform the calculation, the node turns dark blue and a line with the selected equation is added at the end of the window. If it is not possible to use the calculation of the equation, an error is issued.
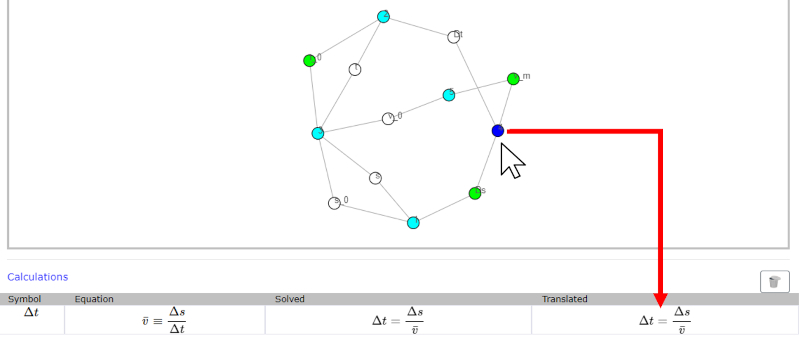
Let\'s remember that:
The calculation can only be performed if there is only one unknown variable (white node) and all other variables are known (green or orange nodes).
ID:(14431, 0)
Calculation of the intermediate variable
Image 
Once the equation has been successfully marked, click on the variable to be calculated. This must necessarily be represented by a white node which means that its value is still unknown.
The action triggers that the value is calculated and the node changes from white to orange.
The value calculated with the selected equation appears in the lower right field. This value is in MKS.
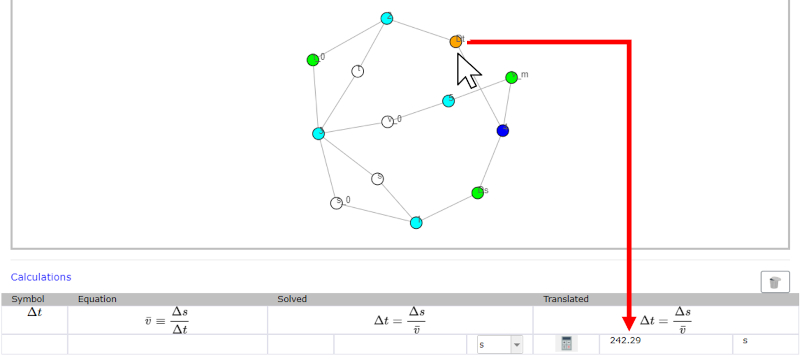
ID:(14432, 0)
Final Equation Identification
Image 
Once all the intermediate variables have been calculated, the equation can be selected to calculate the result sought.
When finding the equation, click on the node of the equation. If it is feasible to perform the calculation, the node turns dark blue and a line with the selected equation is added at the end of the window. If it is not possible to use the calculation of the equation, an error is issued.
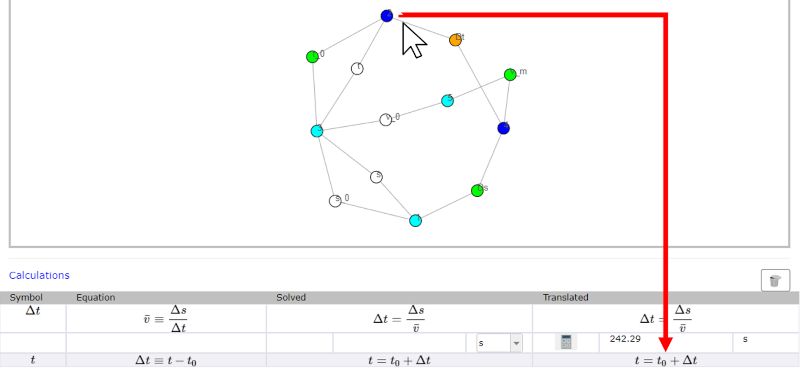
ID:(14433, 0)
Calculation of the final result
Image 
Once the equation has been successfully marked, click on the variable to be calculated. This must necessarily be represented by a white node which means that its value is still unknown.
The action triggers that the value is calculated and the node changes from white to orange.
The value calculated with the selected equation appears in the lower right field. This value is in MKS.
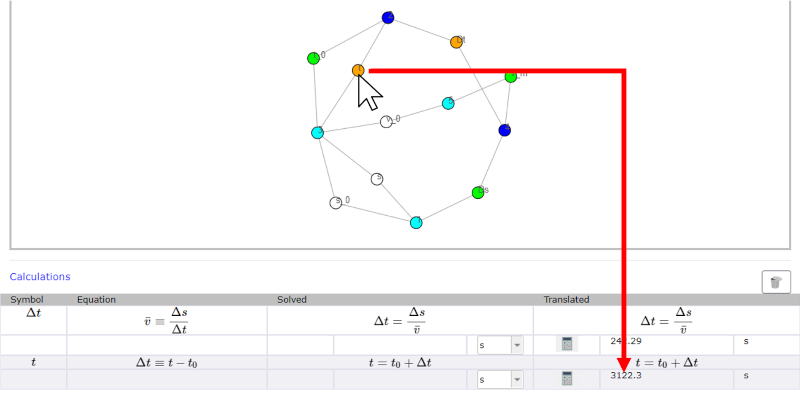
ID:(14434, 0)
Convert result to required unit
Image 
The result calculated up to this point is in the units of the system that has been chosen to work (example MKS).
If the result is requested in different units, it is necessary to convert the result of the calculation to the required units.
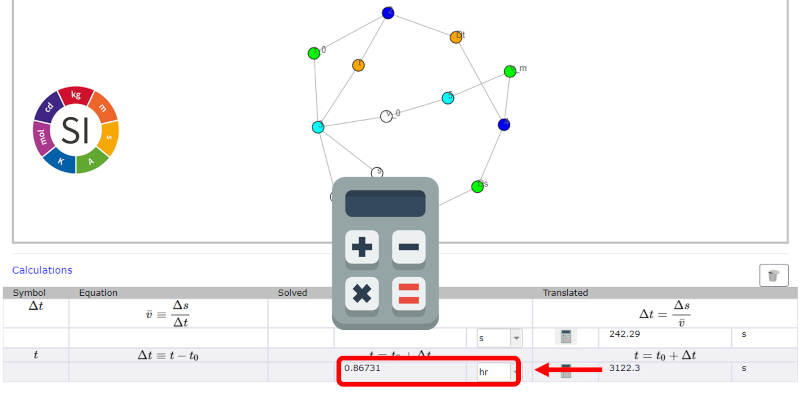
To do this, select the desired unit and press the calculator icon, which directly transforms the result.
Note: to document the calculation it is convenient to carry out this last calculation even when there is no change of units.
ID:(14435, 0)
