Digital Problem solving without help
Storyboard 
The systematic problem-solving via a form can also be electronically documented.
In the manual case, there is no assistance provided for unit conversions, equation solving, associating given variables with equation variables, or calculating intermediate and final variables. Only a list of equations and variables associated with the model being employed is included.
Despite the lack of assistance in unit conversion, equation solving, and variable calculation, examples of programs that can aid in these actions are provided.
It's important to note that under 'Problem Solving with Assistance,' a version of the form that performs conversions, solves equations, and conducts calculations for the user is demonstrated.
ID:(1934, 0)
Access to the application Form without assistance
Concept 
To enter the application Form without Assistance you can use the main page or via the Work menu under Learning Buchow Svensson Method and Instructions

Do not forget that this method only allows documentation, the conversions and resolutions of the equations being an activity carried out by the user. The version with assistance includes this type of help while the Network version allows solving directly from the network with which the strategy is defined.
ID:(14400, 0)
Problem generation and analysis
Concept 
The application includes a problem generator. As long as a Theme is not selected, a Demo can be generated with which all the aids have been built. This allows the user to replicate what is explained in the help. If a topic is chosen, multiple problems can be generated to exercise.
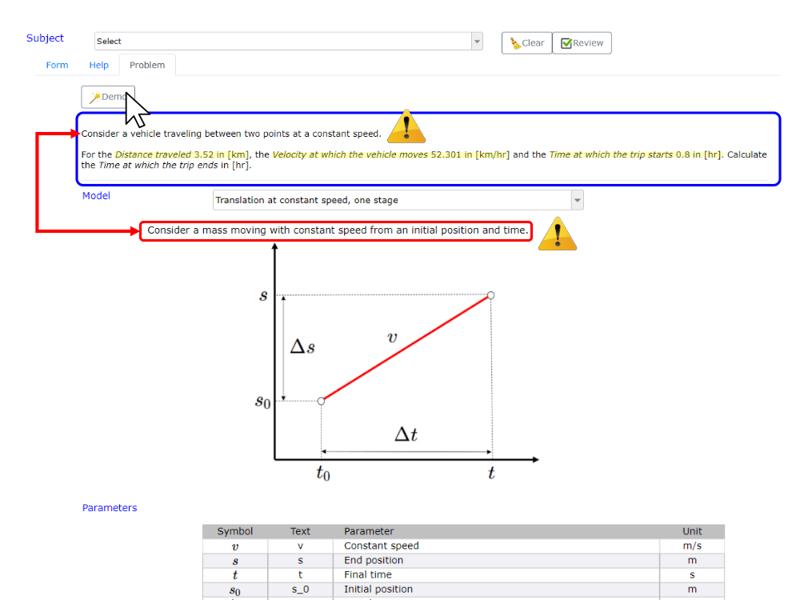
To solve the exercise, we first proceed to identify the model with which it can be addressed. Selecting this allows us to analyze the network of equations valid in this case, identify the variables given to us and find the best solution strategy. The technique is explained in its own narrative in more detail.
ID:(14401, 0)
Convert variable value to MKS
Concept 
As it is necessary that all the variables are in the same system of units, the corresponding transformation must be carried out.
To do this, the value is converted and the result of the calculation is entered in the corresponding column of the form. In case the value is already in the selected unit system, its value is simply written again.
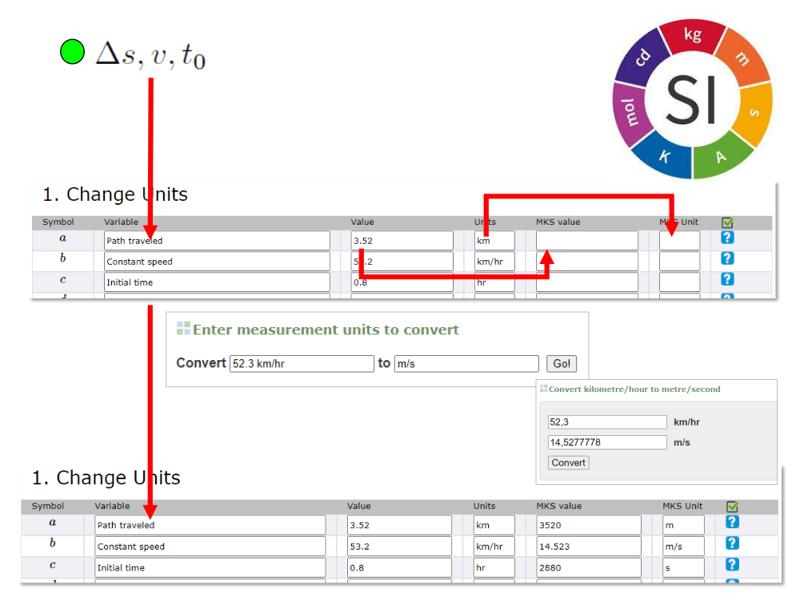
This can be done either with the corresponding conversions or if they are not available using applications such as https://www.convertunits.com/.
In this example the MKS unit system (meters-kilograms-seconds) is being used, but others can also be used.
ID:(14402, 0)
Identify equation
Concept 
Based on the network of equations and the given variables, the equation that can be used to calculate the intermediate variables must be identified.
It is to remember that equations can only be used in which there is only one unknown variable (blank node) and all the rest are given (green node) or have already been calculated (orange node).
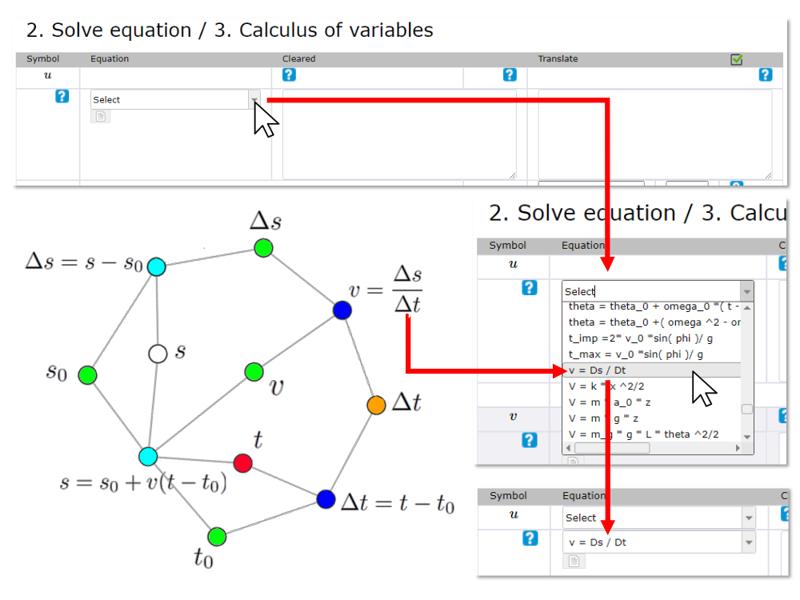
It should be noted that:
Equations and their variables come from the system form and the symbols used may coincide with those of the model variables without corresponding to equivalent variables.
That is why it is key:
Only associate variables of the equations with those of the formulas based on whether they have the equivalent physical meaning and not by similarity of symbols used.
.
ID:(14403, 0)
Identify intermediate variable
Concept 
Once the equation has been chosen, the variable can be chosen.
It is important that this physically corresponds to the intermediate variable to be calculated and is not chosen simply by symbol similarity.
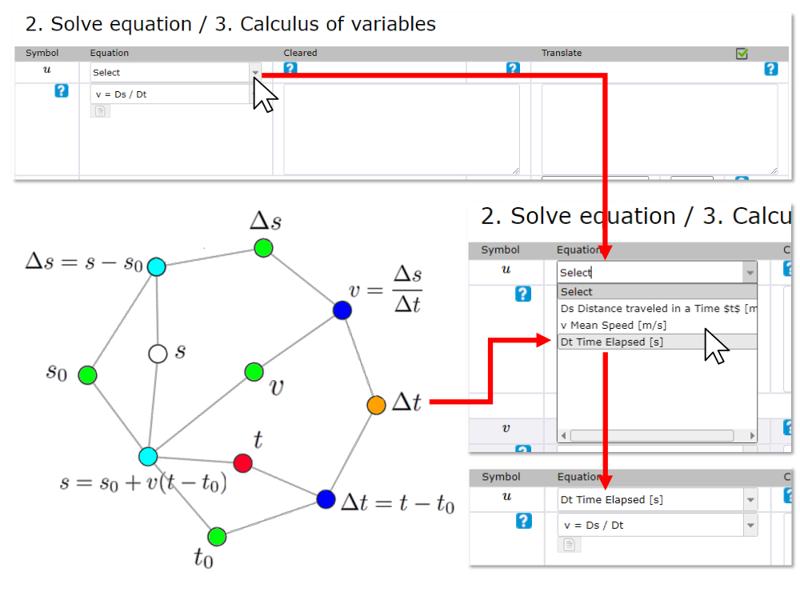
An effective check that it is the searched variable is the coincidence in the units.
ID:(14404, 0)
Solve the equation
Concept 
The solution of the equation can be obtained and written directly in the field next to the original equation.
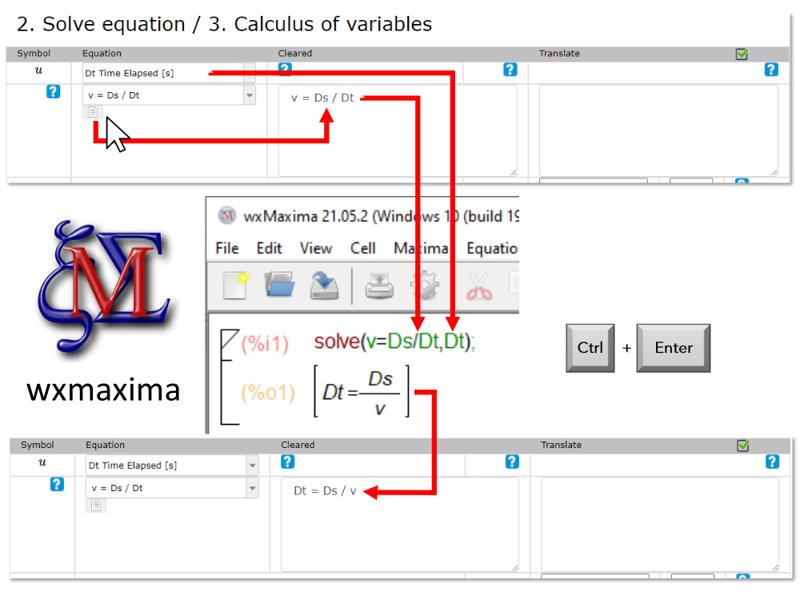
If you are working with a wxmaxima type program, you can press the button below the original equation. This copies the formula to the window next to the equation. In this way, the formula can be copied directly to the wxmaxima work area, avoiding transcription errors.
Once the solution is calculated it can be copied back into the field next to the equation.
ID:(14405, 0)
Translate the equation
Concept 
It must be indicated for each variable of the equation to which variable of the problem it corresponds. To do this, you must understand the physical meaning of each variable in the equation and understand which variable of the problem it corresponds to.
It is key to base it on the meaning and not on the similarity of the symbols used since this similarity can be coincidental.
Seeking to define the variables of the problem based on those of the equations is many times impossible both because of the fact that different equations can use the same symbols for variables that physically mean different things. On the other hand, the same equation can be used on multiple occasions for different variables of the problem.
For all these reasons it is necessary for each application of an equation to establish an equivalence with variables of the problem and thus translate the equation.
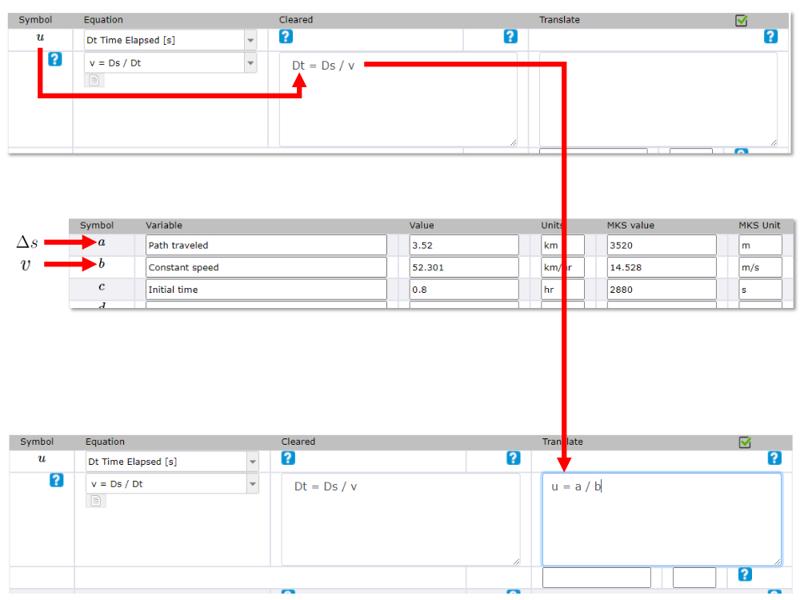
In the case of the form, it is assumed that the different variables given are assigned the letters a, b, c, etc., while the intermediate variables are assigned the letters u, v, w and for the final result the letter z. With this, the equation must be rewritten as a function of these variables.
ID:(14406, 0)
Calculate the intermediate variable
Concept 
After the translation, it was defined exactly which variable should assume which value and the calculation of the intermediate variable can be performed directly.
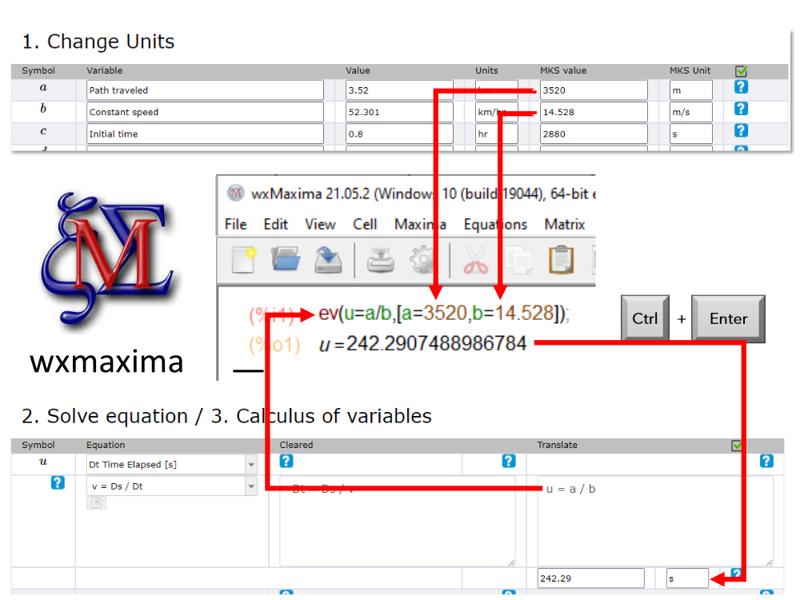
An alternative to carry out the calculation is the use of wxmaxima using the ev function that allows entering the formula and in a list the variables and their values.
ID:(14407, 0)
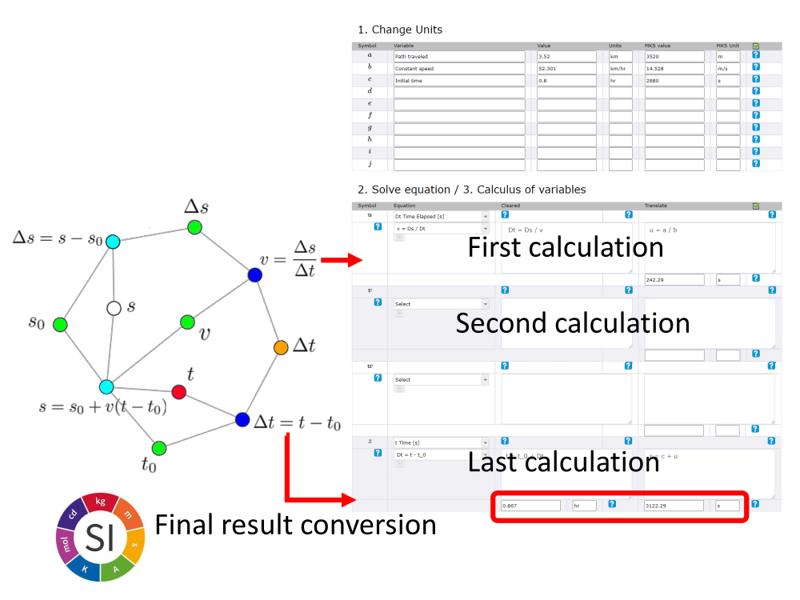
Calculation structure
Concept 
The calculations are entered to generate the intermediate variables u, v and w. The last calculation is always entered as the final variable z. This is because the only block that has the unit conversion is this one. If the problem only considers a calculation, only the calculation is entered at the end of the table, generating the final variable z.
ID:(14408, 0)
Equation for the final result
Concept 
The calculations are entered to generate the intermediate variables u, v and w. The last calculation is always entered as the final variable z. This is because the only block that has the unit conversion is this one. If the problem only considers a calculation, only the calculation is entered at the end of the table, generating the final variable z.
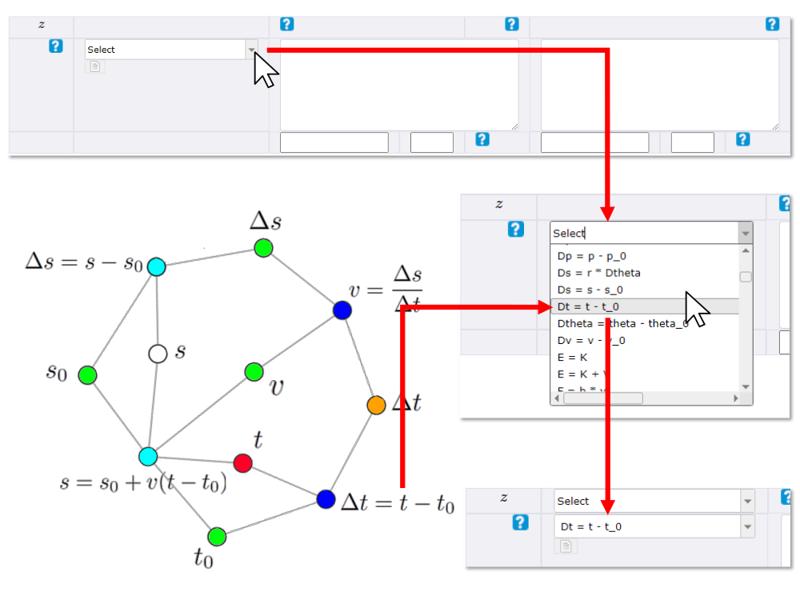
ID:(14409, 0)
End result variable
Concept 
Once the equation for the final calculation is selected, the variable that corresponds to the final result sought must be identified.
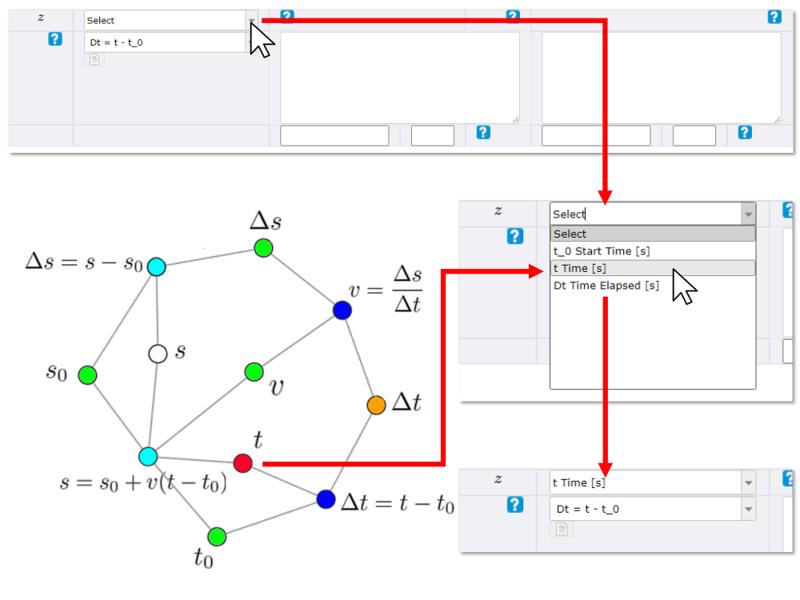
To ensure that the variable is correct, it is recommended to verify that the units of the selected variable correspond to those of the final result.
ID:(14410, 0)
Solve the final equation
Concept 
In order to use the final equation, like those for calculating the intermediate variables, we must solve them based on the variable that corresponds to the final result.
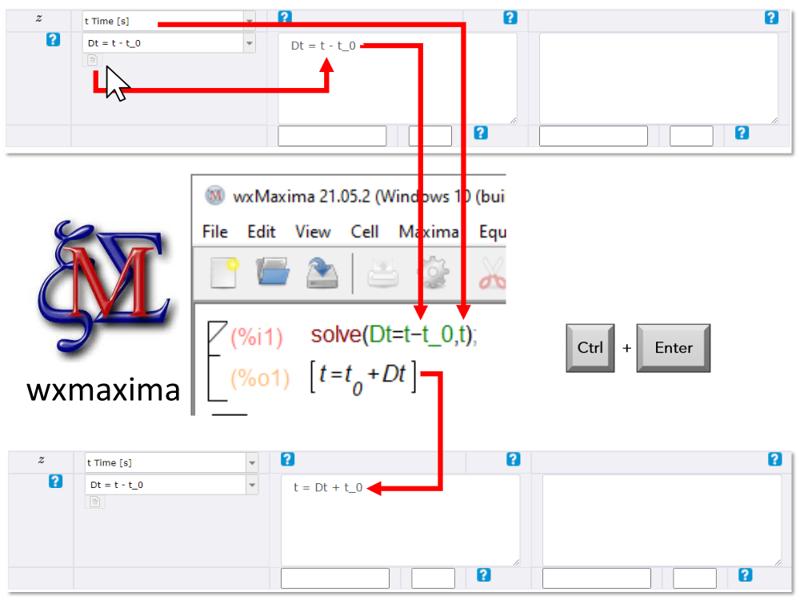
If you are working with a wxmaxima type program, you can press the button below the original equation. This copies the formula to the window next to the equation. In this way, the formula can be copied directly to the wxmaxima work area, avoiding transcription errors.
Once the solution is calculated it can be copied back into the field next to the equation.
ID:(14411, 0)
Calculation of the final result in MKS
Concept 
As in the previous cases, the value of the result in MKS must be calculated with the translated equation.
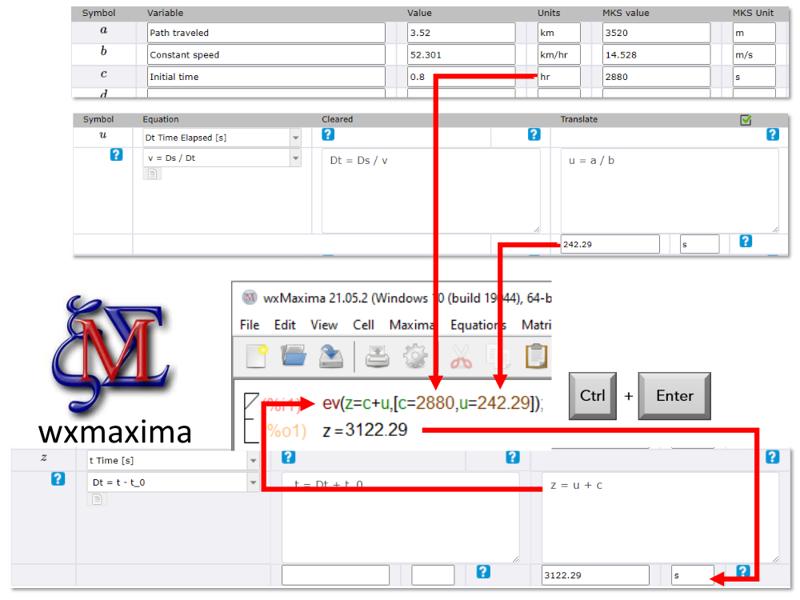
An alternative to carry out the calculation is the use of wxmaxima using the ev function that allows entering the formula and in a list the variables and their values.
ID:(14412, 0)
Convert result to required unit
Concept 
The result calculated up to this point is in the units of the system that has been chosen to work (example MKS).
If the result is requested in different units, it is necessary to convert the result of the calculation to the required units.
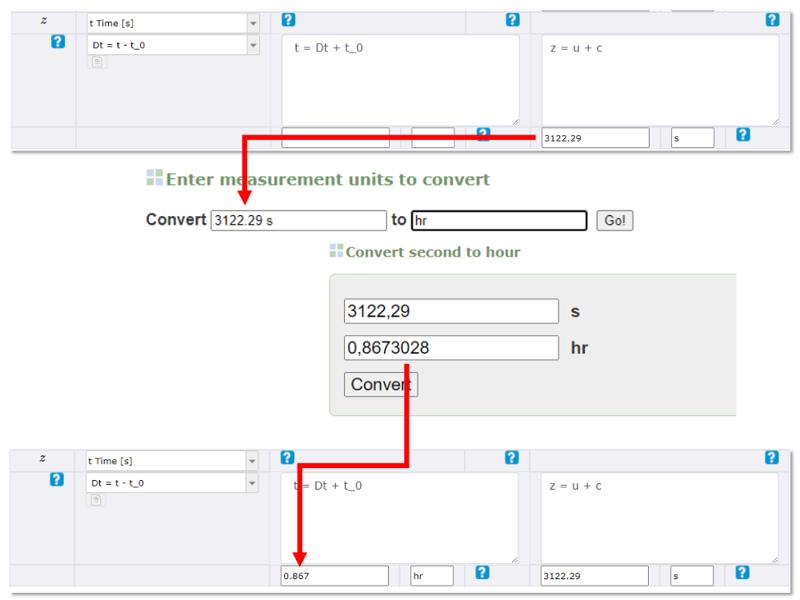
This can be done either with the corresponding conversions or if they are not available using applications such as https://www.convertunits.com/.
In this example the MKS unit system (meters-kilograms-seconds) is being used, but others can also be used.
ID:(14413, 0)
