Utilisateur:
Loi de Gay-Lussac
Storyboard 
La loi de Gay-Lussac établit que le quotient de a pression ($p$) par a température absolue ($T$) reste constant lorsque le volume et la quantité de matière sont maintenus constants.
Cela signifie que a pression ($p$) varie de manière proportionnelle à A température absolue ($T$).
ID:(1474, 0)
Mécanismes
Concept
La loi de Gay-Lussac stipule que la pression d'un gaz est directement proportionnelle à sa température lorsque le volume reste constant. Cela signifie que, à mesure que la température d'un gaz augmente, sa pression augmente également, à condition que le volume ne change pas. Inversement, si la température diminue, la pression diminue aussi. Cette relation est cruciale pour comprendre le comportement des gaz dans des récipients fermés, où une augmentation de la température entraîne une augmentation de la pression et une diminution de la température entraîne une diminution de la pression.
ID:(15256, 0)
Variation de pression et de température
Concept
A pression ($p$) se produit lorsque les particules de gaz entrent en collision avec la surface du conteneur de gaz. Chaque collision transmet un moment égal à deux fois a masse molaire ($m$) par a vitesse moyenne d'une particule ($\bar{v}$). De plus, il est important de considérer le flux de particules vers la surface, qui dépend de a concentration de particules ($c_n$) mais aussi de a vitesse moyenne d'une particule ($\bar{v}$) avec lequel elles se déplacent. Ainsi,
$p \propto c_n v \cdot m v = c_n m v^2$
Le flux de particules et la transmission du moment sont représentés dans le graphique ci-dessous :
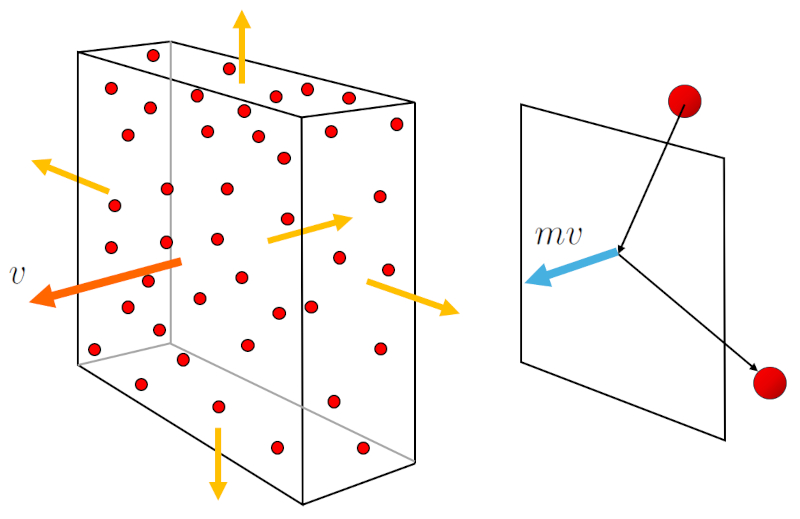
De plus, a masse molaire ($m$) par a vitesse moyenne d'une particule ($\bar{v}$) au carré est proportionnel à A énergie d'une molécule ($E$), qui est lui-même proportionnel à A température absolue ($T$) :
$p \propto c_n mv^2 \propto E \propto T$
Dans ce cas, lorsque le volume ($V$) et le nombre de particules ($N$) sont constants, a concentration de particules ($c_n$) est également constant.
ID:(15690, 0)
Relation température/pression
Description
Dans un gaz, lorsque le volume ($V$) et le nombre de particules ($N$) sont maintenus constants, on observe que a pression ($p$) et a température absolue ($T$) varient de manière proportionnelle. Lorsque a température absolue ($T$) diminue, a pression ($p$) diminue également, et vice versa,
$p \propto T$
comme illustré dans le graphique suivant :
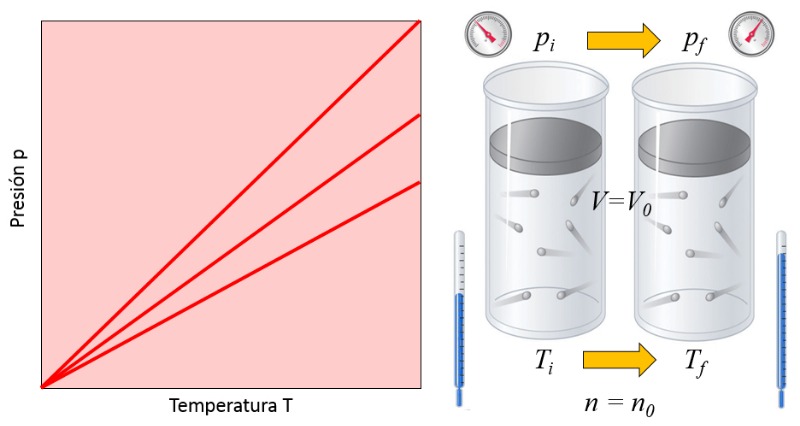
La loi de Gay-Lussac [1] stipule que lorsque le volume ($V$) et le nombre de particules ($N$) sont maintenus constants, a pression ($p$) et a température absolue ($T$) sont directement proportionnels.
Cela s'exprime avec a constante de la loi de Gay Lussac ($C_g$) comme suit :
| $\displaystyle\frac{ p }{ T } = C_g$ |
[1] "Mémoire sur la combinaison des substances gazeuses les unes avec les autres" (Mémoire sur la combinaison des substances gazeuses les unes avec les autres), Joseph Louis Gay-Lussac, Annales scientifiques de l'É.N.S. 3e série, tome 3 (1886)
ID:(9530, 0)
Joseph Louis Gay Lussac
Description
Joseph Louis Gay-Lussac était un chimiste et physicien français qui a vécu de 1778 à 1850. Il a apporté d'importantes contributions dans les domaines de la chimie et des lois des gaz. Gay-Lussac a réalisé de nombreuses expériences et recherches, notamment sur les propriétés des gaz, et a formulé plusieurs lois et principes importants. L'une de ses réalisations remarquables a été la découverte de la loi des volumes combinés, connue sous le nom de loi de Gay-Lussac. Il a également contribué à l'étude de l'électrolyse, à la mesure de la température et à la compréhension des réactions chimiques. Le travail de Gay-Lussac a eu une grande influence sur le développement de la chimie et a jeté les bases des théories chimiques modernes.
ID:(1658, 0)
Changement d'état d'un gaz parfait selon la loi de Gay Lussac
Concept
La loi de Gay-Lussac stipule que lorsque ERROR:5226,0 et le nombre de particules ($N$) sont maintenus constants, le rapport de a pression ($p$) à A température absolue ($T$) est égal à A constante de la loi de Gay Lussac ($C_g$) :
| $\displaystyle\frac{ p }{ T } = C_g$ |
Cela signifie que si un gaz passe d'un état initial (a pression à l'état initial ($p_i$) et a température à l'état initial ($T_i$)) à un état final (a pression à l'état final ($p_f$) et a température à l'état final ($T_f$)) en maintenant a pression ($p$) et le nombre de particules ($N$) constants, la loi de Gay-Lussac doit toujours être respectée :
$\displaystyle\frac{p_i}{T_i}=C_g=\displaystyle\frac{p_f}{T_f}$
Par conséquent, on a :
| $\displaystyle\frac{ p_i }{ T_i }=\displaystyle\frac{ p_f }{ T_f }$ |
ID:(15691, 0)
Loi de Gay-Lussac
Modèle
La loi de Gay-Lussac établit que le quotient de 5224 par 5177 reste constant lorsque le volume et la quantité de matière sont maintenus constants. Cela signifie que 5224 varie de manière proportionnelle à 5177.
Variables
Calculs
à 
,
puis, sélectionnez la variable: 
à 
Calculs
Variable
Donnée
Calculer
Cible :
Équation
À utiliser
Équations
La loi de Gay-Lussac stipule que lorsque ERROR:5226,0 et le nombre de particules ($N$) sont maintenus constants, le rapport de a pression ($p$) A température absolue ($T$) est gal a constante de la loi de Gay Lussac ($C_g$) :
| $\displaystyle\frac{ p }{ T } = C_g$ |
Cela signifie que si un gaz passe d'un tat initial (a pression à l'état initial ($p_i$) et a température à l'état initial ($T_i$)) un tat final (a pression à l'état final ($p_f$) et a température à l'état final ($T_f$)) en maintenant a pression ($p$) et le nombre de particules ($N$) constants, la loi de Gay-Lussac doit toujours tre respect e :
$\displaystyle\frac{p_i}{T_i}=C_g=\displaystyle\frac{p_f}{T_f}$
Par cons quent, on a :
| $\displaystyle\frac{ p_i }{ T_i }=\displaystyle\frac{ p_f }{ T_f }$ |
(ID 3490)
Exemples
La loi de Gay-Lussac stipule que la pression d'un gaz est directement proportionnelle sa temp rature lorsque le volume reste constant. Cela signifie que, mesure que la temp rature d'un gaz augmente, sa pression augmente galement, condition que le volume ne change pas. Inversement, si la temp rature diminue, la pression diminue aussi. Cette relation est cruciale pour comprendre le comportement des gaz dans des r cipients ferm s, o une augmentation de la temp rature entra ne une augmentation de la pression et une diminution de la temp rature entra ne une diminution de la pression.
(ID 15256)
A pression ($p$) se produit lorsque les particules de gaz entrent en collision avec la surface du conteneur de gaz. Chaque collision transmet un moment gal deux fois a masse molaire ($m$) par a vitesse moyenne d'une particule ($\bar{v}$). De plus, il est important de consid rer le flux de particules vers la surface, qui d pend de a concentration de particules ($c_n$) mais aussi de a vitesse moyenne d'une particule ($\bar{v}$) avec lequel elles se d placent. Ainsi,
$p \propto c_n v \cdot m v = c_n m v^2$
Le flux de particules et la transmission du moment sont repr sent s dans le graphique ci-dessous :
De plus, a masse molaire ($m$) par a vitesse moyenne d'une particule ($\bar{v}$) au carr est proportionnel a énergie d'une molécule ($E$), qui est lui-m me proportionnel a température absolue ($T$) :
$p \propto c_n mv^2 \propto E \propto T$
Dans ce cas, lorsque le volume ($V$) et le nombre de particules ($N$) sont constants, a concentration de particules ($c_n$) est galement constant.
(ID 15690)
Dans un gaz, lorsque le volume ($V$) et le nombre de particules ($N$) sont maintenus constants, on observe que a pression ($p$) et a température absolue ($T$) varient de mani re proportionnelle. Lorsque a température absolue ($T$) diminue, a pression ($p$) diminue galement, et vice versa,
$p \propto T$
comme illustr dans le graphique suivant :
La loi de Gay-Lussac [1] stipule que lorsque le volume ($V$) et le nombre de particules ($N$) sont maintenus constants, a pression ($p$) et a température absolue ($T$) sont directement proportionnels.
Cela s'exprime avec a constante de la loi de Gay Lussac ($C_g$) comme suit :
| $\displaystyle\frac{ p }{ T } = C_g$ |
[1] "M moire sur la combinaison des substances gazeuses les unes avec les autres" (M moire sur la combinaison des substances gazeuses les unes avec les autres), Joseph Louis Gay-Lussac, Annales scientifiques de l' .N.S. 3e s rie, tome 3 (1886)
(ID 9530)
Joseph Louis Gay-Lussac tait un chimiste et physicien fran ais qui a v cu de 1778 1850. Il a apport d'importantes contributions dans les domaines de la chimie et des lois des gaz. Gay-Lussac a r alis de nombreuses exp riences et recherches, notamment sur les propri t s des gaz, et a formul plusieurs lois et principes importants. L'une de ses r alisations remarquables a t la d couverte de la loi des volumes combin s, connue sous le nom de loi de Gay-Lussac. Il a galement contribu l' tude de l' lectrolyse, la mesure de la temp rature et la compr hension des r actions chimiques. Le travail de Gay-Lussac a eu une grande influence sur le d veloppement de la chimie et a jet les bases des th ories chimiques modernes.
(ID 1658)
La loi de Gay-Lussac stipule que lorsque ERROR:5226,0 et le nombre de particules ($N$) sont maintenus constants, le rapport de a pression ($p$) A température absolue ($T$) est gal a constante de la loi de Gay Lussac ($C_g$) :
| $\displaystyle\frac{ p }{ T } = C_g$ |
Cela signifie que si un gaz passe d'un tat initial (a pression à l'état initial ($p_i$) et a température à l'état initial ($T_i$)) un tat final (a pression à l'état final ($p_f$) et a température à l'état final ($T_f$)) en maintenant a pression ($p$) et le nombre de particules ($N$) constants, la loi de Gay-Lussac doit toujours tre respect e :
$\displaystyle\frac{p_i}{T_i}=C_g=\displaystyle\frac{p_f}{T_f}$
Par cons quent, on a :
| $\displaystyle\frac{ p_i }{ T_i }=\displaystyle\frac{ p_f }{ T_f }$ |
(ID 15691)
(ID 15315)
ID:(1474, 0)