Utilisateur:


Loi de Boyle-Mariotte
Storyboard

La loi de Boyle-Mariotte établit que le produit de a pression ($p$) et le volume ($V$) d'un gaz reste constant lorsque la température absolue et la quantité de matière ne varient pas.

Cela signifie que a pression ($p$) varie de manière inversement proportionnelle à Le volume ($V$).

>Modèle

ID:(1472, 0)


Mécanismes
Concept

La loi de Boyle-Mariotte, également connue sous le nom de loi de Boyle, décrit la relation inverse entre la pression et le volume d'un gaz à température constante. Elle stipule que, pour une quantité fixe de gaz, lorsque la température est maintenue constante, la pression du gaz augmente à mesure que le volume diminue, et vice-versa. Cela signifie que si vous compressez un gaz en réduisant son volume, sa pression augmentera proportionnellement, et si vous augmentez le volume, la pression diminuera proportionnellement. Cette relation est fondamentale pour comprendre le comportement des gaz et s'exprime mathématiquement par le produit de la pression et du volume étant une constante pour une quantité de gaz donnée à température constante.

ID:(15254, 0)


Variation de volume et de pression
Concept

A pression ($p$) est généré lorsque les particules de gaz entrent en collision avec la surface du contenant de gaz. Comme a température absolue ($T$) est constant, l'énergie des particules ne varie pas et les chocs de celles-ci avec les surfaces du contenant de gaz ne varieront pas dans le transfert d'impulsion. Cependant, le nombre d'impacts dépend du nombre de particules près de la surface, qui à son tour est proportionnel au a concentration de particules ($c_n$) du gaz.



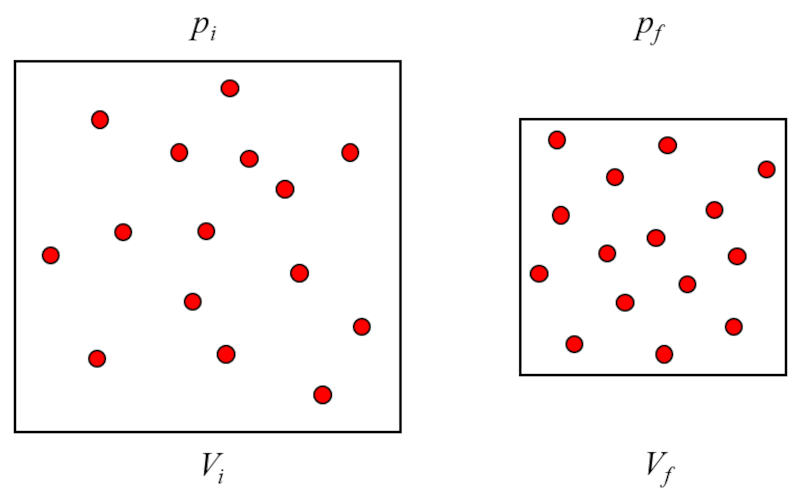
D'autre part, la densité est inversement proportionnelle à Le volume ($V$), ce qui conduit à la relation suivante :

$p \propto c_n \propto \displaystyle\frac{1}{V}$

ID:(9602, 0)


Relation volume et pression
Description

Dans un gaz, si à la fois a température absolue ($T$) et le nombre de particules ($N$) sont maintenus constants, on observe que le volume ($V$) et a pression ($p$) varient de manière inversement proportionnelle. Chaque fois que le volume ($V$) est réduit, a pression ($p$) augmente, et vice versa,

$p \propto \displaystyle\frac{1}{V}$



comme illustré dans le graphique suivant :



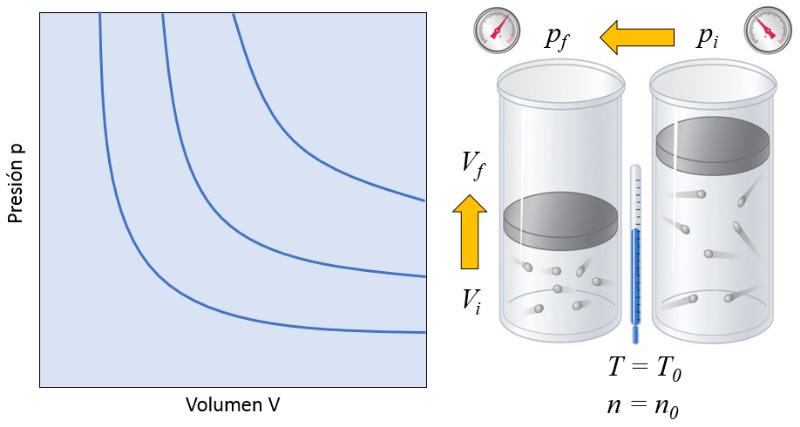
La relation entre le nombre de particules ($N$) et a température absolue ($T$) est que leur produit est égal à Une constante de la loi de Boyle ($C_b$), ce qui correspond à la loi de Boyle [1], en l'honneur de son découvreur Robert Boyle :

$ p V = C_b $

On parle parfois de la loi de Boyle-Mariotte, en souvenir du physicien français Edme Mariotte qui a découvert la même loi de manière indépendante en 1676. [1] "New Experiments Physico-Mechanical, Touching the Spring of the Air, and Its Effects" (Nouveaux essais physico-mécaniques, concernant la résilience de l'air et ses effets), Robert Boyle, Oxford : imprimé par H. Hall, imprimeur de l'université, pour Tho. Robinson (1660).

ID:(9531, 0)


Robert Boyle
Description

Robert Boyle était un scientifique irlandais né en 1627. Il est considéré comme l'un des fondateurs de la chimie moderne et est connu pour ses contributions dans le domaine du comportement des gaz. La relation entre Robert Boyle et la loi de Boyle vient du fait qu'il a formulé cette loi au XVIIe siècle. La loi de Boyle établit que, à température constante, le volume d'un gaz est inversement proportionnel à sa pression. Boyle a réalisé des expériences qui ont démontré cette relation et jeté les bases de la compréhension du comportement des gaz.

ID:(1657, 0)


Changement d'état d'un gaz parfait selon la loi de Boyle
Concept

La loi de Boyle stipule que, avec a température absolue ($T$) constant, le produit de a pression ($p$) et le volume ($V$) est égal à A constante de la loi de Boyle ($C_b$) :

$ p V = C_b $



Cela signifie que si un gaz passe d'un état initial (a pression à l'état initial ($p_i$) et le volume à l'état i ($V_i$)) à un état final (a pression à l'état final ($p_f$) et le volume à l'état f ($V_f$)), en maintenant a température absolue ($T$) constant, il doit toujours respecter la loi de Boyle :

$p_i V_i = C_b = p_f V_f$



Par conséquent, on a :

$ p_i V_i = p_f V_f $

ID:(15688, 0)


Équivalent à la loi de Boyle pour les densités
Concept

Si, dans un changement isotherme où le contenu ne varie pas, a pression à l'état initial ($p_i$), a pression à l'état final ($p_f$), le volume à l'état i ($V_i$) et le volume à l'état f ($V_f$) sont liés par :

$ p_i V_i = p_f V_f $



Alors, nous pouvons introduire a densité ($\rho$) qui, avec a masse ($M$) et le volume ($V$), satisfait :

$ \rho \equiv\displaystyle\frac{ M }{ V }$



Ce qui nous amène à A densité dans l'état i ($\rho_i$) et a densité dans l'état f ($\rho_f$) comme suit :

$\displaystyle\frac{ p_i }{ \rho_i } = \displaystyle\frac{ p_f }{ \rho_f }$

ID:(15687, 0)


Modèle
Concept


ID:(15313, 0)


Loi de Boyle-Mariotte
Modèle

La loi de Boyle-Mariotte établit que le produit de 5224 et 5226 d'un gaz reste constant lorsque la température absolue et la quantité de matière ne varient pas. Cela signifie que 5224 varie de manière inversement proportionnelle à 5226.

Variables
Symbole
Texte
Variable
Valeur
Unités
Calculer
Valor MKS
Unités MKS
$C_b$
C_b
Constante de la loi de Boyle
J
$\rho_f$
rho_f
Densité dans l'état f
kg/m^3
$\rho_i$
rho_i
Densité dans l'état i
kg/m^3
$M$
M
Masse
kg
$p_f$
p_f
Pression à l'état final
Pa
$p_i$
p_i
Pression à l'état initial
Pa
$V_f$
V_f
Volume à l'état f
m^3
$V_i$
V_i
Volume à l'état i
m^3

Calculs

D'abord, sélectionnez l'équation:   à ,  puis, sélectionnez la variable:   à 
Symbole
Équation
Résolu
Traduit

Calculs

Symbole
Équation
Résolu
Traduit

 Variable   Donnée   Calculer   Cible :   Équation   À utiliser


Équations

La loi de Boyle stipule que, avec a température absolue ($T$) constant, le produit de a pression ($p$) et le volume ($V$) est gal a constante de la loi de Boyle ($C_b$) :

$ p V = C_b $



Cela signifie que si un gaz passe d'un tat initial (a pression à l'état initial ($p_i$) et le volume à l'état i ($V_i$)) un tat final (a pression à l'état final ($p_f$) et le volume à l'état f ($V_f$)), en maintenant a température absolue ($T$) constant, il doit toujours respecter la loi de Boyle :

$p_i V_i = C_b = p_f V_f$



Par cons quent, on a :

$ p_i V_i = p_f V_f $

(ID 3491)

Si, dans un changement isotherme o le contenu ne varie pas, a pression à l'état initial ($p_i$), a pression à l'état final ($p_f$), le volume à l'état i ($V_i$) et le volume à l'état f ($V_f$) sont li s par :

$ p_i V_i = p_f V_f $



Alors, nous pouvons introduire a densité ($\rho$) qui, avec a masse ($M$) et le volume ($V$), satisfait :

$ \rho \equiv\displaystyle\frac{ M }{ V }$



Ce qui nous am ne a densité dans l'état i ($\rho_i$) et a densité dans l'état f ($\rho_f$) comme suit :

$\displaystyle\frac{ p_i }{ \rho_i } = \displaystyle\frac{ p_f }{ \rho_f }$

(ID 8834)

Exemples

La loi de Boyle-Mariotte, galement connue sous le nom de loi de Boyle, d crit la relation inverse entre la pression et le volume d'un gaz temp rature constante. Elle stipule que, pour une quantit fixe de gaz, lorsque la temp rature est maintenue constante, la pression du gaz augmente mesure que le volume diminue, et vice-versa. Cela signifie que si vous compressez un gaz en r duisant son volume, sa pression augmentera proportionnellement, et si vous augmentez le volume, la pression diminuera proportionnellement. Cette relation est fondamentale pour comprendre le comportement des gaz et s'exprime math matiquement par le produit de la pression et du volume tant une constante pour une quantit de gaz donn e temp rature constante.

(ID 15254)

A pression ($p$) est g n r lorsque les particules de gaz entrent en collision avec la surface du contenant de gaz. Comme a température absolue ($T$) est constant, l' nergie des particules ne varie pas et les chocs de celles-ci avec les surfaces du contenant de gaz ne varieront pas dans le transfert d'impulsion. Cependant, le nombre d'impacts d pend du nombre de particules pr s de la surface, qui son tour est proportionnel au a concentration de particules ($c_n$) du gaz.



D'autre part, la densit est inversement proportionnelle le volume ($V$), ce qui conduit la relation suivante :

$p \propto c_n \propto \displaystyle\frac{1}{V}$

(ID 9602)

Dans un gaz, si la fois a température absolue ($T$) et le nombre de particules ($N$) sont maintenus constants, on observe que le volume ($V$) et a pression ($p$) varient de mani re inversement proportionnelle. Chaque fois que le volume ($V$) est r duit, a pression ($p$) augmente, et vice versa,

$p \propto \displaystyle\frac{1}{V}$



comme illustr dans le graphique suivant :



La relation entre le nombre de particules ($N$) et a température absolue ($T$) est que leur produit est gal une constante de la loi de Boyle ($C_b$), ce qui correspond la loi de Boyle [1], en l'honneur de son d couvreur Robert Boyle :

$ p V = C_b $

On parle parfois de la loi de Boyle-Mariotte, en souvenir du physicien fran ais Edme Mariotte qui a d couvert la m me loi de mani re ind pendante en 1676. [1] "New Experiments Physico-Mechanical, Touching the Spring of the Air, and Its Effects" (Nouveaux essais physico-m caniques, concernant la r silience de l'air et ses effets), Robert Boyle, Oxford : imprim par H. Hall, imprimeur de l'universit , pour Tho. Robinson (1660).

(ID 9531)

Robert Boyle tait un scientifique irlandais n en 1627. Il est consid r comme l'un des fondateurs de la chimie moderne et est connu pour ses contributions dans le domaine du comportement des gaz. La relation entre Robert Boyle et la loi de Boyle vient du fait qu'il a formul cette loi au XVIIe si cle. La loi de Boyle tablit que, temp rature constante, le volume d'un gaz est inversement proportionnel sa pression. Boyle a r alis des exp riences qui ont d montr cette relation et jet les bases de la compr hension du comportement des gaz.

(ID 1657)

La loi de Boyle stipule que, avec a température absolue ($T$) constant, le produit de a pression ($p$) et le volume ($V$) est gal a constante de la loi de Boyle ($C_b$) :

$ p V = C_b $



Cela signifie que si un gaz passe d'un tat initial (a pression à l'état initial ($p_i$) et le volume à l'état i ($V_i$)) un tat final (a pression à l'état final ($p_f$) et le volume à l'état f ($V_f$)), en maintenant a température absolue ($T$) constant, il doit toujours respecter la loi de Boyle :

$p_i V_i = C_b = p_f V_f$



Par cons quent, on a :

$ p_i V_i = p_f V_f $

(ID 15688)

Si, dans un changement isotherme o le contenu ne varie pas, a pression à l'état initial ($p_i$), a pression à l'état final ($p_f$), le volume à l'état i ($V_i$) et le volume à l'état f ($V_f$) sont li s par :

$ p_i V_i = p_f V_f $



Alors, nous pouvons introduire a densité ($\rho$) qui, avec a masse ($M$) et le volume ($V$), satisfait :

$ \rho \equiv\displaystyle\frac{ M }{ V }$



Ce qui nous am ne a densité dans l'état i ($\rho_i$) et a densité dans l'état f ($\rho_f$) comme suit :

$\displaystyle\frac{ p_i }{ \rho_i } = \displaystyle\frac{ p_f }{ \rho_f }$

(ID 15687)


(ID 15313)

ID:(1472, 0)