Aterrizar
Storyboard 
La clave para aterrizar es modificar el ala de modo de lograr una sustentación suficiente a menor velocidad de modo de poder lograr controladamente alcanzar la pista y lograr detener el objeto en la pista disponible.
Variables
Cálculos
Cálculos
Ecuaciones
De forma similar a c mo se deriv la ecuaci n para la fuerza de sustentación ($F_L$) utilizando la densidad ($\rho$), el coeficiente de sustentación ($C_L$), la superficie que genera sustentación ($S_w$) y la velocidad respecto del medio ($v$)
en esta analog a, lo que corresponde a la superficie que genera sustentación ($S_w$) ser equivalente a el perfil total del objeto ($S_p$) y el coeficiente de sustentación ($C_L$) a el coeficiente de resistencia ($C_W$), con lo que se calcula la fuerza de resistencia ($F_W$):
El coeficiente de resistencia se mide y, en flujos turbulentos sobre cuerpos aerodin micos, generalmente se registran valores alrededor de 0.4.
Si igualamos la fuerza de propulsión ($F_p$) con la fuerza de resistencia ($F_W$) con el perfil total del objeto ($S_p$), el coeficiente de resistencia ($C_W$), la densidad ($\rho$) y la velocidad respecto del medio ($v$) en
obtenemos, para una la velocidad máxima ($v_p$),
$F_p = \displaystyle\frac{1}{2} \rho S_w C_L v_p ^2$
lo cual, al resolver para la velocidad m xima, resulta en
Con la aceleración máxima ($a_p$), expresada con la fuerza de propulsión ($F_p$) y la masa del cuerpo ($m$) se tiene
y la velocidad máxima ($v_p$) descrita con la densidad ($\rho$), la masa del cuerpo de la aeronave ($m_p$) y el coeficiente de resistencia ($C_W$) por
con ello podemos definir un el tiempo de propulsion de despegue/aterrizaje ($\tau_p$) utilizando la siguiente expresi n:
Utilizando la ecuaci n para la velocidad respecto del medio ($v$) en el tiempo de despegue ($t$) con la aceleración máxima ($a_p$) y la velocidad máxima ($v_p$):
puede integrarse desde un valor inicial de la velocidad de aterrizaje ($v_L$)
$\displaystyle\int_{v_L}^v \displaystyle\frac{dv}{1 - v^2/v_p^2} = -\displaystyle\int_0^t dt a_p$
y con la definici n de el tiempo de propulsion de despegue/aterrizaje ($\tau_p$)
obtenemos
Utilizando a equa o ERROR:6110,0 com la velocidad de aterrizaje ($v_L$), la velocidad máxima ($v_p$), el tiempo de propulsion de despegue/aterrizaje ($\tau_p$) e el tiempo de despegue ($t$) como segue:
onde em el tiempo de despegue ($t$) igual a el tiempo de aterrizaje ($t_L$), assim:
$v = v_L - v_p \tan\left(\displaystyle\frac{t_L}{\tau_p}\right)=0$
Se resolvermos esta equa o para o tempo, obtemos:
Dado que la velocidad respecto del medio ($v$) durante a aterragem varia em fun o de el tiempo de despegue ($t$) com la velocidad de aterrizaje ($v_L$), la velocidad máxima ($v_p$) e el tiempo de propulsion de despegue/aterrizaje ($\tau_p$) de acordo com a seguinte equa o:
igual a el camino recorrido en la pista ($s$) em rela o a el tiempo de despegue ($t$).
Podemos integrar a equa o:
$\displaystyle\frac{ds}{dt}=v_0-v_p\tan\left(\displaystyle\frac{t}{\tau_p}\right)$
Obtendo assim o caminho como:
$s = v_L t + \log(|\cos( t / \tau_p)|) v_p \tau_p$
Se el tiempo de despegue ($t$), o fator logar tmico pode ser desenvolvido at a terceira ordem, resultando em que o caminho de aterragem seja igual a:
Ejemplos
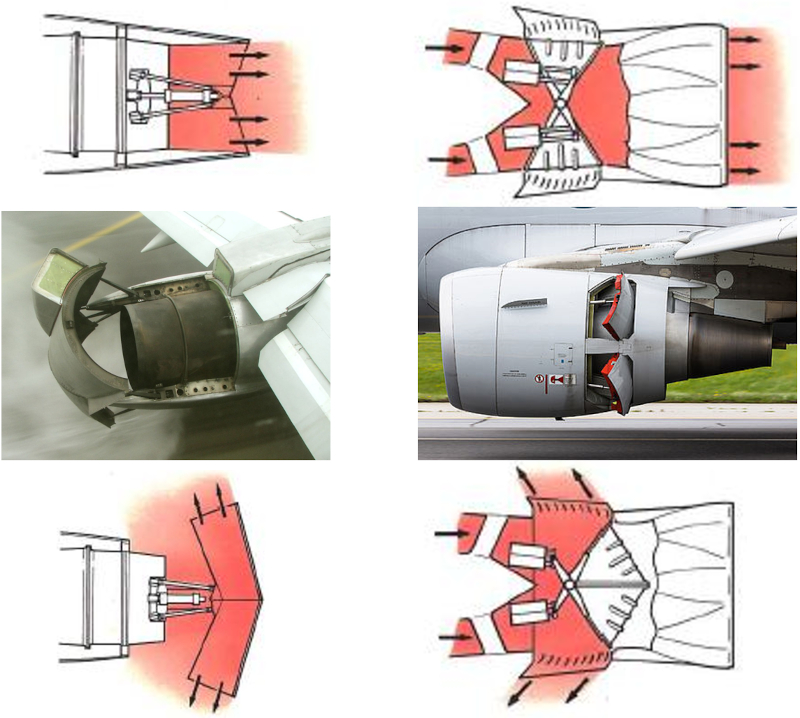
Los aviones utilizan tres mecanismos para frenar durante el aterrizaje:
• La reversi n del empuje, que consiste en redirigir el impulso de los motores hacia adelante en lugar de hacia atr s.
• Los spoilers en las alas, que aumentan el coeficiente de resistencia al exponer una superficie al flujo de aire.
• Los frenos convencionales en las ruedas.
En la imagen de abajo se muestran dos tipos de inversores de empuje: el primero utiliza un deflector que se mueve en el flujo de aire que sale del motor, mientras que el segundo desv a directamente el flujo hacia adelante.
La fuerza de resistencia ($F_W$) se puede calcular utilizando la densidad ($\rho$), el coeficiente de resistencia ($C_W$), el perfil total del objeto ($S_p$) y la velocidad respecto del medio ($v$) de acuerdo con la siguiente f rmula:
Al inicio del despegue, la resistencia aerodin mica, que depende de la velocidad, es m nima. Por lo tanto, la aceleración máxima ($a_p$) est determinada nicamente por la fuerza de propulsión ($F_p$) y la masa del cuerpo ($m$):
A medida que la resistencia comience a reducir la fuerza de propulsi n, esta aceleraci n inicial ser la m xima posible.
La fuerza de propulsión ($F_p$) contrarresta la fuerza de resistencia ($F_W$) generando velocidad, lo que a su vez aumenta la misma fuerza de resistencia, como se describe en el perfil total del objeto ($S_p$), el coeficiente de resistencia ($C_W$), la densidad ($\rho$) y la velocidad respecto del medio ($v$) en
Este proceso contin a aumentando la velocidad hasta el punto en el que la fuerza de propulsi n iguala a la fuerza de resistencia, lo que representa la velocidad m xima alcanzable.
Al igualar la fuerza de propulsi n con la fuerza de resistencia y resolver para la velocidad, obtenemos la velocidad máxima ($v_p$):
A medida que la resistencia comience a reducir la fuerza de propulsi n, esta aceleraci n inicial ser la m xima posible.
Con la aceleración máxima ($a_p$) generada por los motores y la velocidad máxima ($v_p$) podemos definir un el tiempo de propulsion de despegue/aterrizaje ($\tau_p$) utilizando la siguiente expresi n:
Este tiempo proporciona una estimaci n del orden de magnitud del proceso de despegue y aterrizaje, el cual generalmente se lleva a cabo en cuesti n de minutos.
La ecuaci n para calcular la velocidad respecto del medio ($v$) en el tiempo de despegue ($t$) con la aceleración máxima ($a_p$) y la velocidad máxima ($v_p$) es la siguiente:
Cuando se integra esta ecuaci n, se obtiene el resultado con el tiempo de propulsion de despegue/aterrizaje ($\tau_p$) y la velocidad de aterrizaje ($v_L$).
Al principio, cuando el tiempo es considerablemente menor que el tiempo caracter stico, es posible sustituir la tangente por su argumento. Esto implica que la velocidad disminuye principalmente debido a la influencia de los motores.
La ecuaci n de ERROR:6110,0 para un avi n durante el aterrizaje se expresa con la velocidad de aterrizaje ($v_L$), la velocidad máxima ($v_p$), el tiempo de propulsion de despegue/aterrizaje ($\tau_p$) y el tiempo de despegue ($t$) de la siguiente manera:
Por lo tanto, el tiempo de aterrizaje ($t_L$) se calcula utilizando esta ecuaci n para el caso en que la velocidad en ese momento es nula. Esto se traduce en:
Dado que la velocidad respecto del medio ($v$) durante el aterrizaje var a en funci n de el tiempo de despegue ($t$) con la velocidad de aterrizaje ($v_L$), la velocidad máxima ($v_p$) y el tiempo de propulsion de despegue/aterrizaje ($\tau_p$) de acuerdo con la ecuaci n:
podemos calcular la distancia recorrida a lo largo de la pista al integrar esta ecuaci n en el tiempo:
La ecuaci n resultante es una aproximaci n de tercer orden de $t/\tau_p$, lo que implica que las ayudas aerodin micas para el frenado son significativamente reducidas en comparaci n con la inversi n de los propulsores.
Adem s, podemos utilizar el tiempo de aterrizaje para estimar la longitud de pista necesaria para aterrizar.
El aterrizaje concluye cuando la velocidad respecto del medio ($v$) es nulo, lo que implica que el tiempo ($t$) es igual a el tiempo de aterrizaje ($t_L$), resultando en una reducci n de el camino recorrido en la pista ($s$) a el distancia de aterrizaje ($s_L$). Por lo tanto, con la aceleración máxima ($a_p$) y la velocidad de aterrizaje ($v_L$), se obtiene:
ID:(1968, 0)