Planear
Storyboard 
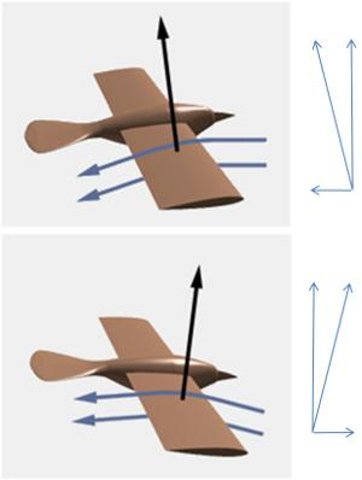
Si el objeto (avión/ave) mantiene un angulo de ataque levemente negativo, puede lograr que parte de la fuerza de sustentación contribuya a impulsar contrarrestando la resistencia. En la media de que la restante sustentación no sea mucho inferior a la fuerza de la gravedad se logra que el objeto se mantenga largamente en el aire. Se puede hablar de un descenso controlado extremadamente lento o planeo.
ID:(466, 0)
Planear
Storyboard 
Si el objeto (avión/ave) mantiene un angulo de ataque levemente negativo, puede lograr que parte de la fuerza de sustentación contribuya a impulsar contrarrestando la resistencia. En la media de que la restante sustentación no sea mucho inferior a la fuerza de la gravedad se logra que el objeto se mantenga largamente en el aire. Se puede hablar de un descenso controlado extremadamente lento o planeo.
Variables
Cálculos
Cálculos
Ecuaciones
La fuerza de sustentación ($F_L$), junto con la envergadura de las alas ($L$), la densidad ($\rho$), el factor de velocidad superior del ala ($c_t$), el factor de velocidad inferior del ala ($c_b$), la largo superior del ala ($l_t$), la largo inferior del ala ($l_b$) y la velocidad respecto del medio ($v$), se encuentra en
Si consideramos la superficie que genera sustentación ($S_w$), definido por la envergadura de las alas ($L$), la largo superior del ala ($l_t$) y la largo inferior del ala ($l_b$),
y para el coeficiente de sustentación ($C_L$), definido como
obtenemos
De forma similar a c mo se deriv la ecuaci n para la fuerza de sustentación ($F_L$) utilizando la densidad ($\rho$), el coeficiente de sustentación ($C_L$), la superficie que genera sustentación ($S_w$) y la velocidad respecto del medio ($v$)
en esta analog a, lo que corresponde a la superficie que genera sustentación ($S_w$) ser equivalente a el perfil total del objeto ($S_p$) y el coeficiente de sustentación ($C_L$) a el coeficiente de resistencia ($C_W$), con lo que se calcula la fuerza de resistencia ($F_W$):
El coeficiente de resistencia se mide y, en flujos turbulentos sobre cuerpos aerodin micos, generalmente se registran valores alrededor de 0.4.
Si consideramos la fuerza de sustentación ($F_L$), la fuerza de resistencia ($F_W$), la masa del cuerpo ($m$), la aceleración gravitacional ($g$) y el ángulo de planeo ($\phi$), la fuerza en el planeo en la direcci n vertical es:
y en la direcci n horizontal es:
lo que nos permite eliminar la fuerza de resistencia ($F_W$), resultando en:
$F_L=F_W\displaystyle\frac{\cos\phi}{\sin\phi} \rightarrow F_W(\sin^2\phi+\cos^2\phi)=mg\sin\phi$
Por lo tanto, la fuerza de sustentación ($F_L$) es:
Si consideramos la fuerza de sustentación ($F_L$), la fuerza de resistencia ($F_W$), la masa del cuerpo ($m$), la aceleración gravitacional ($g$) y el ángulo de planeo ($\phi$), la fuerza durante el planeo en la direcci n vertical es:
y en la direcci n horizontal es:
lo que nos permite eliminar la fuerza de sustentación ($F_L$), resultando en:
$F_L=F_W\displaystyle\frac{\cos\phi}{\sin\phi} \rightarrow F_W(\sin^2\phi+\cos^2\phi)=mg\sin\phi$
Entonces, la fuerza de resistencia ($F_W$) debe ser:
Consideremos la fuerza de sustentación ($F_L$), la fuerza de resistencia ($F_W$), la masa del cuerpo ($m$), la aceleración gravitacional ($g$) y el ángulo de planeo ($\phi$). Con estas fuerzas, la fuerza de sustentaci n se calcula como:
y la resistencia como:
Podemos determinar el ángulo de planeo ($\phi$) dividiendo la fuerza de sustentación ($F_L$) por la fuerza de resistencia ($F_W$), lo que resulta en:
$\tan\phi=\displaystyle\frac{F_W}{F_L}$
Donde la fuerza de resistencia ($F_W$) se calcula utilizando la ecuaci n:
con el perfil total del objeto ($S_p$) y el coeficiente de resistencia ($C_W$). De manera similar, la fuerza de sustentación ($F_L$) se calcula como:
con la superficie que genera sustentación ($S_w$) y el coeficiente de sustentación ($C_L$).
Con ambas fuerzas, podemos determinar el ngulo de ataque necesario para planear como:
Ejemplos
Una t cnica de vuelo es conocida como planeo. En esta t cnica, se utilizan las alas tanto para propulsarse como para mantenerse en el aire. Para lograrlo, es esencial ajustar el ngulo de ataque del ala de manera que la fuerza de sustentaci n compense la fuerza gravitatoria. En consecuencia, el planeo se convierte en un descenso controlado en el que se aprovecha la ca da para generar sustentaci n y, de esta manera, reducir la velocidad de forma controlada.
La clave para el planeo es inclinar el avi n o ave hacia adelante, es decir, tener un ngulo negativo representado por ERROR:6121,0. Con este ngulo negativo, el vector de la fuerza de sustentación ($F_L$) apunta hacia arriba y hacia adelante en lugar de hacia atr s. Esto da como resultado una fuerza de tracci n en lugar de la fuerza de resistencia ($F_W$), lo que impulsa al avi n o ave y genera velocidad, y a su vez, crea la sustentaci n necesaria.
Este mecanismo permite volar, pero es esencial entender que es una especie de ca da lenta y controlada, ya que no se logra un una fuerza de sustentación ($F_L$) vertical que contrarreste completamente el propio peso. Por lo tanto, es necesario llevar el planeador a altitudes elevadas o permitir que el ave gane altura inicialmente mediante su propia propulsi n. Luego, ambos buscan corrientes ascendentes que les permiten planear dentro de una corriente ascendente que es m s fuerte que la velocidad de descenso del planeador. De esta manera, pueden mantenerse en vuelo durante largos per odos de tiempo sin necesidad de aterrizar.
De manera similar a la definici n de el angulo de ataque del ala ($\alpha$) como el ngulo entre la l nea media del ala y el horizonte, se puede establecer su contraparte en el rango negativo, que se conoce como el ángulo de planeo ($\phi$).
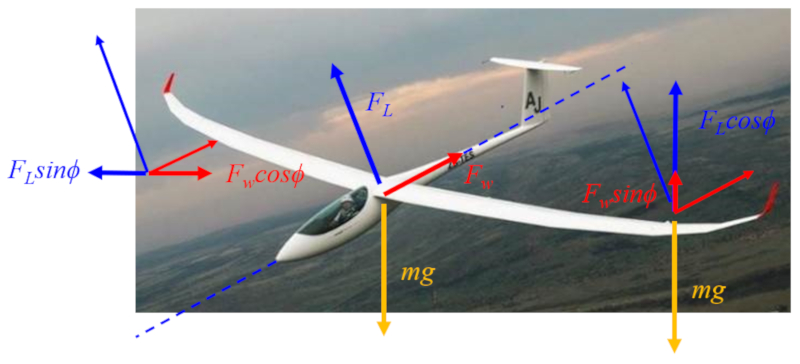
En el caso de las fuerzas, tenemos las siguientes acciones:
• la fuerza de sustentación ($F_L$) act a perpendicularmente al eje del avi n o ave.
• la fuerza de resistencia ($F_W$) act a a lo largo del eje del avi n o ave.
• la fuerza gravitacional ($F_g$) ($mg$) act a verticalmente.
Estas tres fuerzas se representan en el centro del diagrama:
En el lado izquierdo, se observa la componente horizontal, donde la sustentaci n contrarresta la resistencia, actuando como impulso.
En el lado derecho, se observan las componentes verticales, donde ambas fuerzas aerodin micas (sustentaci n y resistencia) se oponen al peso que act a sobre el centro de masa.
Aunque las fuerzas se equilibran entre s , el planeador desciende debido a que su direcci n de vuelo est determinada por el ngulo de planeo.
El angulo de planeo es aquel angulo de inclinaci n en que la componente horizontal de la fuerza de tracci n contrarresta horizontal de roce mientras que la suma de las de sustentaci n y roce en direcci n vertical contrarrestan la fuerza de gravedad. Esta situaci n permite un descenso con un angulo igual al angulo de planeo que puede ser peque o permitiendo un descenso muy lento.
Si consideramos la fuerza de sustentación ($F_L$), la fuerza de resistencia ($F_W$), la masa del cuerpo ($m$), la aceleración gravitacional ($g$) y el ángulo de planeo ($\phi$), la fuerza durante el planeo en la direcci n vertical es:
y en la direcci n horizontal es:
lo que nos permite eliminar la fuerza de sustentación ($F_L$), resultando en:
$F_L=F_W\displaystyle\frac{\cos\phi}{\sin\phi} \rightarrow F_W(\sin^2\phi+\cos^2\phi)=mg\sin\phi$
Entonces, la fuerza de resistencia ($F_W$) debe ser:
Si consideramos la fuerza de sustentación ($F_L$), la fuerza de resistencia ($F_W$), la masa del cuerpo ($m$), la aceleración gravitacional ($g$) y el ángulo de planeo ($\phi$), la fuerza en el planeo en la direcci n vertical es:
y en la direcci n horizontal es:
lo que nos permite eliminar la fuerza de resistencia ($F_W$), resultando en:
$F_L=F_W\displaystyle\frac{\cos\phi}{\sin\phi} \rightarrow F_W(\sin^2\phi+\cos^2\phi)=mg\sin\phi$
Por lo tanto, la fuerza de sustentación ($F_L$) es:
Consideremos la fuerza de sustentación ($F_L$), la fuerza de resistencia ($F_W$), la masa del cuerpo ($m$), la aceleración gravitacional ($g$) y el ángulo de planeo ($\phi$). Con estas fuerzas, la fuerza de sustentaci n se calcula como:
y la resistencia como:
Podemos determinar el ángulo de planeo ($\phi$) dividiendo la fuerza de sustentación ($F_L$) por la fuerza de resistencia ($F_W$), lo que resulta en:
$\tan\phi=\displaystyle\frac{F_W}{F_L}$
Donde la fuerza de resistencia ($F_W$) se calcula utilizando la ecuaci n:
con el perfil total del objeto ($S_p$) y el coeficiente de resistencia ($C_W$). De manera similar, la fuerza de sustentación ($F_L$) se calcula como:
con la superficie que genera sustentación ($S_w$) y el coeficiente de sustentación ($C_L$).
Con ambas fuerzas, podemos determinar el ngulo de ataque necesario para planear como:
En el caso del planeo, el objetivo es mantener una velocidad constante, por lo que la fuerza de sustentación ($F_L$) debe generar suficiente propulsi n para contrarrestar la fuerza de resistencia ($F_W$).
Para lograr esta ERROR:6120,0, el ave o aeronave genera un un angulo de ataque del ala ($\alpha$) negativo, lo que significa que parte de la fuerza de sustentación ($F_L$) se convierte en fuerza de propulsi n. Esta componente de fuerza es igual al seno del ngulo.
La inclinaci n tambi n conduce a una reducci n en la fuerza de resistencia ($F_W$), ya que una parte de esta contribuye a la sustentaci n. En este caso, la componente que a n contribuye a la resistencia es esta fuerza multiplicada por el coseno del ngulo.
Por lo tanto, la ecuaci n de fuerza en el plano horizontal se puede expresar como:
En lugar de utilizar el angulo de ataque del ala ($\alpha$), trabajaremos con el ángulo de planeo ($\phi$).
En el plano vertical, el ángulo de planeo ($\phi$) provoca una reducci n en la fuerza de sustentación ($F_L$) por un factor igual al coseno del ngulo. Por otro lado, hace que la fuerza de resistencia ($F_W$) contribuya a la sustentaci n con un factor igual al seno del ngulo. Ambas fuerzas deben contrarrestar el peso generado por la masa del cuerpo ($m$) y la aceleración gravitacional ($g$), por lo que obtenemos:
La fuerza de sustentación ($F_L$) es con la masa del cuerpo ($m$), la aceleración gravitacional ($g$) y el ángulo de planeo ($\phi$) igual a:
La fuerza de resistencia ($F_W$) es con la masa del cuerpo ($m$), la aceleración gravitacional ($g$) y el ángulo de planeo ($\phi$) igual a:
La fuerza de sustentación ($F_L$) y la fuerza de resistencia ($F_W$) dependen de la masa del cuerpo ($m$), la aceleración gravitacional ($g$), y el ángulo de planeo ($\phi$). Ambas ecuaciones nos permiten calcular el ángulo de planeo ($\phi$) en t rminos de la fuerza de sustentación ($F_L$) y la fuerza de resistencia ($F_W$).
Dado que la fuerza de sustentación ($F_L$) y la fuerza de resistencia ($F_W$) son funciones de la masa del cuerpo ($m$), la velocidad respecto del medio ($v$), la superficie que genera sustentación ($S_w$), el perfil total del objeto ($S_p$), el coeficiente de sustentación ($C_L$) y el coeficiente de resistencia ($C_W$), podemos mostrar que el ángulo de planeo ($\phi$) es:
Para crear una presi n mayor debajo que encima del ala y generar sustentaci n, se emplea la Ley de Bernoulli, corrigiendo la falta de conservaci n de la densidad de energ a mediante un coeficiente de sustentación ($C_L$). La presi n sobre el ala, la fuerza de sustentación ($F_L$), se puede estimar utilizando la densidad ($\rho$), la superficie que genera sustentación ($S_w$), el coeficiente de sustentación ($C_L$) y la velocidad respecto del medio ($v$) mediante la siguiente f rmula:
La fuerza de resistencia ($F_W$) se puede calcular utilizando la densidad ($\rho$), el coeficiente de resistencia ($C_W$), el perfil total del objeto ($S_p$) y la velocidad respecto del medio ($v$) de acuerdo con la siguiente f rmula:
ID:(466, 0)